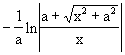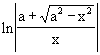Intégrales contenant des fonctions irrationnelles
Analyse
NB : on omet la constante d'intégration c.
| ∫ |
1 / |
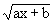 |
dx = (2/a)ˇ |
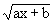 |
| ∫ |
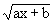 |
dx = |
(2/3a)ˇ |
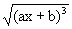 |
| ∫ |
1 / |
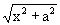 |
dx = |
ln |x + |
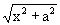 |
| |
| ∫ |
x / |
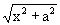 |
dx = |
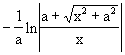 |
= |
-(1/a)ˇ
arcsinh (a/x) |
| ∫ |
1 / (x2ˇ
|
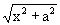 |
)dx = - |
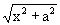 |
/ (a2x) |
| ∫ |
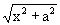 |
dx = |
(x/2)ˇ |
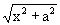 |
+ (a2/2)ˇ
ln |x + |
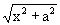 |
| |
| ∫ |
xˇ |
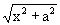 |
dx = (1/3)ˇ
(x2 + a2)ˇ
|
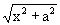 |
Quand |x| > a :
| ∫ |
1 / |
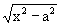 |
dx = ln |x + |
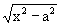 |
| |
| ∫ |
x / |
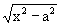 |
dx = |
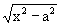 |
| ∫ |
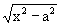 |
dx = (x/2)ˇ |
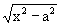 |
- (a2/2)ˇ
ln |x + |
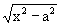 |
| |
| ∫ |
xˇ |
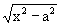 |
dx = |
(1/3)ˇ
(x2 - a2)ˇ
|
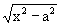 |
Quand |x| < a
| ∫ |
1 / |
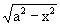 |
dx = arcsin (x/a) |
| ∫ |
x / |
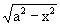 |
dx = - |
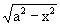 |
| ∫ |
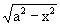 |
dx = (x/2)ˇ |
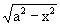 |
+ (a2/2)ˇ
arcsin (x/a) |
| ∫ |
xˇ |
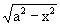 |
dx = |
-(1/3)ˇ
(a2 - x2)ˇ
|
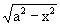 |
Recherche personnalisée