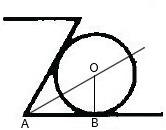
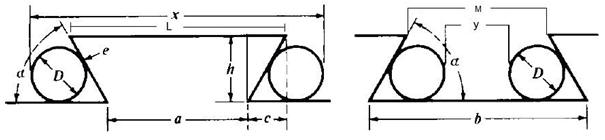
Measuring Dovetail Slides / Mesure des queues d'aronde

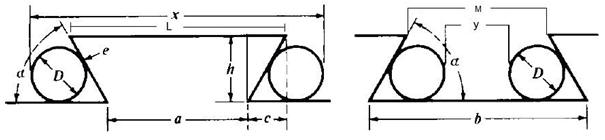
| E = AB | D = b - y - 2E | L = a + 2c |
| R = OB | D = ( b - y ) / (1 + 1/tan(α/2)) | L = a + (2h / tanα) |
| R = D / 2 | D = x - a - 2E | L = a + (2h ; tan(α/2)) |
| R = E ; tan (α/2) | D = (x - a) / (1 + 1/tan(α/2)) | L = x + (2h ; tan(α/2)) - (D / tan(α/2)) - D |
| L = x + 2c - 2E - D | ||
| a = L - 2c | L = x + (2h ; tan(α/2)) - 2E - D | |
| a = L - 2h ; tan(α/2) | E = R / tan(α/2) | |
| a = L - 2h/ tanα | E = (b - y - D) / 2 | M = b - 2c |
| a = x - 2E - D | E = (x - a - D) / 2 | M = (y + D(1 + 1/tan(α/2)) - 2c |
| a = x - D(1 + 1/tan(α/2)) | E = (x - L - D + 2c) / 2 | M = b - (2h ; tan(α/2)) |
| E = (x - L -D +(2h ; tan(α/2))) /2 | ||
| b = y + D(1 + 1/tan(α/2)) | h = c / tan(α/2) | x = a + 2E + D |
| b = M + 2c | h = c ; tanα | x = a + D(1 + 1/tan(α/2)) |
| b = M + 2h;tan(α/2) | h = (L-a) / 2tan(α/2) | x = L - (2h ; tan(α/2)) + D/tan(α/2) + D |
| b = 2E + y + D | h = ((L-a) ; tanα) / 2 | x = L - 2c + 2E + D |
| h = (b - M) / 2tan(α/2) | x = L - (2h ; tan(α/2)) + 2E + D | |
| c = h / tanα | h = ((b-M) ; tanα) / 2 | |
| c = h ; tan(α/2) | y = b – (D ; (1 + 1/tan(α/2))) | |
| c = (L-a) / 2 | y = b - 2E -D | |
| c = (L - x + 2E + D) / 2 | y = (M + 2c) – (D ; (1 + 1/tan(α/2))) | |
| c = (b - M) / 2 | ||
| c = (y + (D ; (1 + 1/tan(α/2)) - M) / 2 | ||
| tan(α/2) = R / E | tan(α/2) = 1 / (((x - a) / D) -1) | |
| tan(α/2) = c / h | tan(α/2) = 1 / (((b-y) / D) -1) | |
| tanα = h / c | tan(α/2) = (x - L) | tan(α/2) = 1 / (((M + 2c - y) / D) - 1) |
| tanα = 2h / (L-a) | tan(α/2) = (b - M) / 2h | tan(α/2) = (2E - x + L + D) / 2h |
| tanα = 2h / (b-M) | tan(α/2) = (L-a) / 2h |
