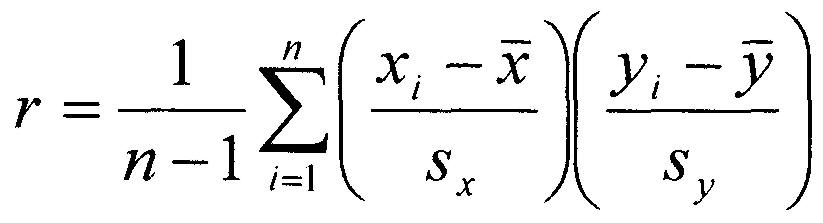
Meilleur ajustement de Lignes

Lorsqu'ils examinent des données par paires ordonnées, les statisticiens réalisent fréquemment des nuages ​​de points, ou représentations graphiques des paires de données sur le plan des coordonnées. Ils peuvent ainsi mesurer la force et la direction de l'association linéaire des points de données en calculant une valeur appelée coefficient de corrélation d'échantillon, représentée symboliquement par r.

De plus, les statisticiens peuvent construire des droites de meilleur ajustement, également appelées droites de régression des moindres carrés (ces droites étant obtenues en minimisant la somme des carrés des erreurs), afin de modéliser linéairement les tendances.

Comme dans une grande partie des statistiques, les calculs nécessaires à la création de droites de meilleur ajustement sont, sans surprise, confiés à une calculatrice ou à un ordinateur. (C'est pourquoi les statistiques ont connu un essor considérable depuis l'avènement de la puissance de calcul accessible.)

Avant de présenter LINE.BAS, un programme qui construit et affiche des droites de meilleur ajustement à l'écran, examinons quelques-unes des formules qui sous-tendent ces calculs.

Tout d'abord, il y a le coefficient de corrélation, r, qui mesure la force et la direction de l'association linéaire de l'ensemble de données appariées.

Si un nuage de points des données présente une pente positive (de gauche à droite), alors la direction est positive et r aura un signe positif. De même, si la tendance des données est négative (de gauche à droite), alors la direction est négative et r aura un signe négatif.

Si les points de données se trouvent tous sur une droite horizontale, alors le coefficient de corrélation sera 0.

Le calcul du coefficient de corrélation est obtenu en additionnant les produits de deux scores z, puis en divisant cette somme par un de moins que le nombre de points de données appariés.

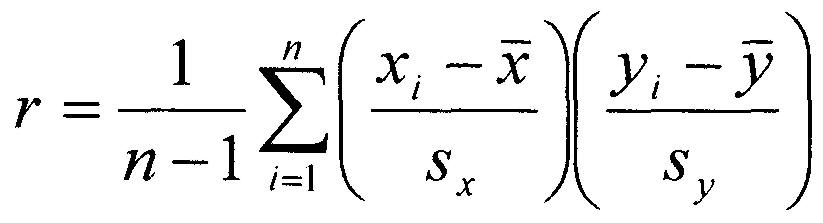
Un score z, également appelé score standardisé, indique le nombre d'écarts types par rapport à la moyenne d'une observation donnée.

Pour calculer un score z, il faut d'abord déterminer la moyenne (la moyenne arithmétique ordinaire) et l'écart type (la distance typique entre les points de données et la moyenne). Comme le montre la formule ci-dessus, un algorithme permettant de trouver la moyenne (les lettres barrées) et l'écart type (les s avec les indices de x et y) des x et des y doit être implémenté avant de calculer r.

Une fois le coefficient de corrélation calculé, la droite d'ajustement optimal est à portée de main. Une équation linéaire à deux variables, x et y, comporte deux parties : l'ordonnée à l'origine (l'ordonnée à l'intersection de la droite avec l'axe des y) et la pente (la variation de y pour chaque variation d'une unité de x). L'équation générale d'une droite d'ajustement optimal est la suivante :

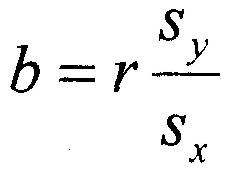
Et la formule de l'ordonnée à l'origine est

Pour trouver la droite d'ajustement optimal, il faut d'abord saisir quelques points. Au lieu de saisir les coordonnées, le programme LINE.BAS vous permet de déplacer le curseur pour dessiner les points (en appuyant sur la barre d'espace).

Une fois satisfait, appuyez sur la lettre L pour ajuster une droite aux données, la dessiner à l'écran et afficher l'équation. Mieux encore, vous pouvez ajouter d'autres points de données et tracer une autre droite, d'une couleur différente, ce qui vous permet d'explorer l'impact des paires de coordonnées supplémentaires sur les droites d'ajustement optimal.

Une variable INKEY$ gère toutes les saisies au clavier lors du tracé des paires de coordonnées ; lorsque la touche L est enfoncée, le programme renvoie l'interpréteur à la ligne 210, point de départ des nombreux calculs nécessaires pour trouver la droite d'ajustement optimal (comme décrit ci-dessus).

La droite d'ajustement optimal et le coefficient de corrélation sont communiqués à l'utilisateur, correctement formatés à l'aide d'une instruction PRINT USING (voir lignes 480 à 525). La droite d'ajustement optimal est ensuite tracée à l'écran (voir lignes 530 à 590).

Le programme présente plusieurs limitations.

Premièrement, vous ne pouvez tracer que des points dans le premier quadrant, ce qui signifie que vos x et y doivent être positifs.

En fait, vous n'êtes même pas autorisé à tracer des points sur l'un ou l'autre des axes ! (Cela s'explique en grande partie par le fait que le déplacement du curseur sur les axes les « coupe », un problème que nous aborderons dans le prochain chapitre du programme.)

Deuxièmement, une fois un point tracé, il est impossible de le supprimer. Ce manque de flexibilité entrave toute découverte statistique personnelle.

Troisièmement, supposons que vous soyez paresseux ou fatigué et que vous souhaitiez simplement saisir les paires de coordonnées via le pavé numérique, plutôt que de tracer les points. Il n'existe aucune option pour le faire.

Enfin, des notions statistiques plus avancées, telles que la régression non linéaire (par exemple, les courbes de meilleur ajustement) et la régression multiple (c'est-à-dire les équations de meilleur ajustement avec plusieurs variables x), pourraient trouver leur place dans un programme LINE.BAS bien plus complet.

LINE.BAS

10 KEY OFF:SCREEN 7:COLOR 15,0:CLS
20 DIM XXX(100):DIM YYY(100) 'Arrays for points
25 C=10 'Starting line colon
30 PRINT"PLOT THE POINTS OF YOUR DATA SET"
40 PRINT"MOVE LEFT, RIGHT, UP, DOWN WITH A,S,W,Z"
50 PRINT"PLOT POINT WITH THE <SPACE> "
60 PRINT"PRESS L TO SEE THE LINE, <ESC> TO QUIT"
70 LINE (30,35)-(30,200),15
80 LINE (20,190)-(350,190),15
85 X=32:Y=188 'Starting values for point
86 XX=2:YY=2 'Starting values for coordinates
87 ELEMENT=1 'Counting array elements
90 I$=INKEY$
100 PSET(X,Y),15
105 LOCATE 6,25:PRINT"(";XX;",";YY;")"
110 IF I$="" THEN 90
115 PRESET(X,Y),0
120 IF I$=CHR$(27) THEN END
130 IF I$="A" OR I$="a" THEN X=X-1:XX=XX-1
140 IF I$="S" OR I$="s" THEN X=X+1:XX=XX+1
150 IF I$="W" OR I$="w" THEN Y=Y-1:YY=YY+1
160 IF I$="Z" OR I$="z" THEN Y=Y+1:YY=YY-1
165 IF I$=" " THEN XXX(ELEMENT)=XX:YYY(ELEMENT)=YY:ELEMENT=ELEMENT+1:PSET(X,Y),10:X=X+1-Y=Y-1:XX=XX+1:YY=YY+1
170 IF X=30 THEN X=31:XX=1
171 IF X=301 THEN X=300:XX=270
172 IF Y=190 THEN Y=189:YY=1
173 IF Y=48 THEN Y=49:YY=140
182 IF ELEMENT>100 THEN ELEMENT=100 'overwrite on previous elements if necessary
190 IF I$="L" OR I$="l" THEN GOTO 210
200 GOTO 90
210 'Find the line of best fit
215 SUMX=0:SUMY=0:MEANX=0:MEANY=0:SSX=0:SSY=0:SDX=0:SDY=0:ZSCOREX=0:ZSCOREY=0:PRODUCT=0:SLOPE=0:YINT=0
220 'First, find the mean of the x and y values
230 FOR A=1 TO ELEMENT-1
240 SUMX=SUMX+XXX(A)
250 SUMY=SUMY+YYY(A)
260 NEXT A
270 MEANX=SUMX/(ELEMENT-1)
280 MEANY=SUMY/(ELEMENT-1)
300 'Next, find the standard deviation of the x and y values
310 FOR B=1 TO ELEMENT-1
320 SSX=SSX+(XXX(B)-MEANX)^2
330 SSY=SSY+(YYY(B)-MEANY)^2
340 NEXT B
350 SDX=SQR(SSX/(ELEMENT-2)):SDY=SQR(SSY/(ELEMENT-2))
360 'Next, find the correlation coefficient of x and y
370 FOR C=1 TO ELEMENT-1
380 IF SDX=0 THEN ZSCOREX=0 ELSE ZSCOREX=(XXX(C)-MEANX)/SDX
390 IF SDY=0 THEN ZSCOREY=0 ELSE ZSCOREY=(YYY(C)-MEANY)/SDY
400 PRODUCT=PRODUCT+ZSCOREX*ZSCOREY
410 NEXT C
420 R=PRODUCT/(ELEMENT-2)
430 'Find the equation of the line of best fit 440 "First, find the slope
450 IF SDX=0 THEN SLOPE=0 ELSE SLOPE=R*SDY/SDX
460 'Next, find the y-intercept
470 YINT=MEANY-SLOPE*MEANX
480 'Output the equation on-screen
485 'Use PRINT USING to format output nicely
490 LOCATE 7,18
500 IF SLOPE>0 THEN PRINT"y=";:PRINT USING"####.##";YINT;:PRINT"+";:PRINT USING"####.##";SLOPE;:PRINT"x"
510 IF SLOPE<0 THEN PRINT"y=";:PRINT USING"####.##";YINT;:PRINT USING"####.##";SLOPE;:PRINT"x'
520 IF SLOPE=0 THEN PRINT"y=";:PRINT USING"####.##";YINT
525 LOCATE 8,18:PRINT"r=";:PRINT USING"#.###";R
530 'Draw the line on-screen
531 IF C>14 THEN C=10
532 C=C+1 'Cycle through different colors for line of best fit
535 PSET(30,190-YINT),C
536 MOVE=190-YINT
540 FOR LOOP=31 TO 300
541 IF SLOPE>0 THEN MOVE=MOVE-SLOPE
542 IF SLOPE<0 THEN MOVE=MOVE-SLOPE
543 IF SLOPE=0 THEN MOVE=MOVE+SLOPE
544 LINE -(LOOP,MOVE),C
545 NEXT LOOP
588 FOR D=1 TO ELEMENT-1
585 PSET(XXX(D)+30,190-YYY(D)),16
590 NEXT D
600 GOTO 90