Tension induite dans un conducteur
PRINCIPE III DE L'ÉLECTROMAGNÉTISME
En 1831, Michael Faraday découvrit par hasard un des phénomènes les plus importants de l' électromagnétisme.
Ce phénomène, nommé loi de l'induction électromagnétique de Faraday, énonce le processus fondamental de l'induction d'une tension dans un circuit.
Pour en faciliter l'étude, nous avons séparé arbitrairement la loi de Faraday en deux parties appelées respectivement principe III et principe IV de l'électromagnétisme.
Le principe III étudié dans cette section porte sur l'induction d'une tension dans un conducteur mobile; le principe IV que nous étudierons à la section Induction électromagnétique concerne l'induction généralisée d'une tension.
Tension induite dans un conducteur
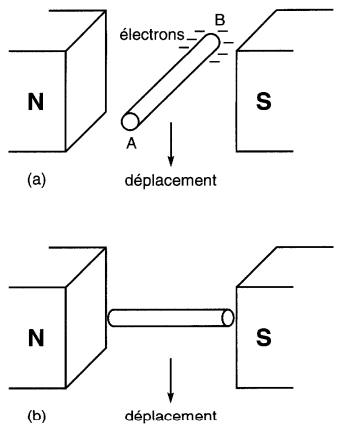
Selon le principe III de l'électromagnétisme, lorsqu'on déplace un conducteur dans un champ magnétique de façon à «couper» des lignes de force, il apparaît une différence de potentiel entre ses extrémités.
On dit alors qu'une tension est induite dans le conducteur. C'est sur ce principe que fonctionnent les dynamos et les alternateurs qui transforment l'énergie mécanique en énergie électrique. Afin de mieux comprendre le phénomène, considérons un conducteur en mouvement entre les deux pôles d'un aimant permanent (Fig. 17-1).
Figure 17-1 Induction d'une tension dans un conducteur en mouvement :
a. La tension induite est maximale lorsque le conducteur est perpendiculaire au flux;
b. La tension induite est nulle lorsque le conducteur en mouvement est parallèle au flux
On peut démontrer expérimentalement que :
1. Si le conducteur est perpendiculaire aux lignes de force (Fig. 17-1 a), et s'il est déplacé vers le bas, les électrons libres du conducteur sont chassés de l'extrémité A vers B et, par conséquent, il apparaît une différence de potentiel entre A et B.
2. Cette différence de potentiel, ou tension, disparaît dès que le déplacement cesse.
3. Si le conducteur est parallèle aux lignes de force (Fig. 17-lb), il n'apparaît aucune tension lorsqu'il est déplacé.
On est donc amené à conclure qu'une tension est développée seulement quand les lignes de force sont «coups» par le conducteur.
Ainsi, dans la Fig. 17-1b, il n' a aucune ligne de coupée et, par suite, aucune tension. La tension induite est de même nature que celle qui existe entre les bornes d'une pile. Nous disposons donc, pour la première fois, d'un moyen mécanique pour produire une tension.
Valeur de la tension induite
La valeur de la tension induite dans un conducteur dépend uniquement du nombre de lignes coupées par seconde. Par définition, lorsque le flux est coupé à un taux de 1 weber par seconde, une tension de 1 volt apparaît i est induite) entre les extrémités du conducteur.
Chose remarquable, la valeur de la tension induite ne dépend ni de la forme du conducteur, ni de la forme du champ magnétique. Une tension de 1 volt sera toujours induite entre les extrémités d'un conducteur, pourvu qu'il coupe les lignes à un taux de 1 weber par seconde.
De même, si un conducteur de forme tordue coupe un champ magnétique à raison de 2 webers par seconde, une tension de 2 volts est induite entre ses deux extrémités (Fig. 17-2).
Figure 17-2 Positions successives d'un conducteur de forme tordue coupant de façon aléatoire un champ magnétique quelconque.
Si le conducteur coupe les lignes à raison de 2 Wb/s, une tension de 2 V sera induite entre ses extrémités. La nature aléatoire du déplacement et de la densité de flux n'affecte pas la valeur de la tension.
Notons que le mouvement du conducteur par rapport au champ magnétique est relatif: un conducteur stationnaire peut être coupé par un champ qui se déplace. En somme, la valeur de la tension induite dépend seulement du flux coupé par seconde, quel que soit le moyen utilisé.
C'est ce qu'exprime la formule :
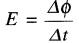(17-1)
où
Exemple 17-1
Lin aimant permanent ayant une section de 100 cm2 produit une densité de flux de 0.5 tesla entre ses pôles (Fig. 17-3).
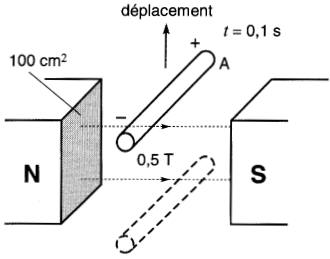
Calculer la tension induite entre les extrémités d'un conducteur traversant le champ en 0, I seconde.
Solution
Le flux coupé vaut:
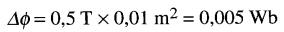
d'où la tension induite:
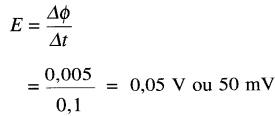
Même pour un aimant puissant et un déplacement rapide, la tension induite demeure faible, ce qui explique peut-être pourquoi le principe de l'induction ne fut pas découvert plus tôt.
Tension induite dans un conducteur rectiligne
Si un conducteur rectiligne coupe les lignes de flux à angle droit, on constate que la valeur de la tension induite est proportionnelle à:
1. la longueur du conducteur
2. la densité de flux
3. la vitesse du déplacement
C'est ce qu'exprime la formule:
E = Blv (17-2)
où
E = tension induite, en
volts [V]
B = densité de flux, en teslas [T]
l = longueur du conducteur dans le champ, en mètres [m]
v = vitesse de déplacement, en mètres par seconde [m/s]
Exemple 17-2
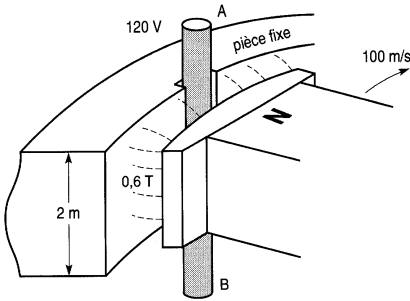
Les conducteurs d'une grosse génératrice ont une longueur de 2 mètres et ils sont coupés par un champ de 0.66 tesla qui se déplace à 100 mètres par seconde (Fig. 17-4). Calculer la valeur de la tension induite dans chaque conducteur.
Figure 17-4 Tension induite dans les conducteurs d'une génératrice (exemple 17-2)
Solution
D'après la formule 17-2, on obtient :
E=Blv = 0,6T x 2m x 100m/s =120V
Polarité de la tension induite
Considérons le conducteur de la Fig. 17-5.
Figure 17-5 La polarité de la tension induite dépend de la direction du déplacement
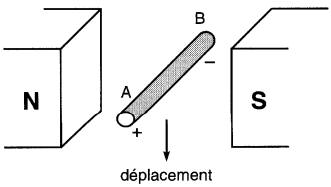
On trouve expérimentalement que si le conducteur est déplacé vers le bas, l'extrémité A du conducteur est positive (+) par rapport à l'extrémité B. Par contre, si le conducteur est déplacé vers le haut, l'extrémité B devient positive par rapport à A.
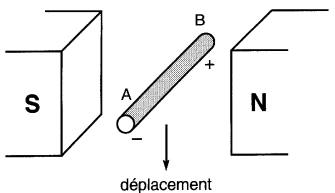
Enfin, si le sens des lignes de force est inversé (Fig. 17-6), on obtient les résultats inverses. On en conclut que la polarité de la tension induite dépend à la fois du sens du déplacement et du sens des lignes de force.
Figure 17-6 La polarité de la tension induite dépend de la direction du flux.
On peut trouver la polarité de la tension induite en se servant d'une règle simple, appelée règle des trois doigts de Fleming.
Voici la règle:
1. Orienter le pouce, l'index et le majeur de la main droite afin qu'ils soient à 90° l'un de l'autre
2. Pointer le pouce dans la direction où le conducteur se déplace
3. Pointer l'index dans la direction du flux
4. Le majeur indiquera l'extrémité (+) du conducteur
La Fig. 17-7 montre l'application de la règle.
Figure 17-7 Utilisation de la règle des trois doigts de Fleming pour déterminer la polarité de la tension induite
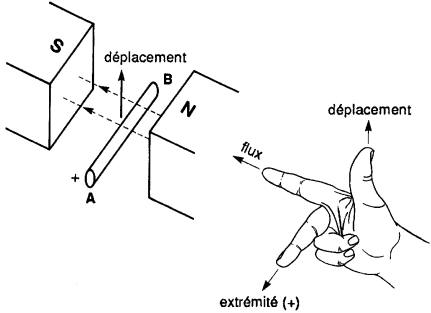
La règle de Fleming laisse parfois à désirer lorsque le flux et le déplacement du conducteur exigent une orientation inhabituelle de la main.
De plus, cette règle demande une attention spéciale dans le cas où le conducteur est stationnaire et que le flux se déplace. Pour ces raisons, nous lui préférons la règle suivante, que nous appellerons la règle du pouce:
Polarité d'une tension induite: règle du pouce
1. Étendre les doigts de la main droite de sorte que le pouce soit orienté perpendiculairement aux doigts
2. Orienter les doigts dans le sens du flux
3. Placer la paume sur le côté du conducteur qui coupe le flux
4. Le pouce indiquera l'extrémité (+) du conducteur
La Fig. 17-8 montre l'application de cette règle
Figure 17-8 Utilisation de la règle du pouce pour déterminer la polarité de la tension induite
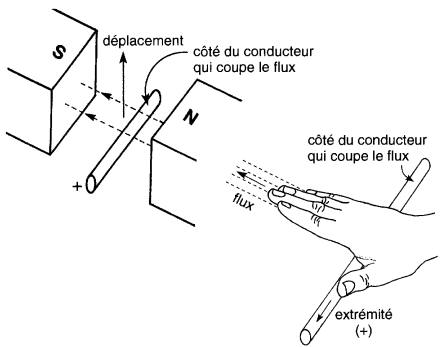
Conducteur fermé sur une résistance
Lorsque le conducteur qui coupe des lignes de flux n'est relié à aucune résistance extérieure, on n'a aucun effort à fournir pour le déplacer dans le champ magnétique.
Si, par contre, il est fermé sur une résistance (Fig. 17-9), la tension induite aux bornes du conducteur fait circuler un courant.
Figure 17-9 Le déplacement du conducteur induit une tension.
Si le conducteur est raccordé à une charge, la tension induite provoque la circulation d'un courant. À son tour, le courant, situé dans un champ, engendre une force qui s'oppose au déplacement
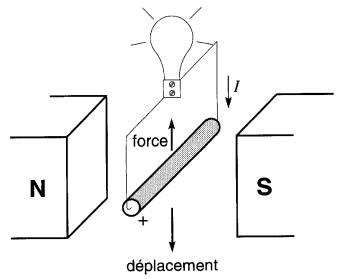
Or, nous avons vu à la section Forces électromagnétiques que le passage d'un courant dans un champ magnétique donne naissance à une force électromagnétique.
Le sens de cette force mécanique est tel qu'elle s'oppose toujours au déplacement du conducteur. Pour faire circuler un courant dans cette résistance, il faut donc vaincre la force qui s'oppose au déplacement du conducteur.
En d'autres termes, pour produire de l'énergie électrique, il faut accomplir un certain travail mécanique. Le courant est parfois appellé «courant induit». Cependant, il est important de retenir que c'est la tension qui est induite et que c'est elle qui donne naissance au courant.
Forme d'onde de la tension induite
La formule E = Blv donne la valeur instantanée de la tension induite. Pour une longueur de conducteur et une vitesse données, la valeur de la tension induite dépend de la densité de flux dans lequel le conducteur se trouve.
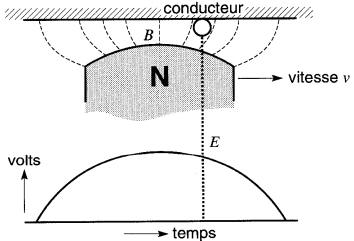
Considérons, par exemple, un conducteur stationnaire fixé dans l'entrefer d'une machine. Le conducteur coupe les lignes provenant du pôle nord d'un aimant permanent, qui se déplace vers la droite à une vitesse constante (Fig. 17-10).
Figure 17-10 La forme d'onde de la tension induite est une réplique de la densité de flux
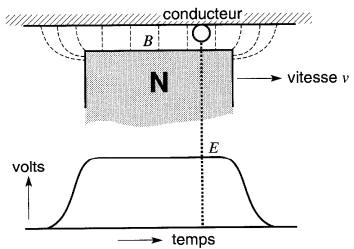
À cause de la longueur uniforme de l'entrefer, la densité Best constante partout, sauf aux extrémités du pôle N où les lignes sont moins denses.
À mesure que le pôle N se déplace, la tension instantanée prend des valeurs qui correspondent à la densité de flux à laquelle est soumis le conducteur à ce moment. La forme d'onde de la tension en fonction du temps est donc identique à la distribution du flux dans l'entrefer.
Si l'on change la forme du pôle afin de créer une densité qui diminue progressivement du centre vers les extrémités, on obtient une tension ayant une forme d'onde «arrondie» comme sur la Fig. 17-11.
Figure 17-11 En modifiant la forme d'un pôle on modifie la forme d'onde de la tension induite
On peut ainsi générer des formes d'ondes spéciales en faisant varier le spectre du champ magnétique.
Tension induite dans un cadre
À la suite de la découverte de la loi de l'induction par Faraday, les scientifiques et les techniciens du 19e siècle ne tardèrent pas à inventer et à construire toutes sortes de machines pouvant générer de l'électricité par des moyens mécaniques.
Le principe de fonctionnement de ces machines est toujours basé sur le mouvement relatif d'une bobine en forme de cadre par rapport à un champ magnétique. Considérons un aimant permanent N,S tournant autour d'un axe à l'intérieur d'un anneau de fer F fixe (Fig. 17-12).
Figure 17-12 Construction élémentaire d'un alternateur. Le flux créé par un aimant coupe les conducteurs d'une spire
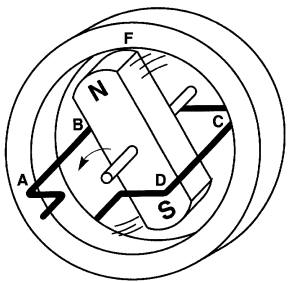
L'anneau de fer diminue la réluctance du chemin magnétique, ce qui augmente le flux dans l'entrefer. Une spire métallique en forme de cadre, ouverte à ses extrémités A et D, est fixée à l'intérieur de l'anneau, mais isolée de celui-ci.
Supposons que l'aimant tourne dans le sens antihoraire à une vitesse uniforme de 1 tour par seconde. Il est évident qu'une tension est induite dans les conducteurs AB et CD quand ils sont coupés par le flux provenant des pôles N et S.
Déterminons la valeur et la polarité de la tension induite lorsque l'aimant, en tournant, occupe successivement les positions 0°, 90°, 180° et 270°. Ces positions correspondent respectivement à l'angle en degrés dont l'aimant a tourné par rapport à sa position initiale (Fig. 17-13).
Figure 17-13 Valeur et polarité de la tension induite pour 4 positions de l'aimant tournant
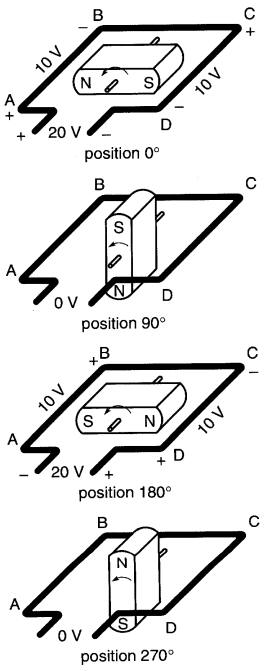
À la position 0°, le pôle N se déplace vers le bas. Si on applique la règle de la main droite ou la règle du pouce au conducteur AB, on trouve que l'extrémité A est positive par rapport à B.
De la même façon, le pôle S. se déplaçant vers le haut, induit une tension dans le conducteur CD de sorte que C soit positif par rapport à D. C'est dans cette position de l'aimant que la tension induite est la plus grande car la densité de flux coupé par les conducteurs est la plus élevée.
Supposons que cette valeur maximale de la tension induite soit de 10 volts par conducteur.
Nous aurons alors
EAB= +10V
ECD= +10V
Les conducteurs AB et CD étant en série, la tension entre les extrémités A et D du conducteur est de 20 V, A étant positif par rapport à D. EAD = +20 V.
À la position 90°, la densité de flux autour des conducteurs est nulle, donc la tension induite est nulle. EAD = 0.
À la position 180°, les conditions sont identiques à celles de la position 0° sauf que les conducteurs AB et CD sont coupés respectivement par les flux provenant du pôle S et du pôle N.
Il s'ensuit que les tensions induites seront identiques mais de polarités contraires à celles de la position 0°. EAD = -20 V.
À la position 270°, la tension induite est nulle pour la même raison qu'à la position 90°. EAD = 0.
À la position 360° (pas montrée sur la figure), l'aimant reprend sa position initiale. EAD = +20 V.
À la position 45° (pas montrée sur la figure), l'aimant fait un angle de 45° avec la position initiale.
Puisque la densité de flux autour des conducteurs a diminué par rapport à sa valeur maximale, la tension induite EAD prend une valeur intermédiaire comprise entre +20 V et 0 V disons 14 volts. EAD = + 14 V.
Nous analyserons ces résultats de plus près dans les sections qui suivent.
Courbe de la tension induite
On peut représenter sur un graphique les différentes valeurs que prend la tension induite EAD pour chacune des positions occupées par l'aimant. On obtient alors une courbe ondulée (Fig. 17-14).
Figure 17-14 Forme d'onde de la tension EAD en fonction de l'angle de rotation
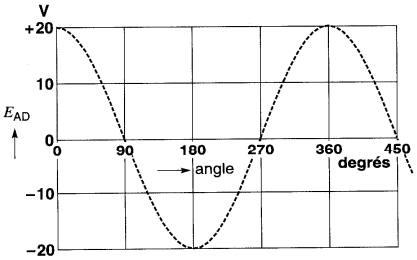
On voit sur cette courbe que, durant le premier quart de tour (0° à 90°), la tension induite est positive (A positif par rapport à D) et tombe progressivement de 20 volts jusqu'à zéro.
Pendant le deuxième quart de tour (90° à 180°), la courbe descend au-dessous de l'axe horizontal et prend des valeurs négatives (car A est devenu négatif par rapport à D).
Au troisième quart de tour. l a tension induite passe de la valeur maximale négative (-20 volts) à zéro.
Enfin, après le tour complet (à 360°), la tension induite reprend sa valeur maximale positive.
Tout comme une automobile doit ralentir puis s'arrêter avant de reculer, la valeur positive de la tension induite diminue puis s'annule avant de devenir négative.
Une tension dont la polarité alterne successivement d'une valeur positive à une valeur négative est appelée tension alternative. Les machines qui génèrent ces tensions s'appellent alternateurs ou génératrices à courant alternatif.
Courbe de la tension induite en fonction du temps
Étant donné que l'aimant est entraîné à une vitesse uniforme, chacune des positions de la Fig. 17-13 correspond à un intervalle de temps écoulé.
Puisque l'aimant tourne à une vitesse de 1 tour par seconde, le passage de l'aimant de la position 0° à la position 360° correspond à une seconde. On peut donc représenter sur la Fig. 17-15 les différentes valeurs de la tension induite correspondant au temps écoulé.
Figure 17-15 Forme d'onde de EAD en fonction du temps. Définition du cycle.
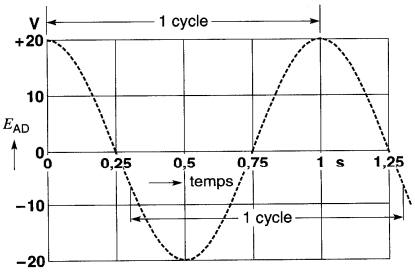
Chaque fois que l'aimant occupe une même position entre les deux pôles, la tension induite a la même valeur et la même polarité. L'aimant tournant à une vitesse uniforme, la tension induite reprend la même valeur et la même polarité à intervalles réguliers. Une grandeur qui se répète ainsi continuellement dans le temps porte le nom de grandeur périodique.
Cycle et fréquence
L'intervalle de temps mis par l'aimant pour exécuter un tour complet s'appelle cycle. On dira encore qu'un cycle est l'intervalle de temps qui sépare deux passages successifs de la tension par une même valeur et avec le même taux de variation.
À la Fig. 17-15, la durée d'un cycle de la tension alternative est de 1 seconde.
La Fig. 17-16 représente une onde de tension alternative industrielle dont la durée d'un cycle est de 1/60e de seconde.
Figure 17-16 Tension industrielle à 60 Hz ayant une valeur crête de 169,7 V. La valeur efficace de cette tension est de 120 V
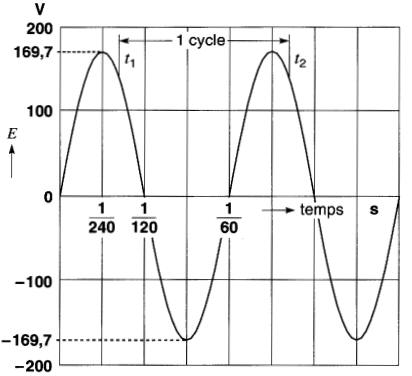
Entre les instants tt et t2, il s'écoule un cycle complet car l'onde de tension passe par les mêmes valeurs et le même taux de variation. La fréquence d'une onde périodique désigne le nombre de cycles par seconde.
Lorsqu'une tension périodique complète un cycle en 1/60e de seconde, sa fréquence est de 60 cycles par seconde, car 60 cycles sont répétés à chaque seconde.
La fréquence des tensions industrielles est imposée; elle est de 60 cycles par seconde sur presque tout le continent nord-américain et de 50 cycles par seconde dans la plupart des autres pays du monde. Gunité SI de fréquence est le hertz (Hz); il vaut un cycle par seconde. Une fréquence de 60 cycles par seconde correspond donc à une fréquence de 60 Hz.
Valeur de la tension induite
1. Effet du nombre de spires
Dans l'exemple précédent (Fig. 17-13), l'aimant tournait à une vitesse de 60 tours par minute et la bobine ne portait qu'une seule spire.
Si le nombre de spires est augmenté à 10, on constate que la tension induite EAD devient 10 fois plus grande.
Sa valeur crête (ou valeur maximale) atteindra maintenant 200 volts. En somme, la tension induite est proportionnelle au nombre de spires du cadre. Si la vitesse ne change pas, la fréquence de la tension induite restera la même, soit 1 cycle par seconde ou 1 Hz.
2. Effet de la vitesse de rotation
Si la vitesse de l'aimant est doublée, il met deux fois moins de temps à parcourir un tour complet, et la durée d'un cycle devient évidemment la moitié de ce qu'elle était, soit 0,5 seconde. La fréquence de la tension induite est donc doublée, devenant 2 Hz. De plus, en tournant deux fois plus vite, les conducteurs coupent deux fois plus de lignes en une seconde.
Par conséquent, la tension induite devient deux fois plus grande. En résumé, la fréquence et la tension induite sont proportionnelles à la vitesse de rotation.
3. Effet du flux
Si le flux créé par les pôles est doublé, la tension induite double également car le nombre de lignes coupées par seconde est doublé; la tension induite varie donc proportionnellement au flux.
4. Effet de la forme des pôles Si l'on change la forme des pôles, on peut générer des tensions ayant des formes d'ondes différentes. Si le flux total produit par chaque pôle reste fixe, la valeur moyenne de la tension induite pendant un demi-cycle demeure constante.
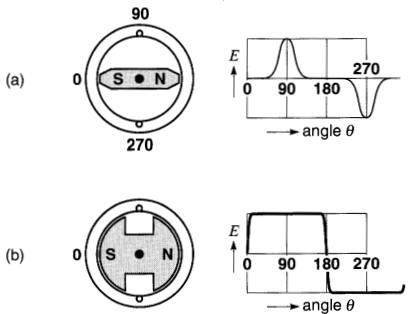
La Fig. 17-17 donne quelques exemples de formes d'ondes que l'on peut générer en faisant varier la forme des pôles.
Figure 17-17 Influence de la forme des pôles sur la forme d'onde de la tension induite.
a. pôles minces et pointus produisant une tension composée d'impullsions (+) et (-) de courte durée
b. pôles larges avec entrefer uniforme produisant une tension e forme rectangulaire
Alternateur à cadre tournant
Si l'on raccorde une charge aux bornes du cadre de la Fig. 17-12, la tension alternative induite fait circuler un courant dans la charge et dans le cadre. Puisque la polarité de cette tension varie continuellement, le courant change continuellement de sens.
Ce courant est donc un courant alternatif ayant la même fréquence que la tension qui le produit. On peut réaliser un alternateur dans lequel l'aimant permanent est fixe et le cadre tourne (Fig. 17-18a).
Figure 17-18 Alternateur élémentaire dans lequel le cadre tourne, alors que l'aimant est fixe. Cette inversion des rôles exige l'emploi de bagues et de balais.
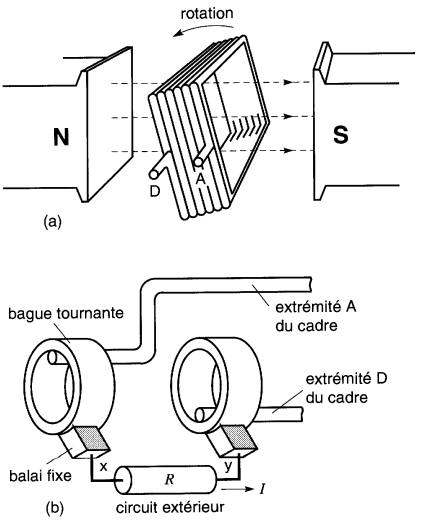
Étant donné que le mouvement relatif du cadre par rapport à l'aimant est le même que précédemment, la valeur, la polarité et la forme d'onde de la tension seront identiques.
Cependant, comme, d'une part, la tension est induite dans un cadre tournant et que, d'autre part, la charge à raccorder au cadre est stationnaire, il faut trouver un moyen pour raccorder ces éléments fixe et tournant. La seule solution consiste à employer deux balais glissant respectivement sur deux bagues (Fig. 17-18b).
Ces bagues sont soudées à chaque extrémité du cadre et tournent autour de l'axe de rotation de celui-ci. Deux balais fixes frottent sur chacune des bagues et permettent ainsi de raccorder le cadre à une charge extérieure.
Génératrice à courant continu
Si, par un dispositif quelconque, on pouvait relier un balai à l'une des extrémités du cadre tournant, et à l'autre extrémité lorsque la tension serait sur le point de changer de polarité, on obtiendrait aux bornes du cadre une tension qui aurait toujours la même polarité.
On arrive à ce résultat par l'emploi d'un collecteur (Fig. 17-19).
Figure 17-19 On peut convertir un alternateur en génératrice à courant continu par l'ajout d'un collecteur
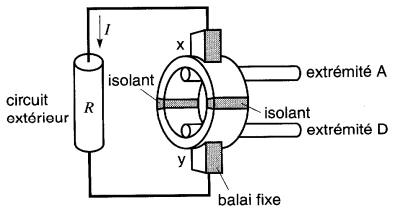
Ce collecteur, dans sa forme la plus simple, est constitué de deux demi-bagues isolées l'une de l'autre :
une lame est relié à l'extrémité A du cadre, et l'autre à l'extrémité D. Le collecteur tourne avec le cadre et la tension induite entre les lames est recueillie par deux balais fixes x et y qui frottent sur le collecteur.
Supposons encore que le cadre tourne à une vitesse uniforme de 60 tours par minute et que la tension maximale induite dans chacun des conducteurs soit de 10 volts.
La Fig. 17-20 donne les valeurs de la tension EAD induite aux bornes de la bobine, et de la tension Exy qui apparaît entre les balais, pour chacune des positions occupées successivement par le cadre.
Figure 17-20 Polarité de la tension EAD du cadre et de la tension Exy aux bornes de la charge pour 4 positions du cadre
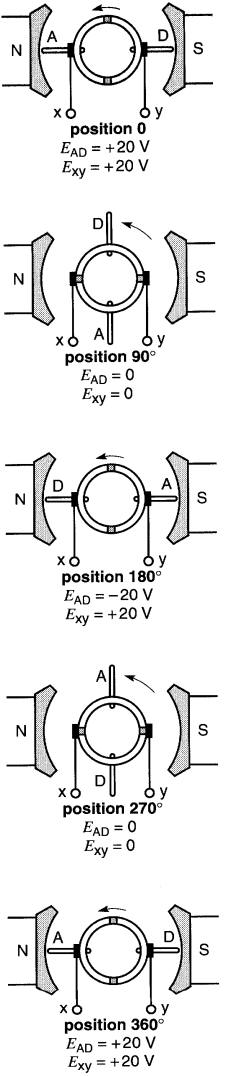
On constate que les lames (qui sont soudées aux extrémités du cadre) mangent continuellement de polarité, tandis que les balais conservent toujours la même polarité.
En effet, à la position 0°, EAD = +20 V et Exy = +20 V. Quand le premier quart de tour est terminé (position 90°), la tension induite est nulle, et l'inversion des contacts est en train de s'effectuer.
Pendant le deuxième quart de tour, le balai x, qui frottait précédemment sur la lame A, est maintenant en contact avec la lame D. L'inverse s'est produit pour le balai y. Bien que la polarité de chacune des lames ait changé, celle des balais est restée la même.
À la position 180° on a:
EAD = -20V et Exy = +20 V
la fin du troisième quart de tour (position 270°), la tension s'annule de nouveau.
Ensuite, durant le quatrième quart de tour, le contact des balais sur les lames s'inverse et, à la position 360°, l'on revient à la position 0°, donc aux mêmes valeurs et aux mêmes polarités.
La tension entre les balais x et y a varié entre 0 et 20 volts mais n'a pas changé de polarité. On dit qu'elle a été redressée. La représentation graphique de la tension Exy est donnée à la Fig. 17-21.
Figure 17-21 Forme d'onde de la tension aux bornes de la charge
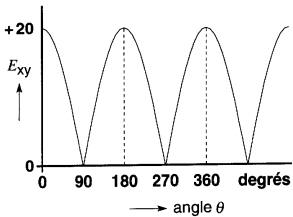
La tension obtenue n'est pas parfaitement continue, comme celle fournie par une batterie, mais elle oscille entre une valeur maximale et une valeur nulle; une telle onde est dite pulsative.
Le lecteur a probablement réalisé que le collecteur agit simplement comme un commutateur mécanique qui intervertit les bornes du cadre dès que la polarité de la tension est sur le point de changer.
Puisque la tension entre les balais a toujours la même polarité, le courant circulant dans une charge extérieure aura toujours le même sens.
Par conséquent, la machine représentée à la Fig. 17-19 porte le nom de génératrice à courant continu, ou dynamo.
Amélioration de la forme d'onde
On réussit à améliorer la forme d'onde de la tension continue en utilisant quatre cadres et quatre lames disposés en angle droit (Fig. 17-22).
Figure 17-22 Génératrice à 4 bobines avec un collecteur à 4 lames
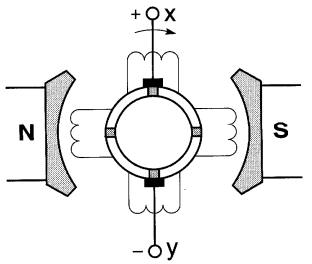
La forme d'onde de la tension obtenue est donnée à la Fig. 17-23. On voit que la tension varie encore quelque peu mais ne tombe jamais à zéro ; elle se rapproche davantage d'une tension parfaitement continue.
En multipliant les bobines et les lames, on obtient une tension induite à peu près invariable. Dans les dynamos modernes, l'ondulation de la tension est inférieure à 5 % de sa valeur moyenne.
Différence entre un alternateur et une dynamo
Les alternateurs et les dynamos étudiés aux sections précédentes ont une construction à peu près identique : dans les deux cas un cadre tourne entre les pôles d'un aimant. Ils se différencient seulement par la façon dont le cadre est relié aux balais: les alternateurs portent des bagues alors que les dynamos exigent un collecteur composé de lames (Fig. 17-24).
Figure 17-24 Construction fondamentale de trois types de génératrices:
a. La dynamo utilise un
collecteur;
b. L'alternateur utilise des bagues;
c. Une
dynamo/alternateur utilise un collecteur et des bagues
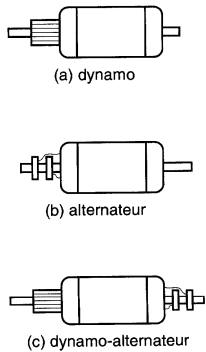
On réalise des machines (Fig. 17-24c) qui portent à la fois des bagues et des lames, et qui peuvent fonctionner simultanément comme alternateur et comme dynamo.
Toutefois, les alternateurs de grande puissance qui génèrent l'électricité qu'on utilise sont tous construits avec des électro-aimants tournants et des cadres (ou enroulements) fixes. La construction de ces machines sera étudiée à la section Alternateurs triphasés.
Résumé
Cette section nous a permis de découvrir un des phénomènes les plus importants de l'électrotechnique : la loi de l'induction électromagnétique de Faraday.
Selon ce principe une tension est induite dans un conducteur en mouvement dans un champ magnétique, ou plus généralement, lorsque le conducteur « coupe » les lignes de force d'un champ. Cette tension dépend seulement du taux de changement Δθ/Δt du flux balayé par le conducteur. Nous avons vu qu'une formule pratique permet de calculer la tension induite dans un conducteur rectiligne.
Nous avons aussi appris deux règles simples permettant de trouver la polarité de la tension induite. La loi de l'induction de Faraday est à l'origine des machines tournantes générant de l'électricité : génératrices à courant continu et alternateurs générant une tension alternative.
Dans ces machines une tension est induite dans les conducteurs balayés par un champ magnétique créé par un électro-aimant ou par un aimant permanent.
Dans les alternateurs, une tension alternativement positive et négative se répète à chaque cycle. Le nombre de cycles par seconde correspond à la fréquence exprimée en hertz (Hz). Dans les machines à courant continu, on utilise un commutateur mécanique, le collecteur, pour redresser la tension et obtenir une tension continue.
PROBLÈMES
Niveau pratique
17-1 Quelle quantité de flux faut-il couper par seconde pour induire une tension de 1 volt dans un conducteur?
17-2 Lorsqu'un conducteur ouvert coupe des lignes de flux, un courant est-il induit?
17-3 Énoncer la règle donnant la polarité de la tension induite dans un conducteur.
17-4 Tracer la forme d'onde de la tension induite dans un alternateur.
17-5 Qu'entend-on par cycle? par fréquence?
17-6 Quel est l'effet du nombre de spires d'une génératrice sur la valeur de la tension induite? Quel est l'effet de la vitesse de rotation?
17-7 Qu'est-ce qui différencie une dynamo d'un alternateur?
17-8 À quoi sert le collecteur d'une dynamo?
17-9 En traversant un champ magnétique, un conducteur coupe un flux de 3 Wb en 0,1 s. Quelle est la tension induite? La valeur de cette tension dépend-elle de la forme du conducteur?
17-10 En utilisant la règle des trois doigts et la règle du pouce, vérifier la polarité des tensions induites dans les Fig. 17-1, 17-3, 17-5, 17-6, 17-9 et 17-13.
Niveau intermédiaire
17-11 Un conducteur de 2 m de longueur se déplace à une vitesse de 60 km/h dans un entrefer où règne une densité de 0,6 T. Calculer la tension induite dans ce conducteur.
17-12 Dessiner schématiquement un alternateur simple.
17-13 Un alternateur bipolaire tourne à une vitesse de 1200 r/min. Quelle est la fréquence de la tension induite? quelle est la durée d'un cycle?
17-14 Un alternateur bipolaire doit produire une tension de fréquence 60 Hz. Quelle doit-être sa vitesse de rotation?
17-15 Une tension de 240 V et de fréquence 50 Hz est induite dans un alternateur. Quelle sera la nouvelle tension induite
si : a) le nombre de spires de l'induit est doublé b) la vitesse de rotation est réduite de moitié c) le flux est doublé
17-16 Quelle est la polarité de la borne A de la Fig. 17-4?
17-17 Dans la Fig. 17-10, quelle est la polarité de l'extrémité du conducteur dirigée vers le lecteur?
Niveau avancé
17-18 Les alternateurs de 500 MVA installés à Churchill Falls ont les caractéristiques suivantes :
diamètre du rotor: 9,19 m
vitesse de rotation: 200 r/min
densité de flux au centre d'un pôle: 1,5 T
longueur des conducteurs: 2,9 m
Calculer la valeur de la tension crête induite dans les conducteurs.
Réponses
1) 1 Wb; 9) 30 V; non; 11) 20
V; 13) 20 Hz; 50 ms;
14) 3600 r/min; 15a) 480 V; 15b) 120 V; 15c) 480 V; 16)
négative;
17) négative; 18) 419 V
