Solutions des circuits à courant alternatif
Il est indispensable de connaître quelques principes de base sur la résolution des circuits à c.a. Ces règles sont faciles à utiliser et elles nous aideront à comprendre le fonctionnement des moteurs, génératrices, lignes de transport et, plus généralement, de tout dispositif fonctionnant à courant alternatif.
Dans cette section, nous utiliserons trois méthodes pour résoudre les circuits parallèles, séries et mixtes :
méthode:
1 : résolution par diagrammes vectoriels tracés à l'échelle. Cette méthode graphique ne nécessite que des calculs simples et permet de visualiser les tensions et les courants.
2: résolution à l'aide de formules mathématiques. Ces formules permettent de résoudre les circuits plus rapidement mais elles sont limitées aux circuits simples.
3: résolution par les techniques de calcul vectoriel présentées à la section Diagrammes vectoriels.
Cette méthode est la plus générale. Elle est plus précise que la méthode graphique et permet de résoudre des circuits complexes. Il existe en effet plusieurs méthodes permettant de résoudre les circuits à c.a., chacune ayant une utilité particulière.
Ainsi, les équations différentielles et les transformées de Laplace servent à analyser les phénomènes transitoires, tandis que le calcul vectoriel utilisant les nombres complexes convient pour résoudre les circuits en régime permanent, lorsque les tensions et les courants sont sinusoïdaux.
Cependant, la méthode graphique (méthode 1), appuyée au besoin par une connaissance de la trigonométrie, suffit pour résoudre la majorité des problèmes quotidiens.
Impédance d'un circuit
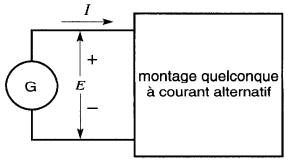
Le rapport E/I dans un circuit à courant alternatif s'appelle l'impédance du circuit (Fig. 24-1) et il se mesure en ohms.
Figure 24-1 Définition de l'impédance et de la puissance apparente d'un circuit à courant alternatif
L'impédance (symbole Z) représente la «résistance» que le circuit offre au passage d'un courant alternatif. Par exemple, si la tension efficace aux bornes d'un montage quelconque est de 120 V et le courant de 4A, l'impédance du circuit est :
Z = E/I = 120V/4A = 30Ω
Le terme «impédance» englobe toutes les sortes d'opposition d'un circuit au passage d'un courant alternatif y compris la résistance d'un élément chauffant, la réactance inductive d'une bobine, la réactance capacitive d'un condensateur et toute combinaison imaginable de ces trois composants fondamentaux.
Puissance apparente
La puissance apparente S d'un circuit à courant alternatif est égale au produit de la tension efficace E à ses bornes par le courant efficace I qui circule (Fig. 24-1).
La puissance apparente se mesure en volts-ampères (VA) ; on utilise souvent les multiples de cette unité, soit le kilovolt-ampère (kVA) et le méga voltampère MVA).
La Fig. 24-1 peut représenter un montage complexe contenant des éléments résistifs, inductifs et capacitifs. Le montage peut aussi comprendre des sources de tension. La puissance apparente englobe donc toutes les formes de puissances, à savoir les puissances actives (watts), les puissances réactives (vars) et toute combinaison possible de ces deux puissances. Cela nous permet d'écrire les formules générales suivantes :
Z = E / I (24-1)
S = E / I (24-2)
où
Z = impédance du circuit, en
ohms [Ω]
S = puissance apparente, en volts-ampères [VA]
E = tension
sinusoïdale efficace, en volts [V]
I = courant sinusoïdal efficace, en
ampères [A]
SOLUTION DES CIRCUITS PAR LA MÉTHODE GRAPHIQUE (Méthode 1)
Les exemples numériques suivants indiquent comment résoudre les circuits parallèle, série et mixte. Les vecteurs y sont tracés à l'échelle, ce qui permet de mesurer leurs amplitudes avec une règle, et leurs angles de phase avec un rapporteur.
Solution graphique d'un circuit parallèle
L'exemple numérique suivant indique comment résoudre un circuit parallèle.
Exemple 24-1
Le circuit de la Fig. 24-2a comprend une résistance de 30Ω et une réactance capacitive de 16Ω raccordées en parallèle sur une source de 240 V.
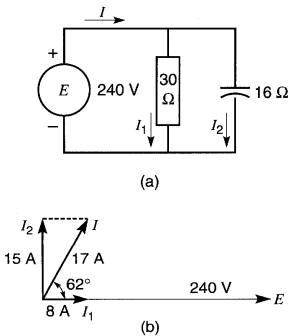
Figure 24-2
a. Circuit parallèle
b. Résolution du circuit (voir exemple 24-1)
Trouver:
a) le courant I et son déphasage par rapport à la tension E
b) l'impédance du circuit
c) les puissances active. réactive et apparente du circuit
Solution
a) Pour trouver la valeur du courant I, on doit d'abord calculer la valeur de I1 dans la résistance de même que 12 dans la réactance capacitive, et ensuite tracer un diagramme vectoriel.
1. La tension étant commune aux deux éléments, on la choisit comme vecteur de référence. Traçons le vecteur dans le sens horizontal.
2. I1 = 240 V/30Ω = 8A. L'élément de 30Ω étant résistif, le courant I1 est en phase avec la tension.
3. 12 = 240 V/16Ω = 15A. L'élément de 16Ω étant capacitif, ce courant est déphasé de 90° en avance sur la tension.
4. Le courant I est égal à la somme vectorielle
I=I1+I2
D'après le diagramme vectoriel, tracé à l'échelle (Fig. 24-2b), on trouve que I possède une valeur de 17A efficace. Un rapporteur indique qu'il est déphasé de 62° en avant de la tension.
b) L'impédance du circuit est:
Z= E/ I= 240V / 17A = 14,1Ω
Noter que l'impédance est une propriété d'un circuit et qu'elle est indépendante de la valeur de la tension appliquée. Cependant, l'impédance dépend de la fréquence de la source, car la valeur des réactances inductives et capacitives varie avec la fréquence.
c) L'élément résistif de 30Ω consomme une puissance active:
P= EI1 =240V x 8A = 1920W
L'élément capacitif de 60 S2 représente une puissance réactive:
Q = EI2 = 240V x 15A = 3600var
La puissance apparente du circuit est:
S = EI = 240 x 17 =4080 VA
On observe que la puissance apparente n'est pas égale à la somme arithmétique des puissances active et réactive:
4080 1920 + 3600.
Solution graphique d'un circuit série
L'exemple numérique suivant indique comment résoudre un circuit série.
Exemple 24-2
Soit un circuit (Fig. 24-3) formé d'une résistance de 12Ω en série avec une réactance inductive de 5Ω, et parcouru par un courant I de 10A.
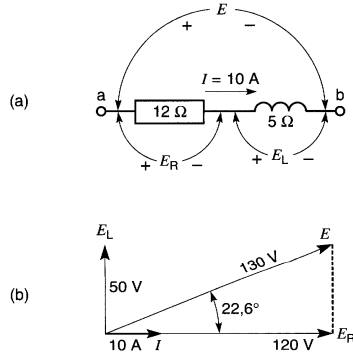
Figure 24-3 a. Circuit série; b. Résolution du circuit (voir exemple 24-2).
Trouver:
a) la tension E et son déphasage par rapport au courant I
b) l'impédance du circuit
c) les puissances active, réactive et apparente du circuit Solution
a) Puisque le courant I est le même pour les deux éléments considérés, prenons-le comme vecteur de référence.
On le trace horizontalement vers la droite. La tension aux bornes de la résistance est :
ER = 10A x 12Ω = 120V
Puisque le courant dans une résistance est en phase avec la tension, nous traçons sur le diagramme un vecteur ER dans la même direction que le vecteur I; la longueur de ce vecteur, mesurée à l'échelle, correspond à 120V Le courant de 10A traversant une réactance inductive de 5Ω produit une tension EL de:
EL =10A x 5Ω = 50V
Puisque, dans une inductance, le courant I doit être déphasé de 90° en arrière de la tension, il faut tracer le vecteur EL dans une direction perpendiculaire à celle du vecteur I et de façon à ce que EL soit décalé de 90° en avant de I (Fig. 24-3b). La tension totale E aux bornes du circuit est donnée par la somme vectorielle de ER et EL.
En la mesurant à l'échelle, on trouve E= 130V.
De plus, un rapporteur indique que E est en avance sur I de 22,6°.
Noter que la tension totale aux bornes du circuit n'est pas égale à (120 + 50) = 170 V, car les tensions ER et EL ne sont pas en phase.
b) L'impédance du circuit est Z = E/I = 130V/10A = 13Ω
c) La puissance apparente du circuit est:
S = EI = 130V x 10 A= 1300 VA
La puissance active est
P = ERI = 120V x 10A = 1200W
La puissance réactive est:
Q= ELI = 50V x 10A = +500 var
Solution graphique d'un circuit mixte
La solution générale des circuits mixtes (série-parallèle) exige l'utilisation du calcul vectoriel. On peut, cependant, utiliser une méthode graphique dans plusieurs cas.
En voici un exemple.
Exemple 24-3
Déterminer l'impédance entre les points a et h du circuit mixte de la Fig. 24-4.
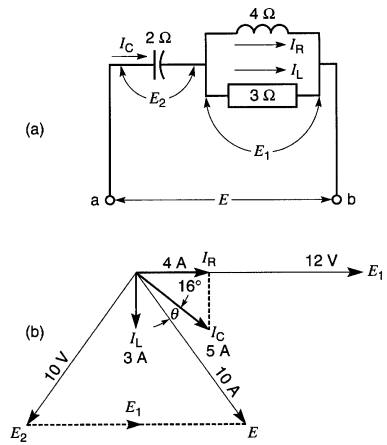
Figure 24-4 a Circuit mixte; b) Résolution du circuit mixte (voir exemple 24-3)
Solution
Puisque l'mpétance d'un circuit n'est pas affectée par la tension qu'on lui applique, supposons que la tenon E1 soit de 12 V et choisissons cette tension comme secteur de référence. On le trace horizontalement vers la droite.
Un courant IR a donc une valeur de :
IR = 12V / 3Ω = 4A
et son vecteur est en phase avec E1.
Le courant IL a une valeur de:
IL = 12V / 4Ω = 3A
et son vecteur est 90° en arrière de E1. Le courant le dans le condensateur est égal à la somme vectorielle de IR et de IL et sa valeur (mesurée à l'échelle) est de 5A.
La tension E2 aux bornes du condensateur est donc :
E2 = IcXc = 5A x 2Ω = 10V
Le vecteur E2 doit être tracé 90° en arrière de le car le courant dans un condensateur est toujours 90° en avant de la tension. La tension E (entre les bornes a et b) est donnée par la somme vectorielle de E1 et de E2, ce qui donne 10V (mesurée à l'échelle).
L'impédance Zab du circuit est donc:
Zab = E / Ic = 10V / 5A = 2Ω
À l'aide d'un rapporteur, on trouve que le courant le est déphasé de 16° en avant de la tension E.
SOLUTION DES CIRCUITS SIMPLES À L'AIDE DE FORMULES (Méthode 2)
Formules donnant l'impédance de deux éléments en série
On a souvent besoin de calculer l'impédance d'un circuit composé de deux éléments en série. Lorsque les éléments sont de même nature, on additionne simplement leurs impédances, mais quand ils sont différents on est obligé d'utiliser des méthodes vectorielles pour obtenir l'impédance totale.
Il est alors très utile d'avoir recours à une formule permettant de calculer l'impédance directement. Il existe trois possibilités de raccordement de deux éléments différents en série (Fig. 24-5, 24-6 et 24-7).
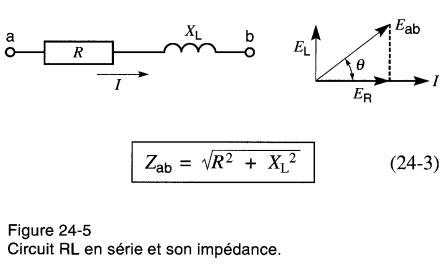
Considérons le circuit de la Fig. 24-5 : il comprend une résistance R et une réactance inductive XL. Nous démontrons ci-après que la valeur de l'impédance Zab entre les bornes a et b est donnée par la formule 24-3, soit
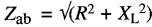
Supposons qu'un courant de I ampères traverse ce circuit. Il produit une tension ER aux bornes de la résistance et une tension EL aux bornes de l'inductance.
Les vecteurs de ces deux tensions sont tracés à partir du vecteur du courant I qui constitue le vecteur de référence (voir le diagramme vectoriel de la Fig. 24-5).
La valeur Eab de la somme vectorielle de ER et de EL est évidemment égale à:
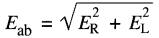
Mais
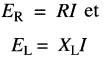
donc
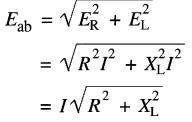
Par définition, l'impédance d'un circuit est le rapport entre la tension à ses bornes et le courant qui le parcourt; donc
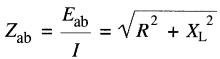
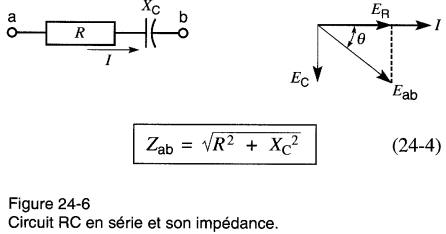
On procède de la même façon pour résoudre les circuits des Fig. 24-6 et 24-7.
On découvre alors les expressions suivantes:
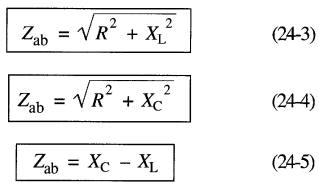
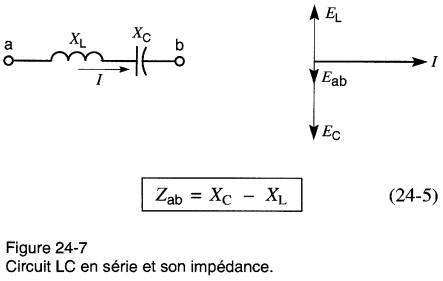
Le troisième circuit, composé de XL et Xc, demande peut-être une explication supplémentaire. Les vecteurs de tension sont tracés avec Ec (tension sur le condensateur) plus grande que EL, ce qui implique que Xc est plus élevée que XL.
Toutefois, il aurait pu arriver que XL excède Xc et, dans ce cas, le vecteur Eab aurait été en avant de I au lieu d'être en arrière, comme indiqué sur la figure. L'impédance du circuit aurait donc été égale à (XL - Xc) ohms au lieu de (Xc - XL) ohms.
Exemple 24-4
Soit le circuit de la fig. 24-8.
Figure 24-8
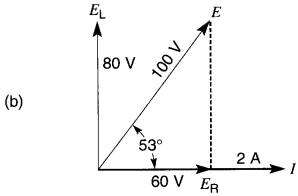
a. Circuit série (voir exemple 24-4); b. Résolution du circuit
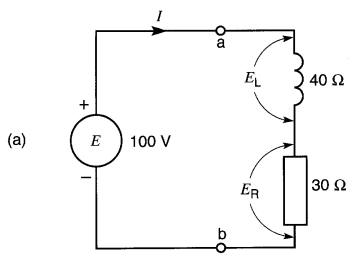
Trouver :
a) le courant I
b) les tensions ER et EL
c) la puissance apparente et la puissance active
d) le déphasage entre le courant I et la tension de la source
Solution
Trouvons d'abord l'impédance du circuit entre les bornes a et b.
D'après la formule 24-3 :
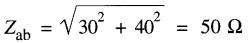
a) Courant I = E / Z = 100V / 50Ω = 2A
b) Tension EL = XLI = 40Ω x 2A = 80V
Tension ER = RI= 30Ω x 2A = 60V
c) Puissance apparente EI = 100V x 2A = 200 VA
Puissance active ERI = 60V X 2A = 120 W
d) En traçant le diagramme vectoriel (Fig. 24-8b), on trouve, avec un rapporteur, que le courant I est déphasé de 53° en arrière de la tension E.
Formules donnant l'impédance de deux éléments en parallèle
L'impédance équivalente à deux impédances Z1 et Z2 en parallèle (Fig. 24-9) est donnée par la formule suivante:
Figure 24-9 Impédances en parallèle
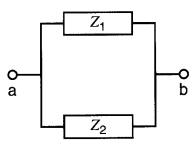
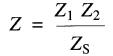(24-6)
où
Z = impédance
parallèle, en ohms [Ω]
Z1 = impédance de Z1 , en ohms [Ω]
Z2 = impédance de Z2 , en ohms [Ω]
Zs = impédance du circuit composé de Z1 et Z2 en série, en ohms [Ω]
Cette formule reste valable même si les impédances Z1 et Z2 sont constituées de groupements mixtes.
Elle nous permet d'établir l'impédance des circuits parallèles des Fig. 24-10, 24-11 et 24-12.
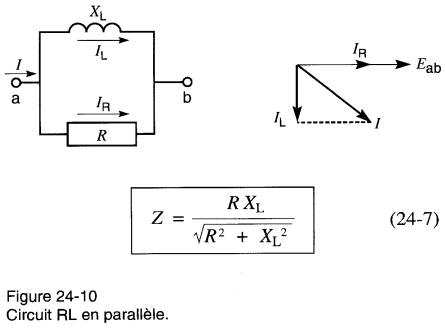
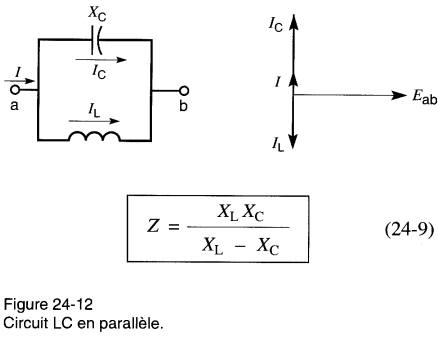
Ainsi, pour la Fig. 24-10:
ZL =XL Z2 =R
et l'impédance de Zi et Z2 en serte est donnée par l'équation 24-3.
Donc
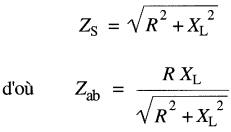
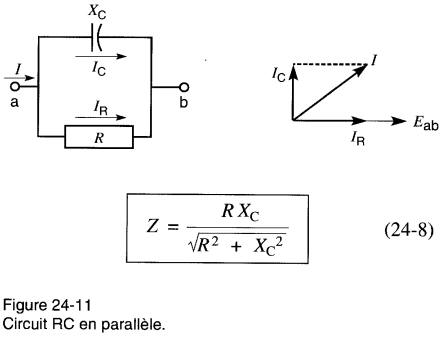
On procède de la même manière pour déterminer l'impédance des circuits des Fig. 24-11 et 24-12. On obtient alors les expressions suivantes :
Exemple 24-5
Calculer l'impédance du circuit montré à la Fig. 24-13.
Figure 24-13 Voir exemple 24-5
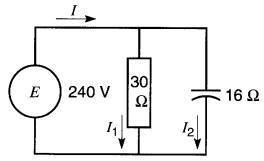
Solution Ce circuit est semblable à celui de la Fig. 24-11.
L'impédance est donc:
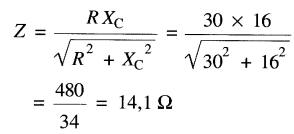
ce qui correspond exactement à la valeur que nous avons trouvée graphiquement à la section plus haut.
Circuits résonnants, fréquence de résonance
Lorsqu'un circuit est composé de plus de deux éléments, il est impossible de donner des formules universelles permettant le calcul de l'impédance du circuit.
Cependant, il existe deux circuits à trois éléments qui méritent notre attention. Il s'agit des circuits résonnants utilisés dans les filtres (Fig. 24-14 et 24-15).
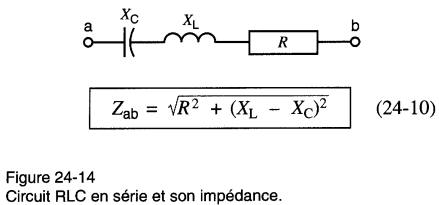
La Fig. 24-14 montre trois éléments R, XL et XC connectés en série.
L'impédance entre les bornes a et b est donnée par la formule:
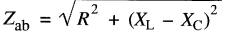(24-10)
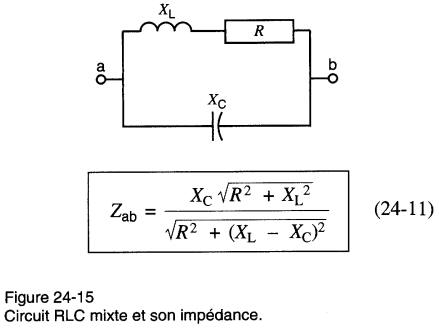
La Fig. 24-15 montre trois éléments semblables connectés en série-parallèle.
L'impédance est donnée par la formule:
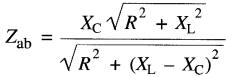(24-11)
Dans ces deux circuits, les éléments R et XL sont habituellement associés à une bobine.
Examinons maintenant le phénomène de résonance.
Dans la Fig. 24-14, le circuit est dit en résonance série lorsque XL = XC.
De la même façon, le circuit de la Fie. 24-15 est dit en résonance parallèle lorsque XL = XC.
Sachant que XL = 2πfL et que XC = 1 /2πfC, il s'ensuit que la fréquence de résonance est donnée par la formule:
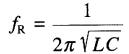(24-12)
où
fR = fréquence de résonance, en hertz [Hz]
L = inductance de la bobine, en henrys [H]
C = capacitance, en farads [F]
Circuits résonnants série et parallèle
D'après la formule 24-10,l'impédance d'un circuit résonant série est simplement égale à la résistance R. Le courant circulant dans le montage est donc I = Eab/R (Fig. 24-14).
Comme la réactance XL d'une bobine est habituellement entre 10 et 100 fois plus grande que la valeur de sa résistance R, il s'ensuit que la tension aux bornes de la bobine (composée de R en série avec XL) sera entre 10 et 100 fois la tension appliquée entre les bornes a, b du circuit.
À toutes fins utiles, la tension aux bornes du condensateur sera aussi de 10 et 100 fois la tension de la source. Ce phénomène d'amplification est illustré par l'exemple suivant.
Exemple 24-6
Un circuit résonnant série (Fig. 24-16a) comprend une bobine avant une résistance de 10 £2 et une réactance XL de 100Ω, raccordée en série avec un condensateur de réactance XC = 100Ω.
Déterminer la valeur de la tension aux bornes de chaque élément si la tension de la source est de 120V.
Solution
L'impédance du circuit est:
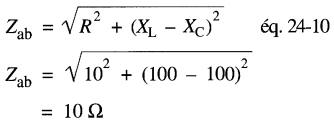
Le courant I = E/Z = 120/10 = 12 A.
Puisque l'impédance est résistive, le courant est en phase avec la tension.
Tension Ec aux bornes du condensateur :
Ec = 100S2 x 12A = 1200V, 90° en arrière de I.
Tension EL aux bornes de l'inductance :
EL= 100Ω x 12A = 1200V, 90° en avant de 1.
Tension aux bornes de la résistance: ER= 10 x 12 = 120V, en phase avec le I.
La tension EB aux
bornes de la bobine est égale à la somme vectorielle EL
+ ER.
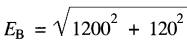
= 1206 V, 84° en avant du courant.
Noter que les tensions Ec et EB sont 10 fois plus grandes que celle de la source.
Le diagramme vectoriel est donné à la Fig. 24-16b.
Figure 24-16
a. Circuit résonnant série ;
b. Résolution du circuit (voir exemple 24-6).
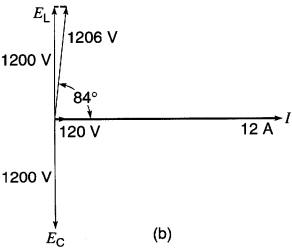
Signalons que l'on ne peut pas mesurer la valeur de EL ni celle de ER car l'inductance et la résistance de la bobine sont physiquement indissociables. Étant donné qu'on a accès seulement aux bornes de la bobine, on peut seulement mesurer la valeur de EB.
En ce qui concerne le circuit parallèle de la Fig. 24-15, son impédance lors de la résonance est obtenue en utilisant la formule 24-11.
En pratique, cette formule peut s'écrire sous une forme simplifiée.
On note en effet que l'on peut remplacer le terme i(R2 + XL2) par XL, pour autant que XL > 5R. Cette approximation introduit une petite erreur qui est inférieure à 2%.
De plus, il est évident qu'on peut remplacer Xc par XL.
On peut donc écrire:
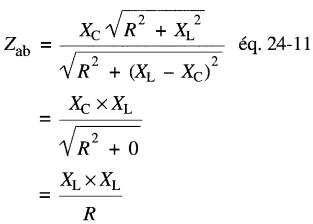
Soit:
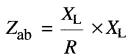(24-11a)
Étant donné que le rapport XL/R est généralement entre 10 et 100, l'impédance entre les bornes a, b est de 10 à 100 fois la valeur de XL (ou de Xc).
Donc, le courant circulant dans la bobine et dans le condensateur est de 10 à 100 fois celui fourni par la source. Cette amplification du courant peut avoir des conséquences importantes dans certains montages. Nous aurons l'occasion de le constater dans les sections qui suivent.
L' amplification de courant se produit même lorsque la résonance n'est pas parfaite. L'exemple suivant démontre l'effet d'une résonance partielle dans un montage parallèle.
Exemple 24-7
Un circuit composé d'une bobine en parallèle avec un condensateur ayant une réactance Xc de 8Ω est raccordé à une source de 200V (Fig. 24-17).
Figure 24-17 Bobine en parallèle avec un condensateur (voir exemple 24-7)
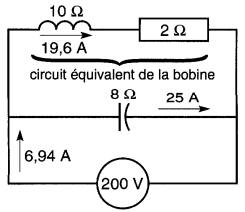
La bobine possède une résistance de 2Ω et une réactance XL
Calculer:
a) l'impédance du circuit
b) la valeur des trois courants
Solution
a) L'impédance du circuit est donnée par la formule (24-11):
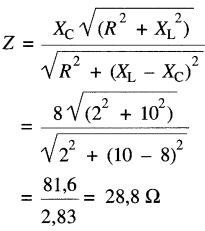
b) Le courant fourni par la source est:
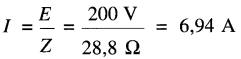
Le courant dans la bobine est:
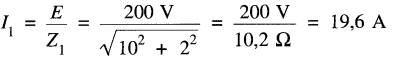
Le courant dans le condensateur est:
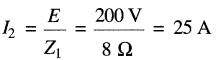
On note que le courant fourni par la source (6,94 A) est bien inférieur aux courants circulant dans le condensateur et dans la bobine. La Fig. 24-18 montre une application importante de la résonance série et parallèle.
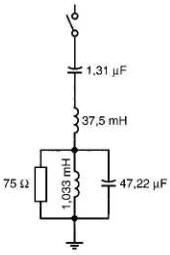
Figure 24-18 Circuit résonnant série-parallèle installé dans le réseau Hydro-Québec au poste Radisson dans le complexe de La Baie-James.
Les deux inductances situées du côté gauche, superposées l'une sur l'autre, et les condensateurs supportés par la structure du côté droit, constituent un filtre.
Celui-ci produit simultanément un circuit résonnant série pour les harmoniques de 660 Hz et de 780 Hz, sur le réseau à 60 Hz. Lorsque l'interrupteur est fermé, le filtre est soumis à une tension de 180 kV à 60 Hz (gracieuseté Hydro-Québec)
SOLUTION DES CIRCUITS PAR LE CALCUL VECTORIEL (Méthode 3)
Les méthodes graphiques que nous venons de présenter donnent la solution d'un grand nombre de circuits, mais il est souvent plus facile d'utiliser le calcul vectoriel.
Dans les paragraphes qui suivent nous donnons les éléments de base de cette troisième méthode. Cependant, nous recommandons au lecteur de réviser d'abord la section Solutions des circuits à courant continu sur les circuits à courant continu, et la section Diagrammes vectoriels.
Représentation vectorielle des éléments R, XL, Xc
On se souvient que les résistances et réactances peuvent être exprimées sous forme vectorielle:
1 Une résistance est un vecteur horizontal dirigé vers la droite. Son amplitude est égale à la valeur ohmique de la résistance.
Sa forme rectangulaire est R Sa
forme polaire est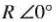 
.
2. Une réactance inductive XL est un vecteur vertical dirigé vers le haut. Son amplitude est égale à la valeur de la réactance inductive.
Sa forme rectangulaire est jXL
Sa forme polaire est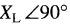 
.
3. Une réactance capacitive est un vecteur dirigé vers le bas.
Sa forme rectangulaire est jXc
Sa forme polaire est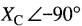 
.
Relation entre tension, courant et impédance
Avant d'entreprendre la résolution des circuits par la méthode vectorielle, il est important de se rappeler les conventions de signes associées au courant et à la tension aux bornes d'un élément.
Ces conventions sont basées sur les deux lois de Kirchhoff. La Fig. 24-19 montre un courant I circulant de gauche à droite dans une impédance Z. Il se produit donc une chute de tension entre les bornes a et b. On désire connaître la valeur de la tension Eab en fonction de I et de Z.
Figure 24-19 Relation entre E, I et Z; Eab = ZI
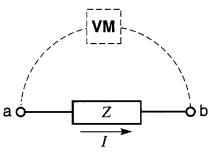
Un voltmètre VM branché aux bornes de l'impédance Z mesure la tension Eab. Appliquons la première loi de Kirchhoff à la boucle formée par le voltmètre et l'impédance Z.
En parcourant la boucle dans le sens horaire, on peut écrire:
Eab- ZI =0
soit
Eab = ZI (24-12)
Par contre, si le courant circulait de droite à gauche dans l'impédance, on obtiendrait:
Eab + ZI =0
soit
Eab = -ZI
Notons aussi qu'en tout temps, on peut écrire :
Eab = -Eba (24-13)
En résumé, le signe à utiliser dépend du sens arbitraire choisi pour le courant.
On écrira:
Eab = +ZI
si le courant dans l'impédance Z est orienté de a vers b
ou
Eab = -ZI
si le courant dans l'impédance Z est orienté de b vers a
Signalons aussi que lorsqu'un vecteur écrit sous la forme polaire est précédé d'un signe (-) on peut le ramener à une forme positive en ajoutant ou en retranchant 180° à son angle.
Par exemple, si
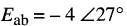
on peut écrire:
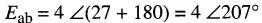
ou encore:
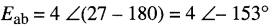
Exemple 24-8
Un courant
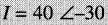
circule dans l'impédance Z = 16 + j63 (Fig. 24-20).
Déterminer la valeur et l'angle de phase de la tension E12.
Figure 24-20 Voir exemple 24-8
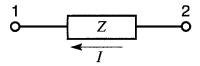
Solution
Avec le sens choisi pour le courant, on a :
Impédances des circuits série, parallèle et mixte
Les règles à utiliser pour les
groupements d'impédances en série, en parallèle ou mixtes sont les mêmes que
pour les résistances.
En voici 3 exemples.
1. Circuit série.
Soit un circuit série composé des éléments R, XL, Xc (Fig. 24-21).
Figure 24-21 Calcul de l'impédance d'un circuit série
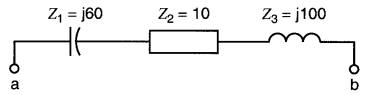
L'impédance est:
2. Circuit parallèle.
Soit le circuit parallèle de la Fig. 24-22.
Figure 24-22 Calcul de l'impédance d'un circuit parallèle
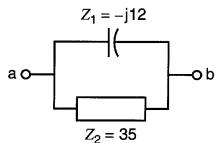
L'impédance est:
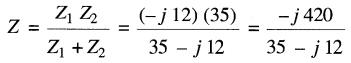
Afin de permettre la division de cette expression, nous transformons le numérateur et le dénominateur sous forme polaire:
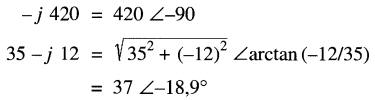
On a donc
Le circuit de la Fig. 24-22 est donc équivalent à un circuit composé d'une résistance de 3,7Ω en série avec un condensateur de réactance Xc = 10,7Ω.
3. Circuit mixte.
Soit le circuit mixte de la Fig. 24-23 (identique à celui de la Fig. 24-4).
Figure 24-23 Calcul de l'impédance d'un circuit mixte
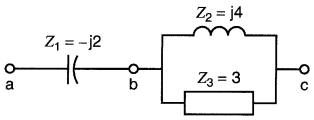
Son impédance est donnée par l'expression:
Le circuit mixte est donc équivalent à une résistance de 1,92Ω en série avec un condensateur de réactance Xc = 0,56Ω.
Résolution de circuits quelconques
À la section Solutions des circuits à courant continu nous avons présenté les deux lois de Kirchhoff et nous avons donné les règles de base permettant de résoudre n'importe quel circuit à courant continu.
Il est remarquable que les mêmes lois et les mêmes règles (y compris le théorème de Thévenin) puissent être utilisées pour résoudre les circuits à courant alternatif. Il suffit d'employer les grandeurs vectorielles pour les tensions, les courants, et les impédances.
Les exemples numériques qui suivent montrent la façon de les appliquer.
Exemple 24-9
Le circuit de la Fig. 24-24a comprend deux sources dont les tensions respectives sont:
Figure 24-24a Voir exemple 24-9
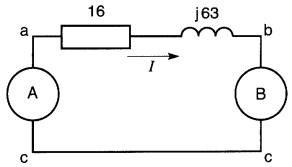
Calculer:
a) la valeur du courant I dans le circuit
b) l'angle entre I et Eac
c) la valeur de Eab et son angle de phase
Solution
a) Pour résoudre ce circuit, on doit d'abord choisir une direction arbitraire pour le courant.
Supposons qu'il circule de a vers b dans l'impédance (Fig. 24-24a). En utilisant la première loi de Kirchhoff, et en décrivant la boucle dans le sens horaire, on peut écrire :
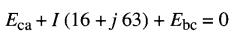
donc
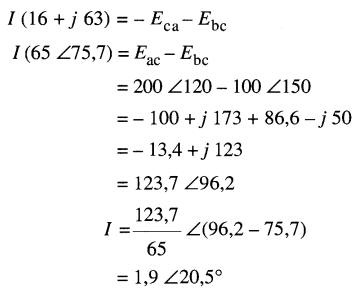
b) Le diagramme vectoriel de Eac, Ebc et I est montré à la Fig. 24-24b.
Figure 24-24b Relations vectorielles (exemple 24-9)
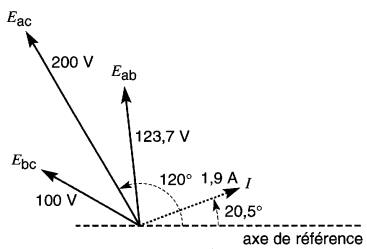
Le courant est en retard sur Eac de 120° -20,5° = 99,5°.
c) On a Eca + Eab + Ebc = 0 donc
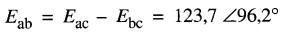
Exemple 24-10
Soit le circuit de la Fig. 24-25a,
Figure 24-25a
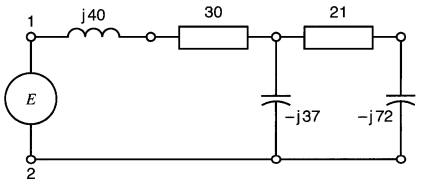
alimenté par une source
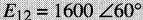
Calculer:
a) le courant dans chaque élément
b) la tension aux bornes de Xc = -j72
Solution
Identifions d'abord les noeuds du circuit, soient les points 3, 4, 5 (Fig. 24-25b).
Fig. 24-25b Résolution du circuit ; choix du sens arbitraire des courants
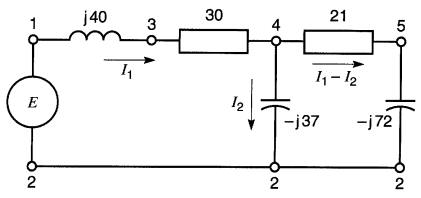
On choisit ensuite un sens arbitraire pour les courants Il et 12; Il circule du noeud 1 au nceud 4, 12 circule du noeud 4 au noeud 2.
D'après la 2e loi de Kirchhoff, le courant circulant dans la branche 4 - 5 - 2 aura comme valeur I1 - I2.
En suivant la première boucle dans le sens horaire, on écrit:
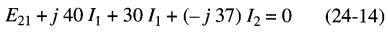
Ensuivant la deuxième boucle dans le sens horaire, on obtient:
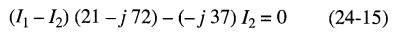
De l'équation 24-14 on obtient :
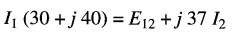
d'où
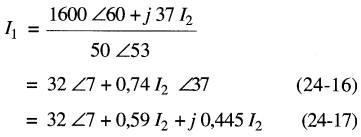
En substituant (24-17) dans (24-15) on obtient :
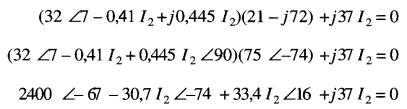
Afin d'additionner les vecteurs, transformons les expressions polaires en forme rectangulaire:
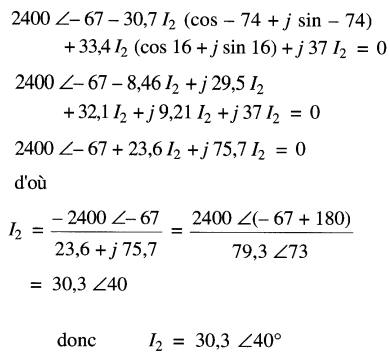
En substituant 12 dans l'équation 24-16 on obtient :
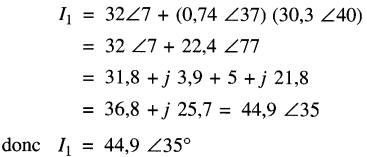
Le courant dans la branche de droite est:
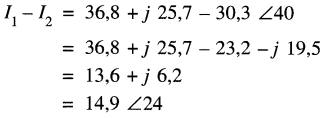
b) La tension aux bornes du condensateur de réactance de Xc = -j72 est:
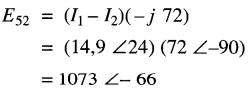
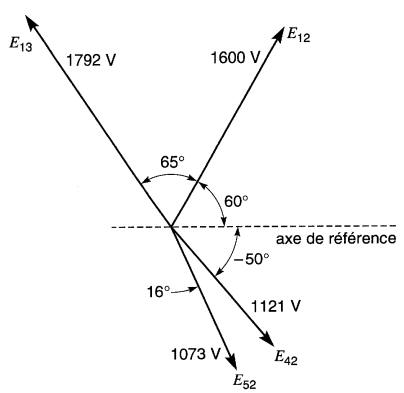
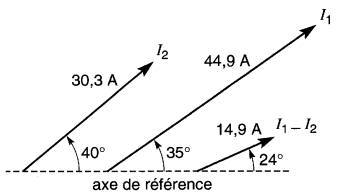
Le diagramme vectoriel complet est donné à la Fig. 24-25c.
Figure 24-25c Relation vectorielle entre les tensions et les courants (voir exemple 24-10)
Notation hybride
Comme nous l'avons signalé à la section 8.9, il est parfois utile d'utiliser simultanément la notation à doubles indices et la notation des polarités pour désigner les tensions.
En voici un exemple.
Exemple 24-11
La Fig. 24-26 montre un circuit triphasé
Figure 24-26 Voir exemple 24-11
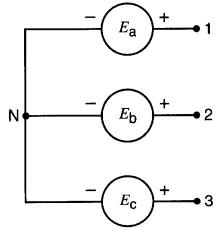
dans lequel
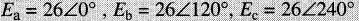(notation des polarités).
Nous désirons calculer la valeur des tensions E12, E23 , et E31 (notation à doubles indices) entre les bornes 1, 2, 3.
Solution
Écrivons les équations de Kirchhoff, en parcourant les boucles respectives dans le sens indiqué :
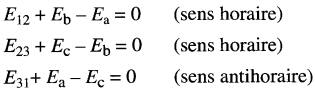
En transposant les termes, on obtient :
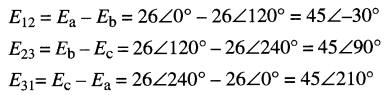
On peut aussi utiliser la notation à doubles indices pour Ea. D'après l'équation de boucle EIN - Ea = 0, on obtient:
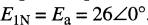
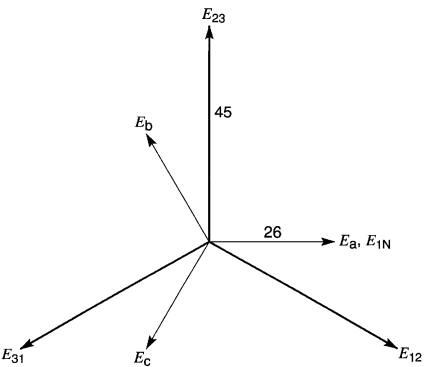
Les différents vecteurs sont montrés à la Fig. 24-27.
Figure 24-27
Résumé
Dans cette section nous avons appris à utiliser trois méthodes de résolution des circuits à courant alternatif la méthode graphique, l'utilisation de formules d'impédance et le calcul vectoriel.
La méthode graphique exige le traçage à l'échelle d'un diagramme vectoriel. Les formules donnant l'impédance de groupements série-parallèle d'éléments R, L, C fournissent une solution rapide mais elles sont limitées aux circuits relativement simples. Le calcul vectoriel est la méthode la plus générale.
Les courants, tensions et résistances qui sont exprimées par de simples nombres dans les circuits à courant continu sont alors remplacés par des vecteurs de tension, courant et impédance.
Selon le type d'opération à effectuer, on exprimera ces vecteurs sous forme polaire ou rectangulaire.
Le calcul vectoriel associé à l'utilisation judicieuse des lois et méthodes apprises pour le courant continu (loi d'Ohm, lois de Kirchhoff, théorème de Thévenin,...) permet de résoudre les circuits à courant alternatif même les plus complexes.
PROBLÈMES
Niveau pratique
24-1 Qu'entend-on par impédance, résistance, réactance d'un circuit?
24-2 Qu'est-ce que la puissance apparente?
24-3 Déterminer la valeur du courant dans les éléments résistif, inductif et capacitif des Fig. 24-28 à 24-31 inclusivement.
Ensuite, en utilisant la méthode graphique, trouver la valeur du courant débité par la source et son déphasage par rapport à la tension.
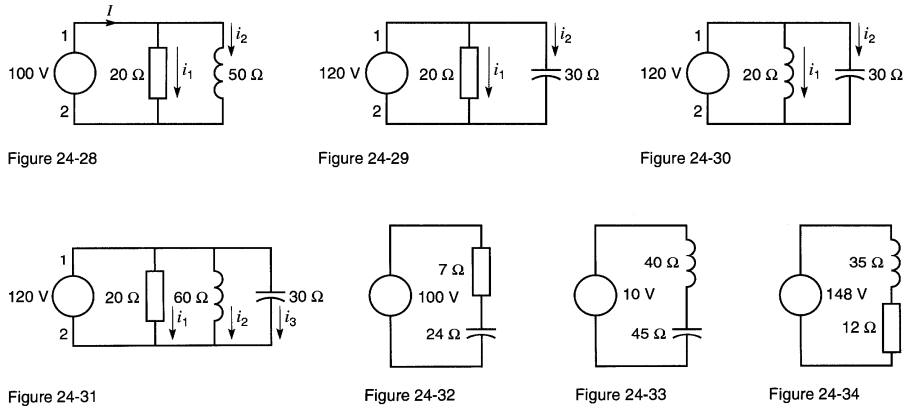
24-4 Dans la Fig. 24-30, quelle réactance inductive doit-on placer en série avec la réactance de 20Ω pour que le circuit devienne résonnant?
24-5 Calculer l'impédance des circuits dans les Fig. 24-28 à 24-31.
Niveau intermédiaire
24-6
a) Déterminer, à l'aide de formules seulement, l'impédance des circuits des Fig. 24-32 à 24-34.
b) Trouver la valeur du courant débité par la source. c) Calculer la tension aux bornes de chaque élément.
24-7
a) Déterminer, à l'aide de formules seulement, l'impédance des circuits des Fig. 24-28 à 24-30.
b) Calculer le courant débité par la source.
24-8 Une bobine possède une inductance de 2H et une résistance de 10Ω.
Quel courant circulera dans la bobine si on la branche:
a) sur une source à c.c. de 600V?
b) sur une source à c.a. de 600V, 60Hz?
24-9
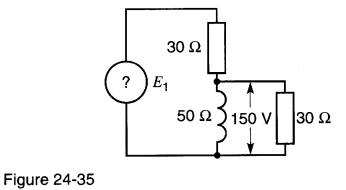
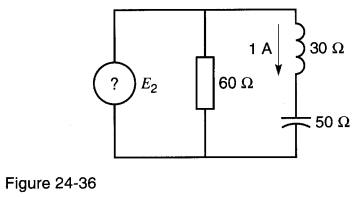
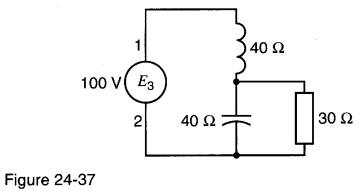
a) Déterminer, par la méthode graphique, les tensions et les courants dans chaque élément des circuits des Fig. 24-35 à 24-37.
b) Trouver le déphasage entre le courant de la source et la tension de la source.
24-10 Un condensateur de 30 µF est raccordé en série avec une résistance de 80Ω aux bornes d'une source de 240V à fréquence variable.
Déterminer le courant de la source et la tension aux bornes du condensateur lorsque la fréquence est de:
a) 60 Hz b) 600 Hz c) 6 Hz d) 0 Hz
Niveau avancé
24-11 Un condensateur de 10 µF est raccordé en série avec une bobine.
Quelle doit être l'inductance de la bobine pour que la résonance se produise à une fréquence de 180 Hz?
24-12 Dans la Fig. 24-16, la réactance capacitive est modifiée à 60 S2. Calculer la valeur du courant ainsi que la tension aux bornes de la bobine. 24-13 Une impédance Z est décrite par l'expression Z=30-j80. a) De quoi est-elle composée: R, L, ou C? b) Exprimer l'impédance dans la forme polaire. 24-14 Dans la Fig. 24-28, déterminer la valeur et l'angle de phase de I en utilisant le calcul vectoriel. La tension E12 de la source est de 100 L 0° volts. 24-15 Dans la Fig. 24-37, calculer la valeur et l'angle de phase du courant dans la résistance de 30 S2, en utilisant le calcul vectoriel. La tension E12 de la source est de 100 Z 0° volts.
24-16 Dans la Fig. 24-38,
Figure 24-38
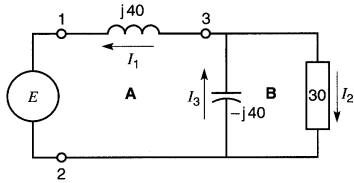
on adonné des directions arbitraires aux courants I1, I2, I3.
Sachant que
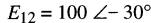
a) écrire les équations du circuit pour les boucles A et B en utilisant la première loi de Kirchhoff
b) écrire l'équation reliant les courants (deuxième loi de Kirchhoff)
c) résoudre le circuit et trouver les valeurs et les angles de phase de E12, E13, E32, I1, I2, I3.
d) tracer le diagramme vectoriel montrant E12, E32et les trois courants
24-17 En se référant à la Fig. 24-39,
Figure 24-39
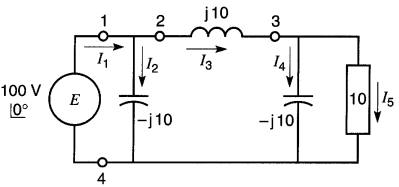
et en utilisant le calcul vectoriel, déterminer la valeur de l'impédance
a) à la droite des points 3, 4
b) à la droite des points 2, 4
c) à la droite des points 1, 4
d) Quelle est la nature de l'impédance aux bornes de la source?
e) Sachant que
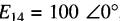
calculer la valeur du courant I1 et tracer le diagramme vectoriel, en montrant seulement les vecteurs E14, I1 et 12.
24-18 En se basant sur les résultats obtenus dans le problème 24-17, calculer, pour le circuit de la Fig. 24-39, la valeur de I3 et de E34.
Exprimer ces deux vecteurs sous la forme polaire. Ensuite, déterminer la valeur des courants I4 et I5. Tracer le diagramme vectoriel du circuit au complet.
24-19 En se basant sur les résultats obtenus dans les problèmes 24-17 et 24-18, et en se référant à la Fig. 24-40
Figure 24-40
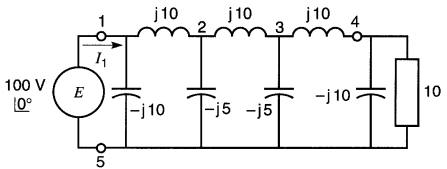
déterminer
a) la valeur de l'impédance aux bornes de la source
b) la valeur et l'angle de phase du courant I1
c) la valeur de la tension aux bornes de la charge
d) l'angle entre la tension E15 de la source et la tension E45 aux bornes de la charge
24-20 La ligne haute-tension à c.c. qui alimente le poste de transformation Dorsey à Winnipeg comprend un filtre L-C-R composé d'une inductance de 0,244 H, d'un condensateur de 0,2 µF, et d'une résistance de 11,05Ω raccordés en série.
À quelle fréquence l'impédance est-elle minimale?
Réponses
3) Figure 24-26: 5 A; 2A;
5,38 A à - 21,8°; Figure 24-27: 6 A; 4 A;
7,21 A à + 33,7°; Figure 24-28: 6
A; 4 A; 2 A à - 90°; Figure 24-29
6 A; 2 A; 4 A; 6,32 A à + 18,4°; 4) 10 4;
5) 18,6 4; 16,6Ω; 60Ω;
19Ω
6a) 25Ω; 5Ω;
37Ω; 6b) 4 A; 2 A; 4 A; 6c) Figure 24-30 : 28 V, 96
V
Figure 24-31: 80 V; 90 V; Figure 24-32: 140V; 48 V;
7a) voir 24-5; 7b)
voir 24-3; 8a) 60 A; 8b) 0,8 A; 9a) Figure 24-33
174,9 V; 313,8 V; 5,83 A;
Figure 24-34:30 V; 50 V; 2 A; 1,05 A;
Figure 24-35:125 V; 75 V; 3,125 A; 9b)
Figure 24-33:-13,9';
Figure 24-34: + 71,6°; Figure 24-35: - 53,1'; Figure
24-36: 0,33 A;
10a) 2 A; 178 V; 10b) 2,98 A; 26,3 V; 10c) 0,27A; 239 V;
10d) 0 A; 240 V; 11) 78,2 mH; 12) 2,91 A; 291 V; 13a) R et C;
13b) 85,4
Ω à -69,4°; 14) 5,38 A à - 21,8°; 15) 2,5 A à - 90°;
16c) 3,125 A à
96,9°; 2,5 A à -120°; 1,875 A à 150°;
E13 = 125 V à 6,9°; E32 = 75 V à -120°;
17a) 5 - j 5; 17b) 5 + j 5;
17c) 10
Ω; 17d) résistive; 17e) 10 A à 0°;
18) 14,14 A à - 45°; 10 A à 0°; 10
A à - 90°; E34 = 100 V à - 90°;
19a) 10 52; 19b) 10 A à 0°; 19c) 100 V à
+ 90° ; 19d) 270°;
20) 720 Hz; 12e harmonique
