Puissance active, réactive et apparente

Électrotechnique

En électrotechnique, les concepts de puissance active, de puissance réactive et de puissance apparente est d'une importance capitale.

Nous verrons que, bien souvent, il est plus facile d'expliquer les phénomènes électriques en travaillant avec les puissances plutôt qu'avec les tensions et les courants.

Dans les explications qui suivent, on doit se rappeler que les puissances active, réactive et apparente s'appliquent seulement aux circuits à courant alternatif fonctionnant en régime permanent et dont les formes d'ondes sont sinusoïdales. Le lecteur aurait avantage à revoir brièvement la section Circuits simples à courant alternatif traitant des circuits à c.a. simples.

On y a vu qu'une puissance active nécessite une consommation d'énergie électrique. Par contre, une puissance réactive n'est associée à aucune dépense d'énergie.

Notions préliminaires

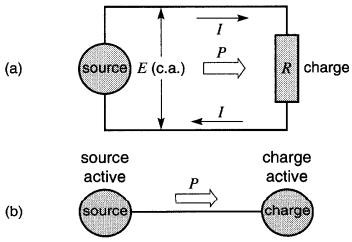
Le circuit de la Fig. 25-1a représente un système à courant alternatif comprenant une source et une charge raccordées par deux fils conducteurs.

 Figure 25-1

a. La puissance active est transportée par les deux conducteurs;

b. Schéma unifilaire. Une seule ligne représente le câble entre la source et la charge.

La charge consomme une puissance active P. Si ce réseau fonctionne à 60 Hz, la tension change de polarité et le courant change de sens 60 fois par seconde.

Par contre, la puissance active se dirige constamment de la source vers la charge. La direction de la puissance active est montrée par une flèche P.

Cette puissance est transportée par l'ensemble des deux fils conducteurs, c'est-à-dire par le câble reliant la source et la charge.

Pour cette raison, lorsqu'on s'intéresse au transport de puissance, il est préférable (et plus simple) de dessiner une seule ligne entre la source et la charge, cette ligne pouvant représenter deux ou plusieurs fils conducteurs (Fig. 25-1b).

Ce circuit simplifié à un seul fil porte le nom de schéma unifilaire. On peut, de la même façon, montrer le transport d'une puissance réactive Q entre une source et une charge.

La source et la charge sont alors nommées respectivement «source réactive» et «charge réactive» et une flèche Q se dirige de la source vers la charge (Fig. 25-2).

Figure 25-2 Schéma unifilaire du circuit de la Fig. 25-1. La puissance réactive est transportée par le câble

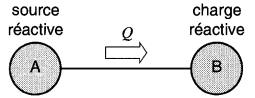
Il arrive souvent qu'un dispositif B (Fig. 25-3) absorbe simultanément une puissance active et une puissance réactive; dans ce cas, les flèches Pet Q se dirigent dans le même sens.

Figure 25-3 Puissance active et réactive circulant dans le même sens

Dans cette figure, B est à la fois une charge active et une charge réactive. Dans d'autres cas, les puissances active et réactive se dirigent en sens inverses, comme l'indique la Fig. 25-4.

Figure 25-4 Puissance active et réactive circulant en sens contraires

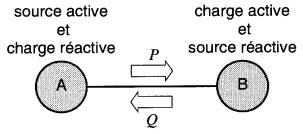
Dans cette figure, A est à la fois une source active et une charge réactive. II peut paraître surprenant que deux puissances puissent circuler en sens inverse dans un même câble, mais il faut se rappeler qu'une puissance active P n'est pas de même nature qu'une puissance réactive Q et que Tune et l'autre peuvent être traitées séparément.

Sources et charges actives

La plupart des sources actives sont des générateurs à courant alternatif, ou alternateurs. Une prise de courant constitue aussi, en quelque sorte, une source active car elle est effectivement branchée à un alternateur, aussi éloigné soit-il. La plupart des charges actives sont des moteurs électriques à courant alternatif fournissant une puissance mécanique, et des éléments résistifs dégageant de la chaleur.

À ceux-ci, il faut ajouter les convertisseurs électroniques servant à transformer le courant alternatif en courant continu. La propriété unique d'une puissance active est de faire un travail.

La Fig. 25-5a montre deux dispositifs reliés ensemble dont les bornes sont a et b et dont le courant I circule dans le sens indiqué.

Figure 25-5 Définitions d'une source et d'une charge actives

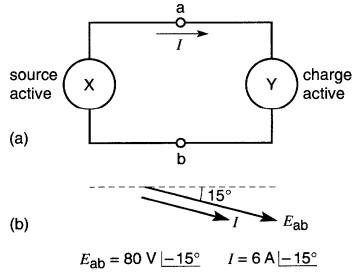
Par définition, un dispositif ayant deux bornes a et b absorbe une puissance purement active lorsque le courant I entrant dans la borne a du dispositif est en phase avec la tension E_ab. Le dispositif est alors une charge active.

Cette définition de la charge active en entraîne naturellement une autre pour la source active:

Un dispositif ayant deux bornes a et b débite une puissance purement active lorsque le courant I sortant de la borne a du dispositif est en phase avec la tension E_ab. Le dispositif est alors une source active.

Par exemple, supposons que dans un cas particulier on trouve que

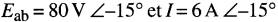(Fig. 25-5b).

Selon cette information, et d'après nos définitions, Y est une charge active et X est une source active. Le même diagramme vectoriel s'applique à la source X, à la charge Y et à la ligne qui les relie.

La puissance active se mesure en watts (W), en kilowatts (kW) ou en mégawatts (MW).

Sources et charges réactives

Les principales sources de puissance réactive sont les alternateurs et les condensateurs. Il n'est pas surprenant qu'un alternateur qui tourne soit capable de fournir ce genre de puissance, mais il est tout à fait inattendu qu'un élément passif comme un condensateur puisse se comporter comme une source.

Rappelons, cependant, qu'une puissance réactive ne requiert aucune énergie électrique (joules). Elle représente en effet de l'énergie qui oscille sur une ligne électrique tantôt dans un sens, tantôt dans le sens inverse.

Par conséquent, l'énergie fournie par le condensateur est, en moyenne, nulle. Toutefois, même si l'énergie change de sens périodiquement, il est utile de conserver les concepts de «source» et de «charge» pour la puissance réactive.

En électrotechnique, les condensateurs sont toujours considérés comme des sources de puissance réactive. La plupart des charges réactives sont des enroulements qui produisent un champ magnétique alternatif. Tout comme une puissance active fait un travail, une puissance réactive produit un champ magnétique alternatif. C'est dire que tout dispositif nécessitant un champ alternatif, comme les bobines, les moteurs, les relais, les électro-aimants, absorbe une puissance réactive.

Toutefois, des puissances réactives sont aussi mises en jeu lorsque le courant dans un circuit est retardé ou avancé par l'action d'un ou de plusieurs interrupteurs électroniques.

La Fig. 25-6a montre deux dispositifs reliés ensemble dont les bornes sont a et b et dont le courant I circule dans le sens indiqué.

Figure 25-6 Définitions d'une source et d'une charge réactives

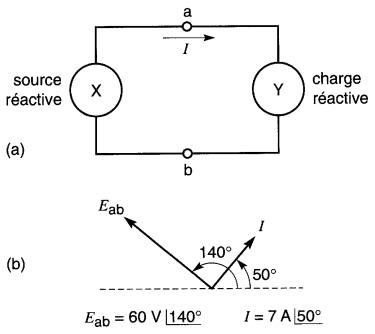
Par définition, un dispositif ayant deux bornes a et b absorbe une puissance purement réactive lorsque le courant I entrant dans la borne a du dispositif est 90° en arrière de la tension E_ab. Le dispositif est alors une charge réactive.

Note: L'interprétation que nous donnons ici de la puissance réactive est conforme à la définition donnée par l'IEEE.

Cette définition de la charge réactive en entraîne naturellement une autre pour la source réactive: Un dispositif ayant deux bornes a et b débite une puissance purement réactive lorsque le courant I sortant de la borne a du dispositif est 90° en arrière de la tension E_ab. Le dispositif est alors une source réactive.

Par exemple, supposons que dans un cas particulier

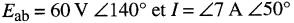  (Fig. 25-6b).

Selon cette information, et d'après nos définitions, Y est une charge réactive et X est une source réactive. Le même diagramme vectoriel s'applique à la source X, à la charge Y et à la ligne qui les relie.

La puissance réactive se mesure en vars (var), en kilovars (kvar) ou en mégavars (Mvar).

Dans le cas général d'un dispositif où la tension et le courant ne sont pas parfaitement en phase ou en quadrature, ce dispositif absorbe ou génère simultanément une puissance active et une puissance réactive. Dans ce cas, on doit procéder comme expliqué à l'exemple ci-dessous pour trouver la puissance active et la puissance réactive.

Exemple 25-1

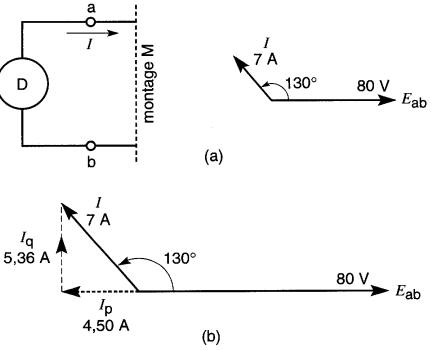
Un dispositif D raccordé à un montage M porte un courant I de 7A déphasé de 130" en avance sur la tension E_ab (Fig. 25-7a).

Figure 25-7 Voir exemple 25-1

 Déterminez la nature des puissances actives et réactives mises enjeu.

Solution

Décomposons le courant I en deux vecteurs Ip et Iq respectivement en ligne et en quadrature avec la tension E_ab (Fig. 25-7b).

On obtient les résultats suivants:

1) Valeur de Ip = 7 cos 130° =-4,50A. Ce courant est donc déphasé de 180° par rapport à E_ab.

2) Selon nos définitions, si Ip était en phase avec E_ab, le montage M serait une charge active. Comme c'est le cas contraire, M est une source active; par conséquent, D est une charge active. La puissance active absorbée par D est donc:

 P= EI = 80V x 4,50A = 360W

3) Valeur de Iq = 7 sin 130° = 5,36 A.

Ce courant est déphasé de 90° en avance sur E_ab.

4) Selon nos définitions, si Iq était 90° en arrière de E_ab, le montage M serait une charge réactive.

Comme c'est le cas contraire, M est une source réactive. Par conséquent, D est une charge réactive. La puissance réactive absorbée par D est donc :

Q= EI = 80V x 5,36A = 429 var

Mesure de la puissance active et réactive

Pour mesurer la puissance active dans un circuit, on utilise un wattmètre. Cet instrument (Fig. 25-8) possède 4 bornes : deux pour mesurer la tension et deux pour mesurer le courant.

Figure25-8 Wattmètre de haute précision à échelles multiples; tensions: 50V. 100 V, 200 V courants: 1 A, 5 A. Échelles de puissance: 0W à 50 W jusqu'à 0 à 1000 W

Une des bornes de tension est marquée d'un signe (±), de même qu'une des bornes de courant. Un wattmètre peut donc être considéré comme un voltmètre et un ampèremètre combinés dans le même boîtier.

La résistance entre les bornes de courant est très faible, tandis que celle entre les bornes de tension est très élevée. La tension et le courant maximum que l'instrument peut supporter sont toujours indiqués.

La Fig. 25-9 montre comment on doit raccorder le wattmètre dans un circuit monophasé.

Figure 25-9 Méthode de raccordement d'un wattmètre (ou d'un varmètre) dans un circuit monophasé

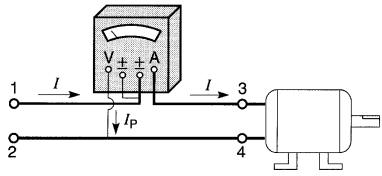
Lorsque la puissance active circule des bornes 1, 2 (côté source) vers les bornes 3, 4 (côté charge), l'aiguille dévie dans le bon sens.

Par contre, si la puissance circule dans le sens inverse, l'aiguille se déplace vers la gauche, ce qui rend la lecture impossible. On peut mesurer cette puissance négative en intervertissant les deux fils connectés aux bornes de tension.

Pour mesurer la puissance réactive dans un circuit, on utilise un varmètre (Fig. 25-10). Sa construction est similaire à celle d'un wattmètre et il est raccordé dans un circuit exactement de la même manière (Fig. 25-9).

Figure 25-10 Varmètre pouvant afficher une puissance réactive positive et négative

Si l'aiguille se déplace vers la droite, cela indique que la puissance réactive circule des bornes 1, 2 vers les bornes 3, 4.

Par contre, si la puissance circule dans le sens inverse, on doit intervertir les deux fils raccordés aux bornes de tension, afin de prendre la lecture négative. Dans certains modèles, le zéro de l'échelle se trouve au centre du cadran, ce qui permet une lecture de la puissance réactive circulant dans une direction ou l'autre. De nos jours, il existe plusieurs modèles de wattmètres et de varmètres.

Quelques-uns mesurent la puissance par un procédé électromécanique à l'aide d'un enroulement fixe et d'un enroulement mobile et utilisant un cadran à affichage analogique. D'autres modèles contiennent des composants électroniques et un cadran à affichage numérique.

Charges active et réactive - puissance apparente

En général, les charges, comme un moteur, absorbent à la fois une puissance active P et une puissance réactive Q. Considérons, par exemple, le circuit monophasé de la Fig. 25-1 l a composé d'une source G, d'une charge et des instruments de mesure.

Figure 25-11

a. Instruments utilisés pour mesurer les valeurs de E, I, P, Q dans un circuit;

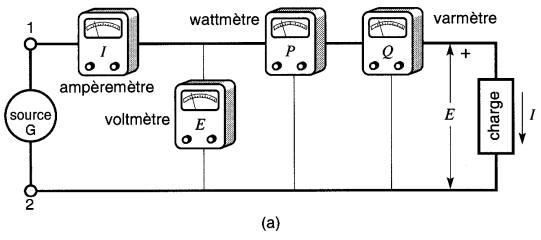
b. Diagramme vectoriel des tensions et courants découlant de la lecture des instruments;

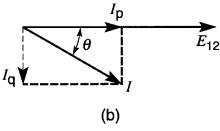
c. La charge industrielle peut être représentée par une résistance en parallèle avec une réactance inductive

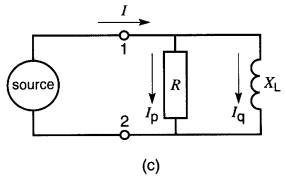
 Supposons que les instruments donnent les lectures suivantes:

voltmètre: E volts, ampèremètre: I, ampères wattmètre: +P watts, varmètre: +Q vars

Puisque les puissances P et Q sont positives, il s'ensuit que la charge absorbe de la puissance active et réactive. Par conséquent, le courant I dans la ligne est déphasé en arrière de la tension d'un angle θ.

On peut décomposer ce courant en deux composantes, soient les vecteurs I_p et I_q, qui sont respectivement en phase, et 90° en arrière du vecteur E₁₂ (Fig. 25-1 lb).

On peut donc représenter la charge par une résistance R en parallèle avec une réactance inductive X_L (Fig. 25-11c). La résistance tire un courant I_p tandis que la réactance tire un courant I_p.

Il est évident que:

I² = I²_p + I²_p     (25-1)

On peut calculer les valeurs de I_p et de I_p à partir des lectures des instruments:

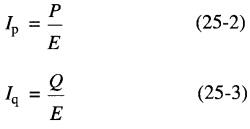
Par définition, la puissance apparente du circuit est donnée par

S = EI (éq. 24-2), d'où:

I = S / E  (25-4)

Sachant que

I² = I²_p + I²_p

On peut écrire:

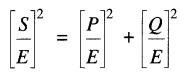
où

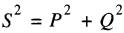  (25-5)

ou

S = puissance apparente, en volts-ampères [VA]

P = puissance active, en watts [W]

Q = puissance réactive, en vars [var]

On peut représenter la relation entre P, Q, S par le triangle de la Fig. 25-12, parfois appelé triangle de puissance. Les puissances respectives sont représentées par des vecteurs P, Q, S.

Figure 25-12 Relation graphique entre les vecteurs de puissance pour un des positif qui absorbe une puissance active P et une puissance réactive Q

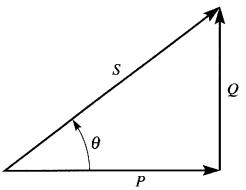
Voici comment on interprète ces vecteurs: 

1) Dans le cas d'une charge qui absorbe une puissance active, le vecteur P est tracé vers la droite.

2) Dans le cas d'une charge qui absorbe une puissance réactive, le vecteur Q est tracé vers le haut.

3) Dans le cas d'une source qui débite une puissance active, le vecteur P est tracé vers la gauche.

4) Dans le cas d'une source qui débite une puissance réactive, le vecteur Q est tracé vers le bas.

Exemple 25-2

Un moteur à courant alternatif absorbe une puissance active de 40 kW et une puissance réactive de 30 kvar. Calculer la valeur de la puissance apparente fournie moteur.

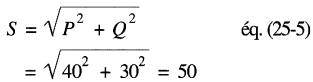
La puissance apparente est de 50 kVA

Facteur de puissance

Le facteur de puissance d'un circuit alternatif est donné par l'expression :

FP = P / S    (25-6)

où

FP = facteur de puissance, exprimé par un simple nombre sans dimension, ou en pourcent

P = puissance active du circuit, en watts [W]

S = puissance apparente du circuit, en volts-ampères [VA]

Étant donné que la puissance active P ne peut jamais être supérieure à la puissance apparente, il s'ensuit que le facteur de puissance ne peut pas excéder une valeur de 1 (ou 100 %). Le FP d'une résistance est de 100 % car sa puissance apparente est égale à sa puissance active. Le FP d'une bobine idéale est nul car elle ne consomme aucune puissance active.

En somme, le facteur de puissance d'un circuit est simplement un nombre indiquant le pourcentage de la puissance apparente qui est active. Le facteur de puissance donne une autre information utile.

En se référant à la Fig. 25-11b, on peut écrire:

I_p = Icosθ

En multipliant les deux côtés de l'équation par la tension efficace E de la source, on obtient:

EI_p = EIcosθ soit P = Scosθ

Puisque le rapport P / S = facteur de puissance, il s'ensuit que:

FP = cosθ    (25-7)

d'où θ = arccos FP

Donc, si l'on connaît le facteur de puissance d'un circuit, on connaît le déphasage entre la tension d'alimentation et le courant de ligne.

Étant donné que le courant peut être en avance ou en retard sur la tension, on qualifie le FP de la manière suivante:

le FP est dit en retard lorsque le courant est en retard sur la tension;

le FP est dit en avance lorsque le courant est en avance sur la tension.

La Fig. 25-13 montre un instrument permettant de mesurer le facteur de puissance dans une usine.

Figure 25-13 Instrument mesurant le facteur de puissance en avance ou en retard. Lorsque l'aiguille est au centre de l'échelle, le facteur de puissance est de 1 ou 100 %

Exemple 25-3

a) Dans l'exemple 25-2, calculer le facteur de puissance du moteur et indiquer s'il est en avance ou en retard.

b) Calculer l'angle entre la tension et le courant.

Solution

a) Le facteur de puissance est donné par:

FP = P / S = 40 Kw / 50 KVA = 0.8 = 8%

Donc 80 % de la puissance apparente fournie au moteur est une puissance active.

Le facteur de puissance est en retard parce que, dans le cas d'un moteur, le courant est en arrière de la tension.

b) L'angle de déphasage est:

θ = arccos FP = arccos 0,8 = 36,9°

Exemple 25-4

Un wattmètre et an varmètre sont raccordés dans une ligne à 120 V alimentant un moteur. Les instruments indiquent respectivement 1800 W et 960 var.

Calculer:

a) les composants I_p et I_q du courant

b) la valeur du courant dans la ligne

c) la puissance apparente fournie au moteur

d) le facteur de puissance du moteur

e) l'angle de déphasage entre la tension et le courant de ligne

Solution

a) En se référant à la Fig. 25-11, où la charge est maintenant un moteur, on a :

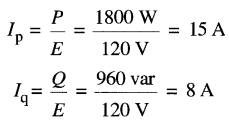
b) Du diagramme vectoriel on tire:

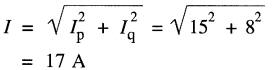
c) La puissance apparente est :

S = EI = 120 x 17 = 2040 VA

d) Le FP est:

FP = P / S = 1800 W / 2040 VA = 0,882 ou 88,2 %

e) l'angle de déphasage est:

θ = arccos FP = arccos 0,882 = 28,1°

Amélioration du facteur de puissance

Considérons un moteur raccordé à une source par l'entremise d'une ligne a3, b4 d'une longueur de quelques dizaines de mètres (Fig. 25-14).

Figure 25-14 Puissances active et réactive transportées par une ligne ayant une longueur de plusieurs mètres

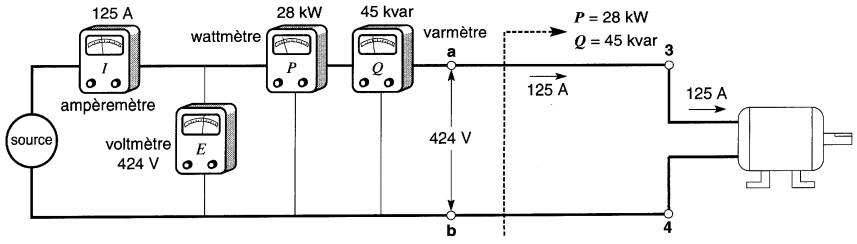
Un groupe d'instruments sert à mesurer les grandeurs électriques. La tension est de 424V et le courant de ligne est de 125A.

 De plus, on observe que le moteur absorbe une puissance active de 28 kW et une puissance réactive de45 kvar.

Un calcul rapide révèle que la source fournit une puissance apparente de 424V x 125A = 53 kVA à un facteur de puissance de 28 kW/53 kVA = 0,528 = 52,8 %, en retard.

La ligne reliant la source et la charge porte donc une paissance oscillatoire «inutile» de 45 kvar en même temps qu'elle transporte la puissance utile de 28 kW. Le transport de cette puissance réactive impose un échauffement supplémentaire aux conducteurs de ligne.

Comme la ligne est assez longue, la circulation de la puissance réactive peut occasionner des pertes Joule importantes.

Comment peut-on remédier à cette situation?

On se souvient qu'un condensateur est une source de puissance réactive. Par conséquent, un condensateur branché en bout de la ligne, directement aux bornes 3, 4 du moteur, pourrait fournir une partie ou même toute la puissance réactive dont le moteur a besoin.

Supposons que le condensateur génère exactement 45 kvar (Fig. 25-15).

Figure 25-15 un condensateur branché aux bornes de la charge diminue la puissance apparente transportée par la ligne

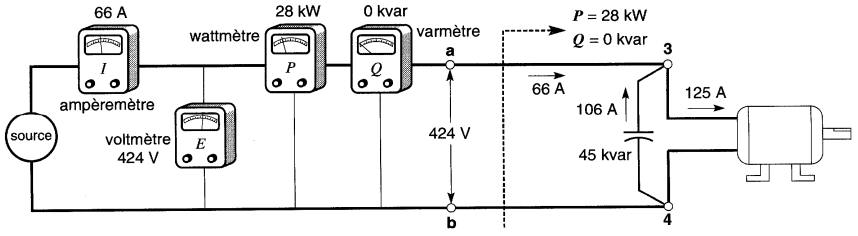
Dans ce cas, la puissance réactive fournie par la source tombe à zéro, car toute la puissance réactive est maintenant générée localement. La puissance active fournie par la source demeure inchangée parce que le moteur développe toujours la même puissance mécanique.

Comme la source fournit seulement 28 kW, il s'ensuit que le courant dans la ligne tombe de 125A à:

I = P / E = 28kW / 424V = 66A

Cette réduction importante du courant de ligne diminue l'échauffement des conducteurs de plus de 70 %. De plus, la source doit seulement fournir une puissance active de 28 kW, au lieu d'une puissance apparente de 53 kVA.

En effet, la source «voit» maintenant une charge dont le FP est de 100 %, alors qu'il était auparavant de 52,8 %.

Notons que le facteur de puissance du moteur n'a pas changé; il est encore de 52,8 %, et il tire toujours un courant de 125A (Fig. 25-15).

Le condensateur fournit un courant de:

I = Q / E = 45 kvar / 424v = 106A

Sa réactance capacitive est donc:

X_c = E / I = 424v / 106A = 4Ω

En utilisant la formule 22-6, on trouve la capacitance du condensateur:

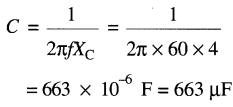
En général, on cherche à placer les condensateurs le plus près possible des charges réactives inductives, afin de réduire le courant dans les lignes. Nous verrons à la section Moteurs monophasés que l'amélioration (ou «correction») du facteur de puissance qui en résulte a une influence importante sur la tarification de l'électricité.

Systèmes comprenant plusieurs charges

Les notions de puissances active et réactive permettent de simplifier la résolution des circuits complexes. Considérons, par exemple, le système de charges raccordées selon la Fig. 25-16 et alimentées par une source de 380V.

Figure 25-16 Système complexe composé de plusieurs charges raccordé à une source de 380V

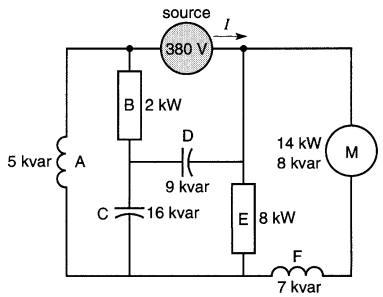
On veut calculer la puissance apparente fournie par la source d'alimentation, ainsi que le courant qu'elle débite.

En utilisant la méthode des puissances, on n'a plus besoin de se préoccuper du raccordement entre les charges. Il suffit de tracer un simple schéma unifilaire (Fig. 25-17)

Figure 25-17 Simplification du montage utilisant le concept des puissances active et réactive

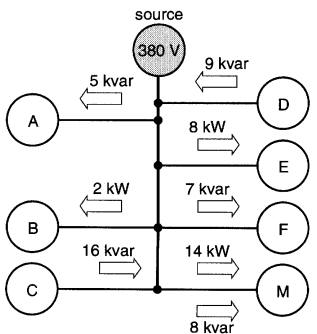
et d'additionner les puissances actives et réactives associées aux divers éléments, comme suit:

1. Puissance active absorbée par les éléments B, E, M :

P=(+2+8+14) =+24 kW

2. Puissance réactive absorbée par les éléments A, F, M :

Q₁ = (+ 5 + 7 + 8) = +20 kvar

3. Puissance réactive débitée par les condensateurs C, D:

Q₂ = (-9 - 16) = -25 kvar

4. Puissance réactive nette absorbée par le système:

Q = Q₁ + Q₂ = (+20 - 25) = -5 kvar

5. Puissance apparente fournie au système :

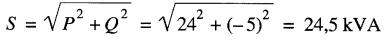
6. La tension de la source d'alimentation étant de 380V le courant I vaut:

I = S / E = 24 500 VA / 380V = 64,5A

La Fig. 25-18 montre les vecteurs des puissances actives et réactives mises en jeu.

Figure 25-18 Représentation graphique des puissances active et réactive et de la puissance apparente du système de la Fig. 25-16

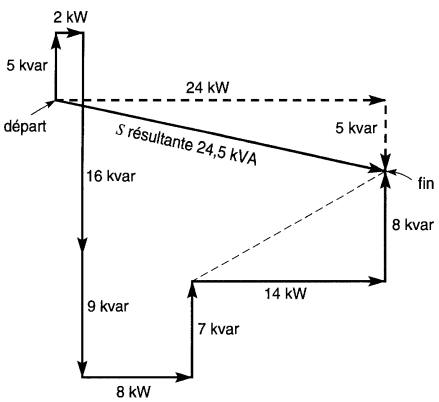
Cette figure fournit une solution graphique du problème. En commençant par le vecteur de puissance réactive de 5 kvar, on dessine, à l'échelle, la grandeur de chacun des vecteurs de puissance. Chaque vecteur de puissance active est tracé à l'horizontale, vers la droite ou vers la gauche selon son signe.

De même, chaque vecteur de puissance réactive est dessiné à la verticale, vers le haut ou vers le bas, selon son signe. Une fois les vecteurs ajoutés les uns à la suite des autres, on relie le point de départ au point final, ce qui donne un vecteur incliné dont la longueur correspond à 24,5 kVA.

La composante horizontale de ce vecteur est de 2.4 kW; comme il est dirigé vers la droite, il représente une puissance active absorbée par l'ensemble des charges. La composante verticale est de 5 kvar. Puisque ce vecteur de puissance réactive est dirigé vers le bas, il représente une puissance réactive débitée par l'ensemble des charges.

Comme autre exemple, considérons le circuit de la Fig. 25-19 composé d'une charge résistive de 24 kW en parallèle avec une «charge» capacitive de 7 kvar, le tout alimenté par une prise de courant (réceptacle) de 600 V. Le réceptacle débite une puissance active de 24 kW qui se trouve dissipée dans la résistance.

Figure 25-19 a. Effet d'un condensateur branché sur un réceptacle. b. Direction des puissances active et réactive

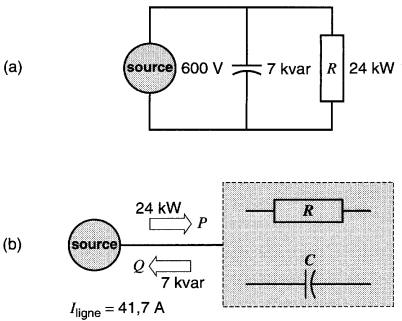
Par contre, il reçoit une puissance réactive de 7 kvar générée par le condensateur. Cette puissance réactive entre dans la prise de courant et devient disponible sur le grand réseau de la compagnie d'électricité. La puissance apparente associée à la charge est:

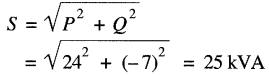
Le courant de la source d'alimentation vaut donc

I = S/E = 25 000/600 = 41,7 A

Résolution des circuits par la méthode des puissances

Le concept des puissances active et réactive peut servir à résoudre des circuits à courant alternatif. Il suffit de calculer les puissances associées aux divers éléments. En utilisant cette méthode, on peut souvent résoudre des circuits assez compliqués sans même tracer un diagramme vectoriel.

En voici deux exemples.

Exemple 25-5

Trouver l'impédance du circuit de la ig. 25-20a.

Figure 25-20a Montage série-parallèle dont on cherche l'impédance

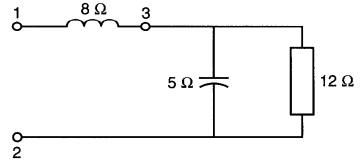
Solution

L'impédance du circuit ne dépend pas de la tension qu'on lui applique. On peut donc supposer une tension quelconque aux bornes d'un élément approprié et, par déductions successives, déterminer les tensions et les courants dans tous les autres éléments.

Supposons donc une tension de 60V entre les points 3 et 2 (Fig. 25-20b).

Figure 25-20b Résolution du circuit par la méthode des puissances

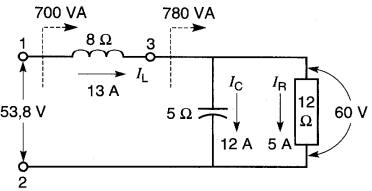
On a:

1. I_c = 60V / 5Ω =12A.

Comme le condensateur est une source de puissance réactive, on a:

Q_c = -(12 A x 60V) = -720 var

2.I_R = 60V / 12Ω = 5A d'où P= 5A x 60V = +300W

3. puissance apparente associée au circuit entre les points 3 et 2:

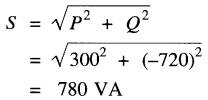
4. courant

I_L= S/E₃₂ = 780/60 = 13A

5. tension aux bornes de la réactance:

E₁₃ = X_LI_L = 8Ω x 13A = 104V

6. puissance réactive absorbée par la réactance :

Q_L = E₁₃ X I_L = 104V x 13A = + 1352 var

7. puissance réactive totale absorbée par le circuit entre les points 1 et 2:

Q = 1352 + (-720) = +632 var

8. puissance active totale absorbée par le circuit entre les points 1 et 2:

P=+300W

9. puissance apparente associée au circuit entre les points 1 et 2:

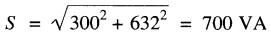
10. tension E₁₂ = S/I_L = 700/13 = 53,8 V

11. impédance vue entre les points 1 et 2

Z= E₁₂ / I_L = 53,8 / 13 = 4,14Ω

Exemple 25-6

l'exemple 25-5. déterminer le courant circulant dans la résistance lorsque E₁₂ = 300 V.

Solution

Une simple règle de trois permet de calculer le courant. En effet, comme une tension de 53,8V entre les bornes 1 et 2 produit un courant de 5A dans la résistance, une tension de 300V donnera:

I_R = 5A x 300/ 53,8 = 27,9A

Exemple 25-7

Une ligne monophasée à 12.47 kV partant d'un poste de transformation alimente une charge située quelques kilomètres plus loin (Fig. 25-21 ).

Figure 25-21 Ligne longue transportant une puissance importante (voir exemple 25-7)

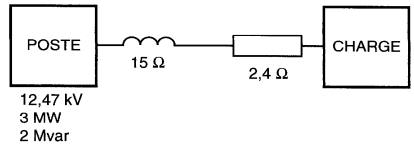
La ligne possède une réactance inductive de 15Ω et une résistance de 2,4Ω. Au poste, les instruments indiquent qu'il débite une puissance active de 3 MW, et une puissance réactive de 2 Mvar.

Calculer:

a) la valeur du courant de ligne et son déphasage par rapport à la tension au poste

b) la puissance active absorbée par la charge

c) la puissance réactive absorbée par la charge

d) la tension aux bornes de la charge

e) l'angle (le déphasage entre la tension au poste et celle aux bornes de la charge

Solution

a) Puissance apparente fournie à la ligne:

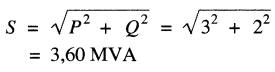
Courant de ligne:

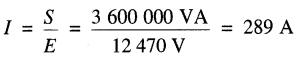
Facteur de puissance au poste:

Angle entre la tension et le courant au poste:

θ = arccos 0,833 = 33,6°

b) Puissance dissipée dans la ligne:

P_L = RI² = 2,4 x 289² = 0,2 x 10⁶ = 0,2 MW

c) Puissance réactive absorbée par la ligne:

Q_L = X_LJ² = 15 x 289² = 1,25 x 106 = 1,25 Mvar

Puissance réactive absorbée par la charge:

QC = Q_poste- Q_L = 2 Mvar - 1,25 Mvar = 0,75 Mvar

d) Puissance apparente de la charge:

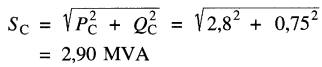
Tension aux bornes de la charge :

Facteur de puissance de la charge :

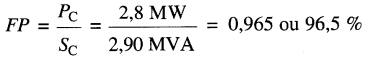
e) Angle entre le courant et la tension aux bornes de la charge:

θc = arccos 0,965 = 15,2 °

Il s'ensuit que la tension aux bornes de la charge est en retard sur celle au poste par (33,6° - 15,2°) = 18,4°. La Fig. 25-22 résume les résultats de cette analyse.

Figure 25-22 Tensions, courants et puissances sur le réseau (voir exemple 25-7)

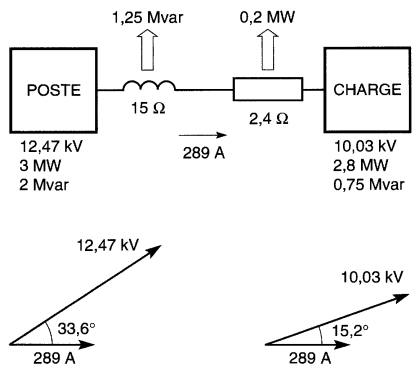
On aurait pu obtenir le même résultat en utilisant le calcul vectoriel, ou une méthode graphique, mais la «méthode des puissances» est d'une simplicité fort attrayante.

Transport de puissances P et Q entre deux sources de tension

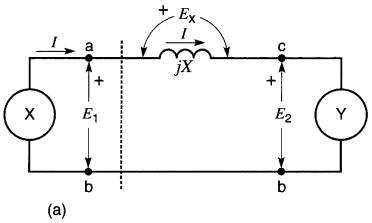
Il arrive assez fréquemment que deux sources d'énergie X et Y soient reliées par une réactance inductive (Fig. 25-23a).

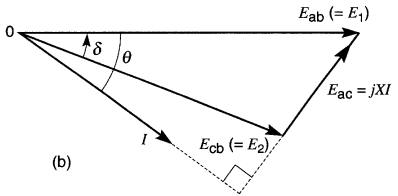
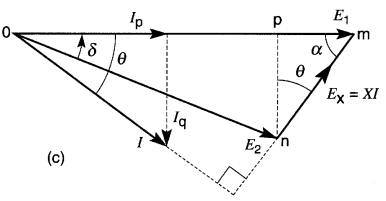
Figure 25-23

a) Échange de puissances entre deux sources X et Y.
b) Diagramme vectoriel des tensions et du courant.
c) Relations géométriques entre les vecteurs.
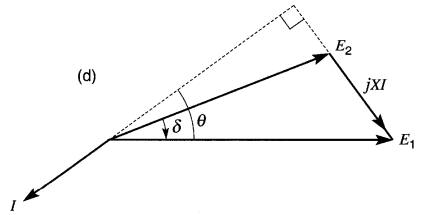
d) Tension E₂ de Y est en avance sur E₁ de X.

On rencontre notamment ce genre de circuit dans l'étude des alternateurs, des moteurs synchrones, des lignes de transport et des convertisseurs statiques de toutes sortes.

Dans ces circuits, une certaine puissance active et réactive est transportée entre les sources. La valeur et la direction des puissances dépendent de l'amplitude des tensions E_ab et E_cb des sources, de l'angle de phase (5 entre ces deux tensions et de la réactance X.

En se référant à la Fig. 25-23a, on peut écrire les équations de Kirchhoff suivantes :

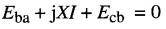
d'où

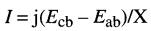
Prenons la tension E_ab comme vecteur de référence, et supposons qu'elle soit déphasée en avance sur E_cb d'un angle θ. On obtient alors le diagramme vectoriel de la Fig. 25-23b.

Dans ce diagramme, le vecteur I est nécessairement perpendiculaire au vecteur E_ac; il est déphasé en arrière du vecteur E_ab d'un angle θ.

Décomposons le courant I en deux vecteurs I_p et I_q, respectivement parallèle et perpendiculaire à la tension E_ab (Fig. 25-22c).

On constate que I_p est en phase avec E_ab et qu'il circule de la borne a vers la borne b. Donc, selon notre définition de la section 25-2, le circuit situé à droite des bornes a et b absorbe une puissance active.

Par conséquent, la source X débite une puissance active donnée par:

P = E_abI_p = E_abICOsθ

On constate aussi que I_q est 90° en arrière de E_ab et que ce courant circule de la borne a vers la borne b.

Donc, selon la définition donnée à la section 25-3, le circuit situé à droite des bornes a et b absorbe une puissance réactive. Par conséquent, la source X débite une puissance réactive donnée par:

Q = E_abI_q = E_abIsinθ

Exprimons maintenant les puissances P et Q en fonction des tensions E_ab, E_cb et de l'angle θ.

Pour ce faire, examinons d'abord les relations géométriques entre les vecteurs de la Fig. 25-23c. Afin d'alléger le texte, remplaçons les tensions Eab, Ecb et jIX par E₁, E₂ et E_x.

Cherchons d'abord une expression pour la puissance active P.

Valeur de la puissance active

On constate que les vecteurs forment un triangle dont les longueurs des côtés om, on et mn sont respectivement E₁, E₂ et E_x (Fig. 25-23c).

À partir du point n, traçons une ligne pointillée np perpendiculaire à la ligne om. On note que l'angle mnp est alors égal à θ. La puissance active débitée par la source X est donnée par:

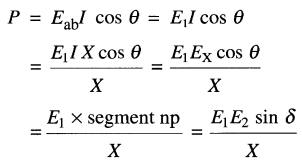
On peut donc écrire:

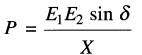    (25-13)

où

P = puissance active débitée ou absorbée par la source X [W]
E₁ = tension efficace de la source X [V]
E₂ = tension efficace de la source Y [V]
δ = angle d'avance de E₁ sur E2
X = réactance reliant les sources X et Y [Ω]

La formule 25-13 est importante car nous aurons l'occasion de l'utiliser à plusieurs reprises dans les sections qui suivent.

Retenons que la puissance active circule toujours de la source dont la tension est en avance vers la source dont la tension est en retard. L'amplitude de la tension n'affecte pas la direction de la puissance active.

Ainsi, dans la Fig. 25-23a, la puissance active circule de X vers Y parce que E₁ est en avance sur E₂. Par contre, si E₂ est en avance sur E₁ (Fig. 25-23d), la puissance active circule de Y vers X. (Notons que l'angle δ est négatif dans cette figure.)

 Cherchons maintenant une expression pour la puissance réactive associée à la source X.

Valeur de la puissance réactive

En se référant de nouveau aux Fig. 25-23a et 25-23b, on déduit de la manière suivante la puissance réactive Q débitée ou absorbée par la source X :

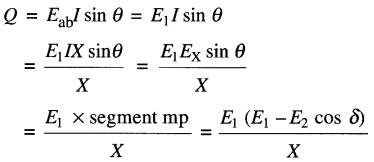
On peut donc écrire:

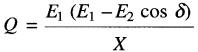    (25-14)

où

Q = puissance réactive débitée ou absorbée par la source X [var]
E₁ = tension efficace de la source X [V]
E₂ = tension efficace de la source Y [V]
δ = angle d'avance de Et sur E2
X = réactance reliant les sources X et Y [Ω]

Retenons que la source X débite de la puissance réactive lorsque Q est positive. Cette condition se produit lorsque E₁ est supérieure à la composante de tension E₂ cosδ.

Dans le cas contraire, la source X reçoit de la puissance réactive. Par exemple, dans la Fig. 25-23c où E₁ > E₂ cosδ, la source X débite de la puissance réactive.

Dans la section qui suit, en utilisant les formules 25-13 et 25-14, nous verrons comment l'angle δ et l'amplitude de E₂ permettent de commander les puissances P et Q.

Commande des puissances active et réactive

Supposons que l'on désire commander les puissances active et réactive débitées par une source X dont la tension E₁ est fixe.

 Connectons-la à travers une réactance X à une deuxième source Y dont la tension E₂ est variable en amplitude et en phase (Fig. 25-23a). Imposons de plus une contrainte au courant : le courant I ne doit pas dépasser une valeur nominale quelconque I_N. Par conséquent, la tension E_x aux bornes de la réactance ne doit pas dépasser XI_N.

Puissance active de la source X.

Supposons d'abord que l'on désire que X débite ou absorbe exclusivement une puissance active. Dans ces circonstances, il faut que le courant I soit en phase, ou déphasé de 180° avec la tension E₁.

Figure 25-24 Commande de la puissance active P_A

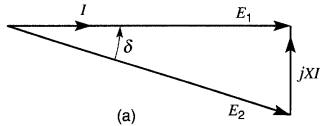
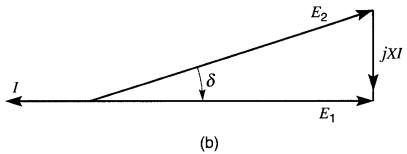
Lorsque le courant est en phase avec E₁ (Fig. 25-24a), l'angle S est positif; par conséquent P est positive car:

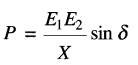    (25-13)

La source A débite alors une puissance active. Par contre, lorsque le courant est déphasé de 180° avec E₁ (Fig. 25-24b), l'angle S est négatif; par conséquent P est négative et X absorbe une puissance active. Dans un cas comme dans l'autre, Q est toujours égale à zéro.

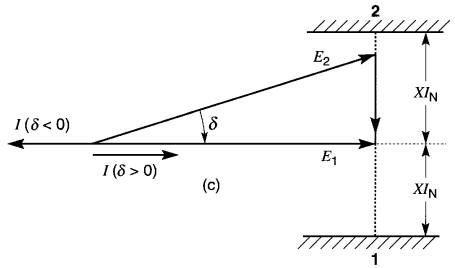
La Fig. 25-24c montre les deux diagrammes vectoriels combinés en un seul diagramme. On constate que lorsque l'on fait varier E₂, l'extrémité du vecteur E₂ suit le pointillé 1, 2 qui est perpendiculaire au vecteur E₁. En glissant le long de ce trait, le vecteur E₂ bute finalement contre les limites 1, 2 imposées par la chute de tension maximale XI_N au courant nominal I_N.

Donc, en faisant varier l'amplitude et la phase de la tension E₂ , on peut faire varier à volonté la puissance active débitée ou absorbée par la source X. Puissance réactive de la source X. Supposons maintenant que l'on désire que la source X débite ou absorbe exclusivement une puissance réactive.

Dans ces circonstances, il faut que le courant I soit 90° en retard, ou 90° en avance sur la tension E₁. De plus, en vertu de l'équation 25-13, une puissance active nulle impose un angle δ= 0.

Il faut donc que E₂ soit toujours en phase avec E₁ mais E₂ peut être inférieure ou supérieure à E₁.

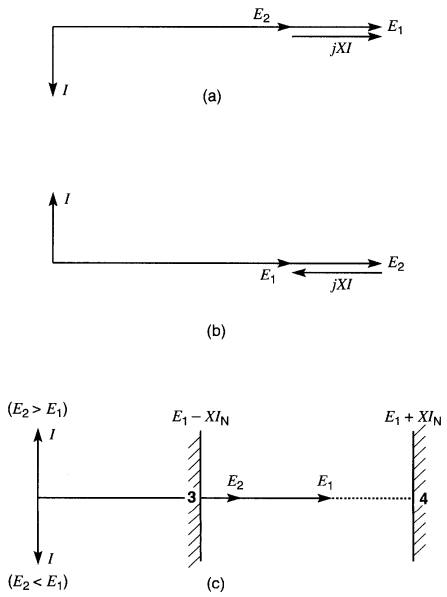
Lorsque E₂ < E₁ (Fig. 25-25a, Q est positive car d'après l'équation 25-14, on a:

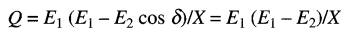
Dans ce cas, X débite une puissance réactive.

Par contre, lorsque E₂ > E₁ (Fig. 25-25b), Q est négative, ce qui signifie que la source X absorbe une puissance réactive. Ces deux possibilités sont combinées en un seul diagramme vectoriel (Fig. 25-25c). Dans cette figure, on constate que lorsque l'amplitude de E₂ varie, l'extrémité du vecteur E₂ suit le pointillé 3, 4.

En glissant le long de cette ligne, le vecteur E₂ atteint éventuellement les limites 3, 4 qui représentent les limites de chute de tension XI_N imposées par le courant nominal I_N.

Ces limites correspondent respectivement aux tensions

E₂ = E₁ - XI_N et E₂ = Et + XI_N.

En gardant δ= 0 et en faisant varier l'amplitude de E₂ , on peut donc faire varier à volonté la puissance réactive Q débitée ou absorbée par la source X.

Regardons maintenant ces conclusions d'un autre point de vue. Lorsque la source X débite une puissance réactive. le courant est 90° en retard sur E₁ ; c'est comme si une inductance était branchée entre ses bornes a et b Fig. 25-23a).

Par contre, lorsque la source X absorbe une puissance réactive, le courant est 90° en avance sur E₁; c'est comme si un condensateur était branché entre les bornes a et b. On constate que ce jeu de tensions offre la possibilité de simuler un condensateur ou une inductance variable, en faisant simplement varier l'amplitude et la phase de la tension E₂.

On peut ainsi contrôler, à volonté, des puissances réactives de plusieurs mégavars.

Enfin, en modifiant l'amplitude et la phase de E₂ on peut obtenir différentes combinaisons de P et de Q. Il suffit de limiter les tensions et les courants aux valeurs nominales admissibles par les sources X et Y.

En ce qui concerne la source Y, la puissance active P qu'elle absorbe est égale à la puissance P débitée par la source X, car la réactance X n'absorbe aucune puissance active.

Cependant, la puissance réactive absorbée par Y est égale à (Q -XI²). Lorsque cette expression est positive, cela indique que la source Y absorbe une puissance réactive.

Dans ce qui précède, nous avons utilisé une réactance X pour relier les sources X et Y. On aurait pu aussi contrôler les puissances P et Q de la même manière en utilisant une résistance. Cependant une résistance a l'inconvénient de chauffer et de consommer de l'énergie. Évidemment, l'utilisation d'une résistance au lieu d'une réactance changerait les formules ainsi que les diagrammes vectoriels.

Exemple 25-8

Une source A de 24 kV, 60 Hz, est raccordée à une source B de 25 kV par une réactance X de 3Ω (Fig. 25-26).

Figure 25-26 Voir exemple 25-8

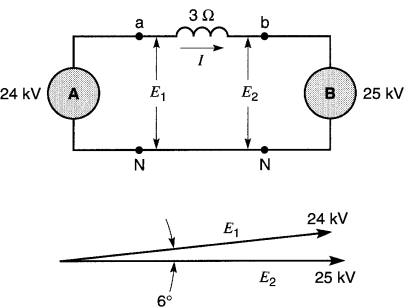
La tension E₁ est 6" en avance sur E₂ donc δ= 6°.

Calculer la valeur et la direction des puissances P_A, Q_A, P_B et Q_B.

Solution

La puissance active P_A est:

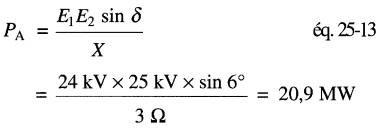
Étant donné que E₁ est en avance sur E₂, il s'ensuit que A débite cette puissance active.

Comme la réactance X n'absorbe aucune puissance active, la puissance absorbée par B est égale à P_A.

La puissance réactive associée à A est :

Puisque Q_A est négative, la source A reçoit cette puissance réactive comme si un condensateur était branché à ses bornes.

La puissance apparente de A est:

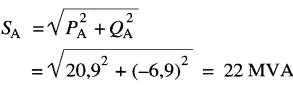
Le courant est donc:

I = 22 MVA / 24 kV = 917A

Il est évident que ce même courant circule dans la réactance et dans la source B.

La puissance réactive absorbée par la réactance est :

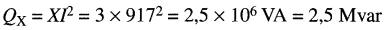
On obtient donc pour la source B :

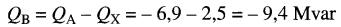
La puissance réactive Q_B étant négative, il s'ensuit que B débite de la puissance réactive. C'est logique, car comme la source A et la réactance X absorbent toutes deux de la puissance réactive, la source B doit nécessairement en débiter.

CALCUL VECTORIEL

Puissances sous forme vectorielle

Nous avons déjà utilisé le calcul vectoriel pour résoudre les circuits (voir section Diagrammes vectoriels). Nous l'appliquons maintenant au calcul des puissances active, réactive et apparente. Sur la Fig. 25-27a, le circuit branché entre les bornes a et b peut être plus ou moins complexe.

Figure 25-27 La direction du courant I et l'identification des bornes déterminent la direction des puissances P et Q obtenues par calcul vectoriel

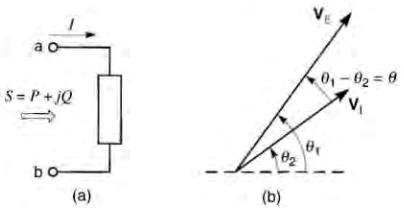
Ce circuit peut contenir des résistances, des réactances, des sources, ou toute combinaison de ces trois types d'éléments. Un courant I circule de la borne a vers la borne b. Supposons que la tension aux bornes du circuit soit exprimée par le vecteur V_E:

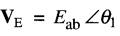
et que le courant soit représenté par le vecteur V_I :

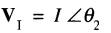
On sait que, par définition, le conjugué de V_I est un nouveau vecteur:

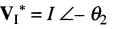
Par définition, le vecteur représentant la puissance apparente V_s associée* au circuit est:

* Le terme «associé» signifie la puissance active ou réactive qui est absorbée ou débitée par un circuit.

V_S = V_E V_I    (25-8)

soit :

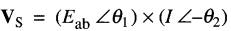
d'où:

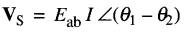
En remplaçant (θ₁ - θ₂) par θ, on peut écrire:

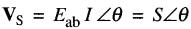    (25-9)

où

Vs = vecteur de la puissance apparente
S = valeur de la puissance apparente [VA]
θ = (θ₁ - θ₂) = déphasage de la tension par rapport au courant (si la tension est en avance  sur le courant, θ est positif)
E_ab = valeur efficace de la tension [V]
I = valeur efficace du courant [A]

L'expression polaire (25-9) peut aussi être mise sous la forme rectangulaire, soit :

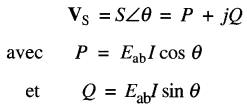    (25-10)

ou

P = puissance active associée au circuit [W]
Q = puissance réactive associée au circuit [var]
E_ab, I, θ  = grandeurs déjà définies dans la formule (25-9)

Il est important de retenir que les équations (25-8), (25-9), (25-10) sont basées sur la Fig. 25-27, soit sur une tension E_ab et un courant I qui circule de la borne a vers la borne b. Dans ce cas, les règles suivantes s'appliquent:

RÈGLES DES PUISSANCES

1. Si la valeur de P est positive, le circuit est une charge qui absorbe P watts

2. Si la valeur de P est négative, le circuit est une source qui débite P watts

3. Si la valeur de Q est positive, le circuit est une charge réactive qui absorbe Q vars

4. Si la valeur de Q est négative, le circuit est une source réactive qui débite Q vars

Exemple 25-9

Dans le circuit de la lia 2_5-28 où le courant circule dans le sens indiqué, on donne :

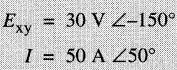
Déterminer la valeur des puissances active et réactive, et spécifier si les élément, A et B sont des sources ou des charges.

 Solution

Dans un circuit comprenant deux ou plusieurs éléments, on doit considérer chaque élément individuellement. Choisissons l'élément B.

On doit alors choisir une tension telle que ses indices soient conformes au sens de la circulation du courant I dans l'élément B.

Puisque le courant circule de la borne y à la borne x, on doit utiliser la tension E_yx (et non pas E_xy).

On a donc:

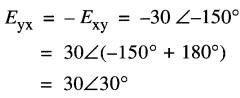
d'où

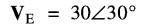
de plus, on a:

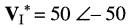
La puissance apparente associée à l'élément B est donc :

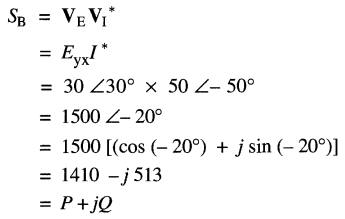
Puisque P = +1410 W, B est une charge, qui absorbe 1410 W (règle 1).

Puisque Q = -513 var, B est aussi une source réactive débitant 513 var (règle 4).

Connaissant les puissances associées à l'élément B, on peut immédiatement déduire celles associées à l'élément A: ce dernier est une charge réactive absorbant 513 var, en même temps qu'il est une source active débitant 1410 W.

Exemple 25-10

Dans le montage de la Fi , 25-26

Figure 25-29 Voir exemple 25-10

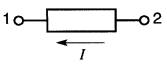
on donne:

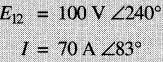
Déterminer la nature dies puissances active et réactive associées à ce montage.

Solution

Le courant circule de la borne 2 à la borne 1. On doit donc utiliser la tension E₂₁, (et non pas E₁₂) dans le calcul des puissances. La puissance apparente associée à l'élément est :

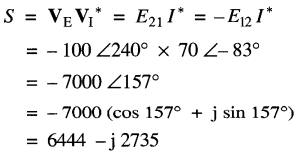
Donc le montage absorbe 6444 W et débite 2735 var.

Sens arbitraires des courants: effet sur les diagrammes vectoriels

Lors de l'étude à la section Circuits simples à courant alternatif nous avons appris que le courant dans une résistance est en phase avec la tension à ses bornes.

De plus, le courant dans une bobine est 90° en retard sur la tension, tandis que celui dans un condensateur est 90° en avance.

Cependant, dans la section Solutions des circuits à courant alternatif et la présente section, on a vu que l'on peut assigner des directions arbitraires aux courants dans un circuit. Ces choix arbitraires affectent l'apparence des diagrammes vectoriels sans pour autant affecter la solution du circuit.

Dans cette section nous démontrerons l'effet du changement de direction arbitraire d'un courant. Certains choix produisent des relations vectorielles inattendues bien qu'elles soient parfaitement correctes. Par exemple, on pourrait trouver que le courant dans une résistance est déphasé de 180° avec la tension à ses bornes.

Toutefois, on peut être confiant que lorsque les équations de Kirchhoff sont bien formulées, la résolution des courants, des tensions et des puissances apparentes donnera toujours la réponse juste. Les exemples suivants illustrent la méthodologie vectorielle pour trois montages simples.

Exemple 25-11

Une tension

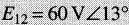
 est appliquée aux bornes d'une résistance de 4Ω (Fig. 25-30a).

Calculer:

a) le courant circulant dans le circuit

b) la puissance apparente associée à la source

Solution

a) Choisissons un courant I circulant arbitrairement de la borne 1 vers la borne 2 dans la résistance (Fig. 25-30b).

Figure 25-30 Voir exemple 25-11

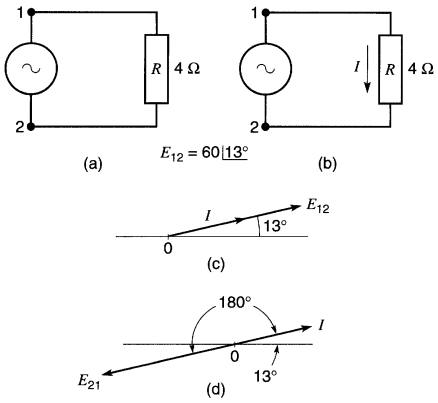
Écrivons l'équation de Kirchhoff en parcourant le circuit dans le sens horaire :

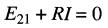
d'où

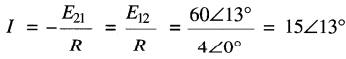
Le diagramme vectoriel est montré à la Fig 25-30e. On constate que le courant est en phase avec la tension, ce qui correspond à nos attentes pour un circuit résistif.

Toutefois, on peut mettre en évidence le vecteur E₂₁ au lieu du vecteur E₁₂, ce qui donne le diagramme vectoriel de la Fig. 25-30d. Dans ce cas, le courant dans la résistance est déphasé de 180° avec la tension à ses bornes. Ce diagramme vectoriel est tout aussi valable que celui de la Fig. 25-29e.

b) La puissance apparente associée à la source est donnée par S =E₂₁I*. (On prend la tension E₂₁ car dans la source le courant circule de la borne 2 à la borne 1.)

Comme

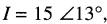
il s'ensuit que

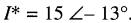
On peut donc écrire: 

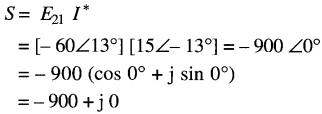
La puissance active associée à la source est de -900 W. Le signe négatif indique qu'elle débite en fait une puissance active de 900 W. La puissance réactive (j0) associée à la source est nulle.

Exemple 25-12

Une tension

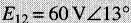
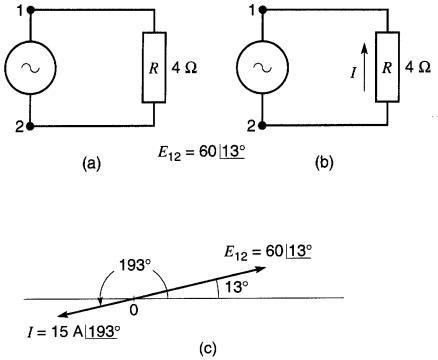
est appliquée aux bornes d'une résistance de 4Ω (Fig. 25-31 a).

Figure 25-31 Voir exemple 25-12

Calculer:

a) le courant dans le circuit

b) la puissance apparente associée à la source

Solution

a) Choisissons un courant I circulant arbitrairement de la borne 2 vers la borne 1 dans la résistance (Fig. 25-31b), soit l'inverse de celui de la Fig. 25-30b.

Écrivons l'équation de Kirchhoff en parcourant le circuit dans le sens horaire:

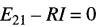
d'où

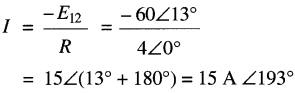
Le diagramme vectoriel est montré à la Fig 25-31c. On constate que le courant est déphasé de 180° avec la tension E₁₂. Bien que ce résultat puisse paraître bizarre, il est strictement correct.

Le diagramme vectoriel de la Fig. 25-31c (qui découle du schéma de la Fig. 25-31b) est aussi valable que celui de la Fig. 25-30c.

b) La puissance apparente associée à la source est donnée par S = E₁₂1*. (On prend la tension E₁₂ car dans la source le courant circule de la borne 1 à la borne 2.)

Comme

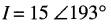
il s'ensuit que

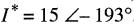
On peut donc écrire:

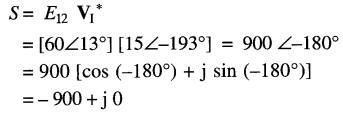
La puissance active associée à la source est de -900 W, ce qui indique qu'elle débite en fait une puissance active de 900 W. La puissance réactive (j0) est nulle. On constate que le fait d'avoir changé le sens du courant n'a aucunement affecté les puissances active et réactive associées à la source.

Résumé

Dans cette section nous avons vu que tous les composants d'un circuit ou réseau électrique à courant alternatif peuvent se comporter comme une source ou une charge, active ou réactive.

Nous avons appris comment connecter un wattmètre et un varmètre pour mesurer respectivement la puissance active et la puissance réactive.

Le facteur de puissance d'un circuit est un nombre inférieur ou égal à 1 définissant le rapport entre la puissance active et la puissance apparente.

On a vu qu'un condensateur, qui est une source de puissance réactive, permet d'améliorer le facteur de puissance, et donc de réduire le courant d'un circuit qui consomme de la puissance réactive (ex. : circuit inductif, moteur).

On a vu qu'il est possible de résoudre un circuit en faisant simplement le bilan des puissances active et réactive. Cette méthode permet de résoudre des circuits à c.a. sans faire appel au calcul vectoriel. Nous avons aussi donné les formules permettant de calculer les circulations de puissance active et réactive entre deux sources reliées par une réactance inductive.

On a constaté qu'il est possible de simuler un condensateur ou une inductance simplement en agissant sur l'amplitude et la phase de l'une des deux sources.

Enfin, on a vu comment utiliser le calcul vectoriel pour calculer les puissances à partir des vecteurs de tension et de courant. La puissance apparente est elle-même un vecteur qui, exprimé sous forme rectangulaire, donne la puissance active et réactive.

PROBLÈMES

Niveau pratique

25-1 Nommer l'unité de puissance active ; de puissance réactive; de puissance apparente.

25-2 Un condensateur de 500 kvar est mis en parallèle avec une inductance de 400 kvar. Quelle est la puissance apparente de l'ensemble?

25-3 Nommer un dispositif statique qui génère une puissance réactive.

25-4 Nommer un dispositif statique qui absorbe une puissance réactive.

25-5 Quel est le facteur de puissance d'un condensateur? d'une bobine? d'une lampe à incandescence?

Niveau intermédiaire

25-6 Une ligne alimente les charges suivantes :

1) une résistance de 120 kW

2) une bobine de 40 kvar

3) un condensateur de 90 kvar

Calculer la puissance apparente de l'ensemble de ces charges, ainsi que le facteur de puissance.

25-7 Un moteur d'induction absorbe une puissance apparente de 400 kVA à un facteur de puissance de 80%.

a) Calculer la puissance active absorbée par la machine.

b) Quelle est la puissance réactive et à quoi sert-elle?

25-8 Dans la Fig. 24-3 (chapitre 24),

calculer:

a) la puissance active absorbée par la résistance

b) la puissance réactive absorbée par l'inductance

c) la puissance apparente de l'ensemble

d) le facteur de puissance de l'ensemble

25-9 Dans la Fig. 24-17,

calculer:

a) la puissance réactive absorbée par la bobine

b) la puissance réactive générée par le condensateur

c) la puissance active dissipée par la bobine

d) la puissance apparente de l'ensemble e) le facteur de puissance de l'ensemble

25-10 Dans la Fig. 24-16,

calculer:

a) la puissance réactive totale de la charge

b) le FP de l'ensemble

25-11 Une bobine, ayant une résistance de 5Ω, porte un courant continu de 20A.

a) Quelle est la puissance active absorbée?

b) Quelle est la puissance réactive absorbée?

25-12 Dans la Fig. 25-16, on branche une réactance inductive de 19Ω en parallèle avec la source de 380V.

Calculer:

a) la puissance réactive de l'ensemble

b) la puissance apparente de l'ensemble

c) le facteur de puissance de l'ensemble

Niveau avancé

25-13 Un moteur ayant un facteur de puissance de 80 % absorbe une puissance active de 1200 W.

Calculer la puissance réactive absorbée.

25-14 Dans la Fig. 25-14, on branche un condensateur de 30 kvar en parallèle avec le moteur.

Calculer:

a) la puissance active absorbée par l'ensemble

b) la puissance apparente absorbée par l'ensemble

c) le FP de la source

25-15 Dans la Fig. 25-19, calculer la valeur, en ohms. de la réactance inductive qu'il faudrait placer en parallèle avec la résistance afin que le facteur de puissance de l'ensemble devienne 100 %.

25-16 Une source monophasée de 240 V alimente une charge de 160 kW ayant un FP de 80 %.

Calculer le courant dans la ligne.

25-17 Dans la Fig. 25-15, on remplace le condensateur de 45 kvar par un autre de 35 kvar.

Calculer:

a) la puissance réactive fournie par la source

b) la puissance active fournie par la source

c) le courant fourni par la source

25-18 Une ligne monophasée relie un poste de transformation à une charge. Les instruments indiquent les valeurs suivantes:

au poste:

P_t = 36 MW, S_t = 39 MVA, tension = 115 kV

à la charge:

P₂ = 35 MW S₂ = 37 MVA

Calculer:

a) le courant dans la ligne

b) la tension à la charge

c) la résistance et la réactance inductive de la ligne

d) l'angle de déphasage entre la tension au poste et la tension à la charge

25-19 En se référant à la Fig. 24-25b (section Solutions des circuits à courant alternatif).

calculer l'impédance du circuit vue entre les bornes 1 et 2. Utiliser la méthode des puissance et supposer une tension de 72V aux bornes du condensateur de 72Ω. Dès lors, déterminer l'angle entre la tension E et le courant I₁.

25-20 En se référant à la Fig. 25-32, calculer la valeur des puissances active, réactive et apparente associées à l'impédance Z.

Utiliser le calcul vectoriel décrit dans la section 25-14.

Figure 25-32 Voir problème 25-20

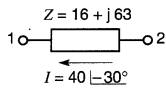
25-21 En se référant à la Fig. 25-33

Figure 25-33 Voir problème 25-21

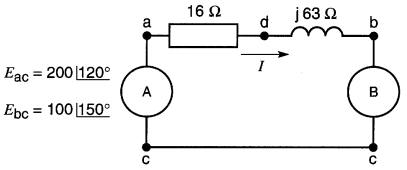
et en utilisant le calcul vectoriel, déterminer:

a) les puissances active et réactive associées à la source A

b) les puissances active et réactive associées à la source B

c) la puissance active dissipée dans la résistance de 16Ω

d) la puissance réactive absorbée par la réactance de 63Ω

e) Faire le bilan des puissances actives pour le circuit et vérifier que le tout s'équilibre.

f) Faire le bilan des puissances réactives pour le circuit et vérifier que le tout s'équilibre.

25-22 Une tension

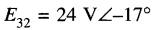
apparaît aux bornes d'une réactance inductive de 3Ω (Fig. 25-34).

Figure 25-34 Voir problème 25-22

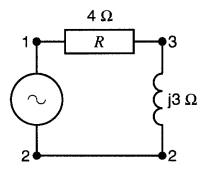
On désire connaître:

a) la valeur du courant dans le circuit

b) la valeur de la tension E₁₂

c) la puissance associée à la source Choisir un sens de courant I circulant arbitrairement de la borne 2 vers la borne 3 dans la réactance.

Réponses

2)100 kvar capacitif; 5) 0%; 0%; 100%; 6)130 kVA; 92,3% en avant;
7a) 320 kW; 7b) 240 kvar; 8a) 1200 W; 8b) 500 var; 8c) 1300 VA;
8d) 92,3% arrière; 9a) 3842 var; 9b) 5000 var; 9c) 768 W;
9d) 1388 VA; 9e) 55,3% avant; 10a) 0; 10b) 100%; 11 a) 2 kW;
11b) 0; 12a) 12,6 kvar; 12b) 27,1 kVA; 12c) 88,6%; 13) 900 var;
14a) 28 kW; 14b) 31,8 kVA; 14c) 88,2% arrière; 15) 51,4Ω;
16) 833 A; 17a) 10 kvar; 17b) 28 kW; 17c) 70,1 A; 18a) 339 A;
18b) 109,1 kV; 18c) 8,7 + j 26,1 ; 18d) Eposte est 3,7° en avance sur
Echarge; 19) Z = 35,6Ω; I est 24,9° en arrière de E;
20) 25,6 kW; 100,8 kvar; 104 kVA; 21 a) A: absorbe 62,7 W
et génère 374,8 var; 21 b) B : génère 120,9 W et absorbe 146,6 var;
21c) 57,8 W; 21d) 227,4 var