Phénomènes électrostatiques
Nous avons tous eu la désagréable sensation de prendre un choc en touchant une poignée de porte ou un autre objet métallique après avoir marché sur un tapis. Ce choc correspond à une décharge électrique momentanée entre le corps humain et l'objet touché.
Ce phénomène s'explique par cette science qu'on appelle électrostatique. L'électrostatique est l'étude des charges positives et négatives qui sont prisonnières à un endroit ou sur un objet quelconque.
Le coulomb - unité de quantité d'électricité
La plus petite quantité d'électricité ou charge électrique connue est celle portée par un électron. Cependant, elle est si infime qu'on préfère utiliser le coulomb, unité SI de quantité d'électricité correspondant à la charge de 6,2 x 1018 électrons. Le coulomb (symbole C) est la quantité d'électricité transportée en 1 seconde par un courant de 1 ampère.
Électrons libres dans un métal
On a vu à la section Nature de l'électricité qu'une quantité inouïe d'électrons libres fourmille à l'intérieur d'un conducteur. On estime que dans la plupart des métaux leur nombre correspond à environ 1010 coulombs par mètre cube.
Une mince plaque de cuivre ayant une surface de 1 cm² et une épaisseur de 1 mm contient donc une charge de 1000 coulombs d'électrons libres. Ces électrons se déplacent au hasard à une vitesse moyenne d'environ 1000 km/s.
Cette charge négative mobile est annulée par la charge positive équivalente située sur les noyaux fixes des atomes. Les électrons sont «libres» en ce sens qu'ils ne sont pas attachés à un atome en particulier, mais sont tous prisonniers à l'intérieur du morceau de métal et ne peuvent lui échapper malgré leur grande vitesse.
Les parois du métal constituent des «murs» qui empêchent les électrons de sortir.
Par ailleurs, si un électron venant de l'extérieur touche le morceau métallique, il est aussitôt capté par celui-ci, devenant à son tour prisonnier à l'intérieur des «murs».
Transfert de charges et d.d.p.
Considérons deux corps métalliques parfaitement isolés l'un de l'autre et initialement neutres (Fig. 20-1).
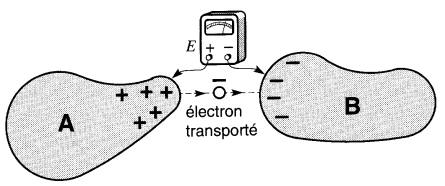
Figure 20-1 Le transport d'une charge électrique d'un corps à un autre produit une différence de potentiel que l'on peut mesurer au moyen d'un voltmètre
L'isolant qui les sépare peut être de l'air, un isolant liquide ou solide, ou le vide. Admettons que, par un moyen quelconque, on soit capable d'enlever des électrons libres du corps A et de les déposer sur le corps B.
Il en résulte un manque d'électrons sur le corps A, ce qui lui donne une charge positive, alors que le surplus d'électrons accumulés sur le corps B lui donne une charge négative. Cette différence de charge électrique entre les deux corps donne naissance à une différence de potentiel (abréviation d.d.p.).
Si l'on raccorde un voltmètre entre les deux corps, on constate bien qu'une tension électrique existe entre eux (Fig. 20-1).
Plus on transfère d'électrons du bloc A au bloc B, plus cette tension augmente. Des expériences ont démontré que la tension entre deux corps est proportionnelle au nombre d'électrons transférés, ou encore au nombre de coulombs transférés. La différence de potentiel dépend aussi des dimensions et de la forme des corps, de la distance qui les sépare et de la nature du milieu isolant.
Même s'il y a un grand nombre d'électrons libres à l'intérieur d'un corps métallique, il suffit d'en transporter une fraction infime pour produire des tensions très élevées.
Par exemple, si l'on transfère seulement 1 nanocoulomb entre deux plaques ayant une superficie de 1 cm2 et séparées par une épaisseur d'air de 1 centimètre, il en résulte une différence de potentiel d'environ 10 000 volts (Fig. 20-2a et 20-2b).
Figure 20-2a Chaque plaque métallique contient des électrons libres dont la charge totale équivaut à 1000 coulombs
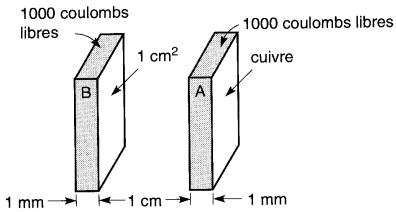
Figure 20-2b Si l'on transporte seulement 10-9 coulombs de la plaque A à la plaque B, il en résulte un d.d.p. de 10 kV
Forces et énergie électrostatiques
Le fait de transporter une charge électrique d'un corps à un autre non seulement produit une différence de potentiel, mais crée aussi des forces, une transformation de l'énergie mécanique en énergie électrostatique et un champ électrique.
Ainsi, lorsqu'on transporte un électron d'un corps positif à un corps négatif, il faut exercer une force car l'électron est à la fois repoussé par le corps négatif et attiré par le corps positif.
On doit donc dépenser de l'énergie pour transporter une charge d'un corps à un autre. Qu'arrive-t-il de cette énergie?
Elle est emmagasinée dans le diélectrique (isolant) séparant les deux corps sous forme d'énergie électrostatique.
Sa valeur est donnée par l'expression:
W = 1/2 (Q/E)
où
W = énergie
électrostatique, en joules [J]
Q = charge transportée, en coulombs [C]
E =
tension entre les deux corps, en volts [V]
Il est utile d'imaginer que l'espace séparant les deux corps chargés est rempli d'un champ électrique. L' énergie électrostatique est emmagasinée dans ce champ électrique de la même façon que l'énergie magnétique est conservée dans le champ magnétique d'un entrefer.
Décharge des corps
Si l'on réunit les deux corps de la Fig. 20-1 par un fil conducteur, les électrons en surplus sur le corps négatif s'enfuient vers le corps positif, provoquant un courant intense dans le fil pendant un instant seulement. La même chose se produit si on réunit les deux plaques de la Fig. 20-2b.
Au moment du contact une étincelle jaillit et provoque un dégagement de chaleur. Cette chaleur dissipée provient de l'énergie électrostatique emmagasinée qui diminue rapidement jusqu'à zéro pendant la décharge. Dès que les charges sont équilibrées, le courant cesse et le champ électrique disparaît.
Conversion de l'énergie mécanique en énergie électrostatique
Les deux corps de la Fig. 20-3a portent des charges opposées de sorte qu'ils s'attirent avec une certaine force.
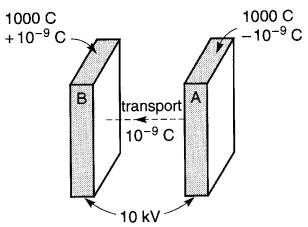
Figure 20-3 Conversion d'énergie mécanique en énergie électrostatique :
a. De l'énergie est emmagasinée dans le champ électrostatique.
b. En séparant les corps, le travail mécanique se transforme directement en énergie électrostatique
Il s'ensuit que pour les éloigner, il faut dépenser un travail mécanique que l'on peut exprimer en newton mètres.
Qu'arrive-t-il de cette énergie mécanique?
Elle sert à augmenter l'énergie électrostatique emmagasinée entre les deux corps.
L'énergie électrostatique est donc plus grande dans la Fig. 20-3b que dans la Fig. 20-3a, la différence étant exactement égale au travail mécanique effectué en séparant les corps.
Tout comme l'énergie mécanique est convertie directement en énergie magnétique quand on éloigne les pôles d'un aimant (section Hystérésis et aimants permanents, l'énergie mécanique est convertie directement en énergie électrostatique lorsqu'on augmente la distance entre deux corps chargés.
Augmentation de la tension
L'augmentation de la distance entre deux corps chargés est accompagnée d'une croissance de la tension entre les corps.
Ce phénomène surprenant s'explique d'après la formule (20-1); en effet, puisque la charge Q demeure la même, l'énergie électrostatique ne peut augmenter que si la tension entre les deux corps augmente à mesure qu'on les éloigne.
L'augmentation de la tension est particulièrement remarquable lorsque l'on sépare deux plaques initialement très rapprochées comme celles montrées à la Fig. 20-4a.
Figure 20-4
a. Les plaques sont très rapprochées et la tension entre elles est seulement de 10V
b. En augmentant la distance à 1 mm, la tension monte à 1000V
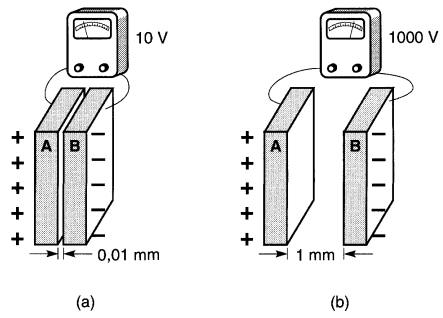
Si l'on augmente la distance de 0,01 mm à 1 mm, la tension initiale de 10V augmente d'environ 100 fois, atteignant une valeur de 1000V après la séparation (Fig. 20-4b). Cette augmentation de la tension avec la distance servira à expliquer plusieurs phénomènes électrostatiques.
Transfert de charges par contact mécanique
En pratique, tous les matériaux, les isolants aussi bien que les conducteurs, possèdent une quantité plus ou moins grande d'électrons libres. Théoriquement, si l'on pouvait les saisir, on pourrait enlever ces électrons d'un corps et les déposer sur un autre, comme on vient de l'imaginer.
Il existe cependant deux méthodes plus pratiques pour effectuer le transfert : le transfert par simple contact mécanique et le transfert à l'aide d'une source de tension.
Lorsque deux matériaux différents, mais électriquement neutres, se touchent, il se produit en général un transfert d'électrons de l'un à l'autre. Le nombre d'électrons transférés dépend des matériaux, quelques-uns étant plus susceptibles d'effectuer un échange important que d'autres.
Ainsi, lorsqu'un morceau de soie vient en contact avec un morceau de verre, ce dernier devient positif, ayant cédé quelques électrons au morceau de soie (Fig. 20-5).
Figure 20-5 Un transfert de charge se produit en frottant le verre avec un morceau de soie; la soie accapare des électrons alors que le verre en perd
Le frottement n'est pas nécessaire pour que ce transfert d'électrons se produise, le simple contact suffit; mais comme le frottement produit un contact plus intime, il facilite le transfert des charges.
Le même phénomène se produit quand on marche sur un tapis par temps sec. Le contact répété entre la semelle du soulier et la surface du tapis produit un transfert de charges qui augmente à chaque pas, de sorte que le corps humain devient très positif par rapport à ses environs.
Cette charge accumulée est suivie d'une décharge violente lorsqu'on touche une poignée de porte. Le transfert d'électrons peut se faire lorsque des conducteurs ou des isolants se touchent.
Ainsi, le contact momentané entre les cristaux de glace et les gouttes d'eau en suspension dans un nuage produit une séparation des charges qui donne éventuellement naissance à des éclairs.
Le contact du blé ou de la farine avec le tuyau métallique qui les transporte peut également produire des transferts de charges importants, ce qui peut parfois provoquer une décharge électrique dangereuse.
Lorsque deux matériaux différents se touchent, le transfert d'électrons produit, au maximum, une différence de potentiel de quelques volts.
Cependant, lorsque les deux matériaux sont séparés, la tension augmente de plusieurs milliers de fois, de sorte que l'on peut observer des étincelles dans certains cas. C'est à ce phénomène qu'on attribue les décharges électrostatiques créées par des courroies en contact avec des poulies métalliques, par le passage d'un peigne dans les cheveux, etc.
Transfert de charges à l'aide d'une source de tension
La méthode la plus simple pour transférer des électrons d'un corps à un autre consiste à relier deux plaques métalliques à une batterie de piles (Fig. 20-6a).
Figure 20-6a Transfert d'une charge électrique au moyen d'un accumulateur
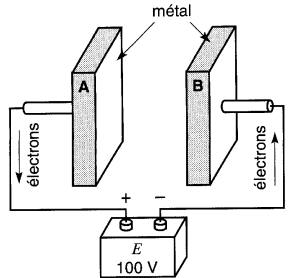
Des électrons sont aussitôt enlevés de la plaque reliée à la borne (+) de la batterie et déposés sur la plaque reliée à la borne (-), de sorte que la tension entre les plaques augmente rapidement.
Dès que cette tension atteint la tension E de la source, le courant cesse. On peut alors débrancher la batterie, et la tension E subsistera indéfiniment entre les deux plaques (Fig. 20-6b).
Figure 20-6b La tension entre les plaques est égale à celle de l'accumulateur
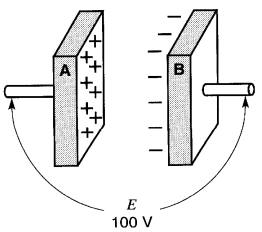
De la même façon, on peut transporter des charges entre deux corps isolants (Fig. 20-7a et 20-7b). Cependant, les électrons ainsi transférés tendent à être soutirés autour de la région X et déposés autour de la région Y.
Figure 20-7a Transfert d'une charge électrique entre deux isolants
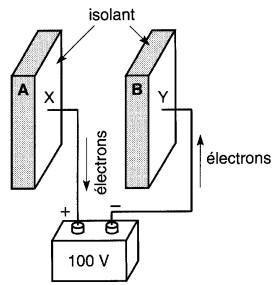
Figure 20-7b Les charges sur un isolant tendent à demeurer en place
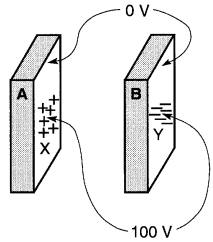
En effet, ils ne sont pas libres de se répandre dans le corps isolant tout entier comme ils peuvent le faire dans le cas d'un conducteur. Un voltmètre raccordé aux régions X(+) et Y(-)indique une tension, alors qu'il n'indique rien s'il est raccordé en dehors de ces régions.
En d'autres termes, les charges déposées sur un isolant tendent à demeurer en place.
Distribution des charges sur deux sphères conductrices
Considérons deux sphères métalliques A et B assez rapprochées, entre lesquelles on a transporté une certaine charge de sorte que A soit positive et B négative (Fig. 20-8a).
Figure 20-8a Distribution non uniforme des charges sur deux sphères conductrices voisines
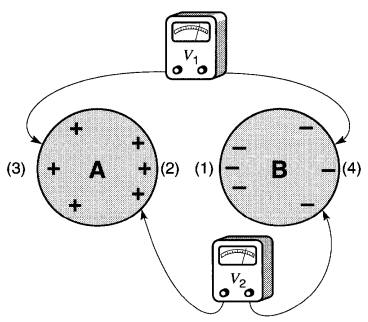
Les électrons en surplus sur la sphère B se repoussent mutuellement et tendent à se répartir uniformément sur toute sa surface. Cependant, comme ils sont attirés par la charge positive de la sphère A, la concentration des électrons est plus grande sur le côté (1) en regard de la sphère A.
De même, cette concentration d'électrons sur la sphère B repousse les électrons libres de la sphère A de sorte que ces derniers sont obligés de se distribuer sur la face opposée (3).
Il s'ensuit que la charge positive est moins concentrée sur la face (3) que sur la face (2).
La charge positive sur A et la charge négative sur B ne sont donc pas réparties de façon uniforme. Cependant, la différence de potentiel entre deux points quelconques de la même sphère est rigoureusement nulle.
En effet, comme il s'agit d'un conducteur, s'il existait la moindre différence de potentiel entre deux points quelconques de la sphère, les électrons se déplaceraient aussitôt pour l'annuler.
Plus généralement, tous les points d'un corps conducteur sont donc au même potentiel peu importe la distribution des charges.
Il s'ensuit que la tension entre un point de la sphère A et un point quelconque de la sphère B reste la même. Le voltmètre V1 lira donc la même tension que le voltmètre V2.
Si maintenant on éloigne les sphères d'une grande distance afin que leurs charges respectives ne s'influencent plus, les charges se répartiront uniformément autour des surfaces A et B (Fig. 20-8b).
Figure 20-8b En éloignant les sphères, les charges se répartissent uniformément autour de leur surface
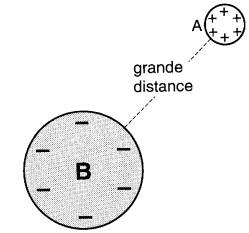
Évidemment, le fait de déplacer les sphères augmente la tension entre elles, mais ne change pas les charges positives et négatives qu'elles portent.
Champ et lignes de force électriques
On avait déjà mentionné ci-haut qu'il est utile d'imaginer que l'espace séparant deux corps chargés renferme un champ électrique.
Tout comme le champ magnétique est composé de lignes de force magnétiques, ce champ électrique est composé de lignes de force électriques. Ces lignes n'existent pas en réalité mais elles aident à comprendre les phénomènes électrostatiques; de plus elles permettent de déterminer les spectres du champ électrique.
Il suffit d'appliquer les règles suivantes:
1. Les lignes partent toujours d'une charge positive et aboutissent sur une charge négative de même valeur. La grandeur de cette charge est arbitraire, mais pour un spectre donné, chacune des lignes doit réunir des charges de même valeur.
À la limite, on peut imaginer que chaque ligne aboutit sur un électron. Contrairement aux lignes de force magnétiques, les lignes de force électriques ne forment pas des boucles fermées mais elles réunissent des charges identiques de signes contraires.
Il existe toutefois une importante exception à cette règle: il s'agit du champ électrique entourant un champ magnétique qui varie. Dans ce cas, le champ électrique forme des boucles fermées (section Induction électromagnétique). La direction des lignes est indiquée par une flèche.
2. Les lignes de champ électriques sont semblables à des fils élastiques tendus entre lesquels existe une force de répulsion.
3. Les lignes ne se croisent jamais.
4. Les lignes tendent à suivre le chemin le plus court ou le plus facile.
5. Les lignes s'orientent toujours perpendiculairement à la surface d'un corps conducteur.
6. Des lignes réunissent toujours deux points entre lesquels existe une différence de potentiel.
Spectres électriques
La Fig. 20-9 montre le spectre du champ électrique pour quelques corps métalliques de formes différentes.
Figure 20-9 Divers spectres du champ électrique entre deux corps chargés
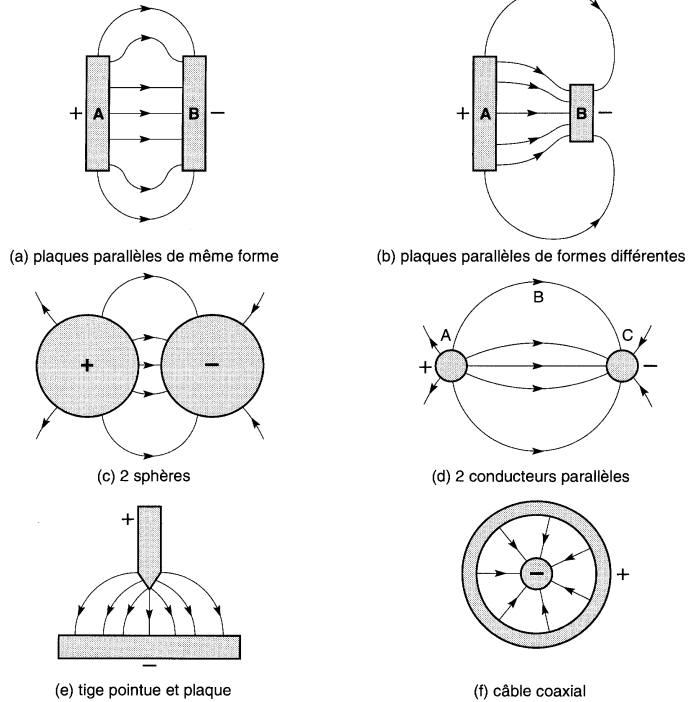
On a supposé que tous les corps portent le même nombre (sept) de charges, ce qui donne ainsi le même nombre de lignes pour chaque cas.
On observe que dans certaines régions entre les corps, les lignes sont plus concentrées ; à ces endroits, la force s'exerçant sur un électron (ou sur une charge quelconque) sera plus forte.
Pour une charge positive, la force agit toujours dans le sens de la flèche.
Par exemple, si l'on place une petite charge positive proche du point A (Fig. 20-9d), elle suivra la ligne ABC pour aboutir sur le conducteur (-). La force est intense aux points A et C mais faible au point B où les lignes sont moins concentrées.
De la même façon, la force est plus grande près de la pointe de la tige (Fig. 20-9e) que près de la plaque. On dit alors que le champ électrique est fort aux endroits où la force s'exerçant sur une charge libre est grande.
Le terme «champ électrique» possède deux significations:
(1) région entourant un corps chargé et emmagasinant de l'énergie et (2) quantité précise E dont l'unité est le volt par mètre.
Dans le SI, le champ électrique s'exprime en volts par mètre (V/m).
Par exemple, deux plaques planes ayant une différence de potentiel de 1000 V et séparées d'une distance de 0,01 m créent entre elles un champ électrique de 1000 V/0,01 m = 100 000 V/m.
La force s'exerçant sur une particule chargée placée dans un champ électrique est donnée par l'expression:
F = qE (20-2)
où
F = force sur la
particule, en newtons [N]
q = charge de la particule, en coulombs [C]
E =
champ électrique, en volts par mètre [V/m]
C'est par simple coïncidence que le symbole E utilisé pour une tension (volts) désigne aussi un champ électrique (volts par mètre).
Ionisation - applications et inconvénients
Si un gaz est traversé par un champ électrique suffisamment intense, la force agissant sur les électrons libres peut les accélérer pour déclencher l'ionisation du gaz.
On a déjà vu ce phénomène lors de l'étude des isolants (section Isolants) ; on sait que l'air s'ionise et devient conducteur lorsque l'intensité du champ électrique atteint 3 kV/mm (ou 3 MV/m). Ce phénomène d'ionisation trouve des applications importantes comme dans la précipitation électrostatique de la poussière, le dépôt électrostatique de la peinture et la reproduction par xérographie.
Ces procédés de mandent une ionisation contrôlée qu'on peut réaliser en donnant une forme appropriée aux électrodes sous tension. Supposons, par exemple, qu'on augmente la tension graduellement entre deux plaques métalliques parallèles.
L'intensité du champ électrique entre les plaques étant uniforme (Fig. 20-9a), lorsqu'elle atteint la valeur critique de 3 kV/mm l'air s'ionise partout et il se produit un arc qui court-circuite les plaques .
Par contre, si l'on applique une tension croissante en- tre un cylindre métallique et un conducteur central (Fig . 20-9f), le champ électrique E est plus élevé près du conducteur central que près du cylindre .
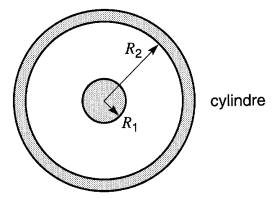
À la surface, ces champs sont dans le rapport des rayons respectifs R1 et R2 (Fig. 20-10).
Figure 20-10 Cylindre métallique ayant un rayon intérieur R2 et conducteur coaxial ayant un rayon R1
On peut donc écrire:
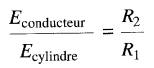(20-3)
Si ce rapport est de 10, l'ionisation débute autour du conducteur central dès que le champ électrique atteint 3 kV/mm, alors qu'il n'est que de 300 V/mm près du cylindre.
À mesure que la tension croît, l'épaisseur de la région ionisée autour du conducteur central augmente, sans toutefois provoquer un arc entre les deux électrodes (Fig. 20-11).
Figure 20-11 À mesure que l'on augmente la tension entre les deux électrodes, la région ionisée augmente
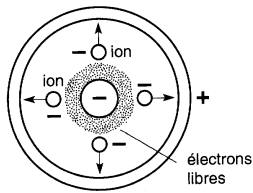
Si le conducteur central est négatif par rapport au cylindre, il crée un flot d'électrons libres dans la région ionisée.
Ceux-ci s'attachent aussitôt aux molécules d'air pour les transformer en ions négatifs. Par milliards, ces ions progressent lentement vers le cylindre positif où ils se débarrassent de leurs électrons parasites pour redevenir des molécules neutres.
La précipitation électrostatique utilise ce principe pour purifier les fumées d'usines et empêcher ainsi des mil- lions de tonnes de poussière de se répandre dans l'atmosphère.
Le système est composé d'un fil conducteur raccordé à une source de haute tension, entouré d'un cylindre métallique, ce dernier servant à la fois de cheminée pour les gaz poussiéreux et d'électrode (Fig. 20-12).
Figure 20-12 Épuration de la fumée
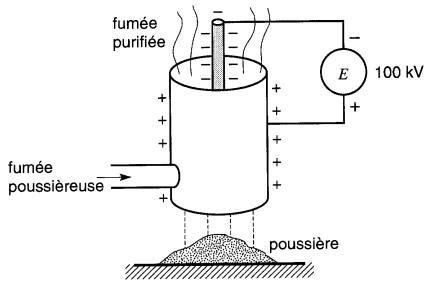
Les ions négatifs mentionnés précédemment s'attachent aux particules de poussière. La force électrostatique les amène vers le cylindre où elles perdent leur charge et, devenant des particules neutres, tombent dans des récipients appropriés (Fig. 20-13).
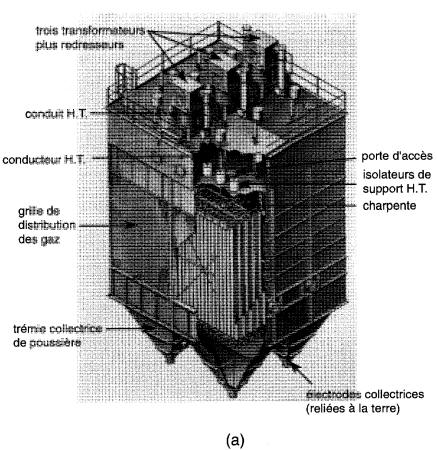
Figure 20-13
a. Vue en coupe d'un précipitateur industriel
b. Ce précipitateur purifie la fumée dégagée par une centrale thermique de génération d'électricité. Il élimine des dizaines de tonnes de poussière par heure
Il existe une relation entre le champ électrique à la sur- face du conducteur central et la tension appliquée entre le conducteur et le cylindre.
Elle est donnée par l'équation:
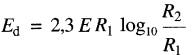(20-4)
où
Ed tension
continue appliquée entre le conducteur et le cylindre [V]
E = champ électrique à la
surface du conducteur central [V/m]
R1 = rayon extérieur du
conducteur central [m]
R2 = rayon intérieur
du cylindre [m]
2,3 = une constante
Exemple 20-1
Un conducteur n° 21 est situé au centre d'un cylindre ayant un rayon intérieur de 2 cm. Calculer la tension qu'on doit appliquer entre le conducteur et le cylindre, afin que l'air s'ionise autour du conducteur.
Solution
Un champ électrique E de 3 MV/m = 3 x 106 V/m provoquera l'ionisation de l'air.
Le conducteur n° 21 possède un diamètre de 0,72 mm, soit un rayon de 0,00036 m.
On obtient donc:
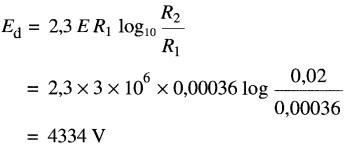
Le phénomène d'ionisation a parfois ses inconvénients. Par exemple, le champ électrique intense qui règne autour des conducteurs d'une ligne à haute tension pro- duit une ionisation qu'on appelle effet couronne.
Le soir, on peut parfois observer la lueur qui s'en dégage. L'effet couronne provoque des pertes le long des lignes de transport mais son effet le plus néfaste est l'interférence qu'il crée dans les postes de radio et de télévision. La décharge incessante produit de l'énergie radiante qui tend à brouiller la réception.
Afin de réduire l'effet couronne, il faut grossir les conducteurs à me- sure que la tension augmente. Par exemple, pour une ligne fonctionnant à 500 kV, les conducteurs doivent avoir un diamètre d'au moins 60 mm. Lorsque la tension est supérieure à 300 kV, on utilise souvent des conducteurs en faisceaux de 2, 3 ou 4 sous-conducteurs.
Cette construction donne l'équivalent d'un conducteur ayant un diamètre beaucoup plus grand que celui des sous-conducteurs.
Par exemple, sur les lignes à 735 kV reliant Montréal à Churchill Falls, on utilise un faisceau de 4 sous-conducteurs disposés sur un carré de 457 mm (Fig. 20-14a et 20-14b).
Figure 20-14a Ligne triphasée à 735 kV traversant la rivière Saguenay. Chacune des trois phases est composée de 4 conducteurs en parallèle lesquels sont retenus en place par des séparateurs métalliques. Le faisceau de 4 conducteurs forme un conducteur dont le diamètre effectif est de 441 mm (gracieuseté de Hydro-Québec).
Figure 20-14b Détail du faisceau de 4 conducteurs. En grossissant le diamètre effectif de chaque phase, on réduit les pertes par effet couronne. De plus, cela réduit l'inductance des lignes
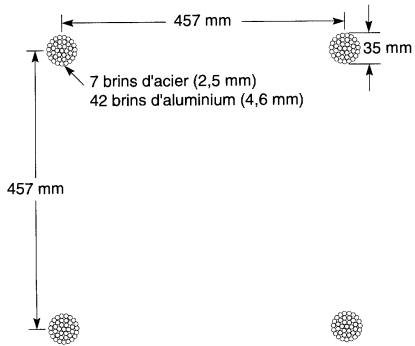
Du point de vue de l'effet couronne, cet arrangement équivaut à un conducteur rond ayant un diamètre de 441 mm.
Phénomènes atmosphériques
Par un procédé qui n'est pas entièrement compris, il se produit à l'intérieur de certains nuages une séparation des charges positives et négatives, les charges positives allant vers le haut du nuage alors que les charges négatives restent en bas (Fig. 20-15).
Figure 20-15 Champ électrique créé par un nuage lors d'un orage électrique
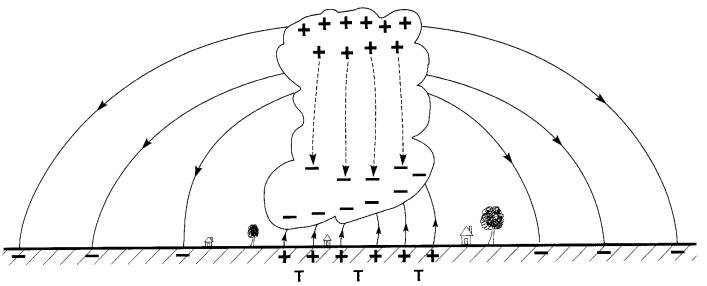
Il s'établit des lignes de champ électriques à l'intérieur du nuage entre les charges (+) et (-).
Cependant, la charge négative proche de la surface de la terre chasse les électrons libres de celle-ci, de sorte que la région T située en dessous du nuage prend une charge (+) par influence. Par conséquent, des lignes de champ et une d.d.p. s'établissent entre le bas du nuage et la surface de la terre.
D'autres lignes de champ réunissent les électrons chassés de la région T aux charges positives situées au sommet du nuage, créant à quelques kilomètres du nuage un champ électrique de sens opposé à celui qui règne juste en dessous.
À mesure que le transfert de charges se poursuit à l'intérieur du nuage, le champ électrique en dessous devient très fort, pouvant atteindre à certains points la valeur critique d'ionisation de 3 MV/m. Ce phénomène, qui se produit au-dessus des clochers d'église et des grands arbres, etc., dégage parfois une lumière bleuâtre.
Les marins qui autrefois observaient le phénomène autour des mâts de leur bateau l'appelaient le feu Saint-Elme. Lorsque le champ devient assez intense, un éclair jaillit entre le nuage et la terre. La décharge d'un éclair est accompagnée d'un transfert d'électricité de 0,2 à 20 coulombs sous une tension de plusieurs centaines de millions de volts.
Le courant atteint sa valeur crête en 1 à 2 microsecondes et décroît à la moitié de sa valeur crête en 50 microsecondes environ. Ce que l'on observe comme un seul éclair est souvent composé de plusieurs éclairs qui se succèdent rapidement. La décharge totale peut ainsi durer jusqu'à 200 ms. Parfois cette décharge a lieu à l'intérieur du nuage plutôt qu'entre le bas du nuage et le sol.
Enfin, plusieurs éclairs se produisent aussi entre les nuages. Le coup de tonnerre est produit par l'onde de choc supersonique créée par l'expansion ultra-rapide de l'air qui entoure l'éclair intensément chaud.
Paratonnerres
Les paratonnerres sont simplement des tiges de métal qui dépassent la partie la plus haute d'une structure, afin de canaliser la foudre vers le sol par l'entremise d'un fil conducteur.
On réussit de cette manière à empêcher que le courant intense suive un chemin aléatoire dans la structure, ce qui pourrait provoquer un incendie ou présenter un danger pour les occupants. Un paratonnerre n'est pas sans danger ; pendant une décharge il peut créer des hautes tensions près du sol, et on doit se garder d'être proche du fil conducteur pendant les orages.
Chocs de foudre sur les lignes de transport
Lorsque la foudre frappe directement une ligne de transport, elle dépose sur celle-ci une charge électrique importante de sorte qu'une énorme surtension apparaît immédiatement entre la ligne et la terre. La rigidité diélectrique de l'air se trouve alors dépassée, un arc de décharge s'établit et la ligne se décharge à la terre.
Le tout se passe en moins de 50 µs. L' arc déclenché par la foudre produit un éclair et crée une région ionisée entre la ligne et la terre. Cette région se comporte comme un court-circuit. La tension alternative du réseau fournit alors un courant de court-circuit qui maintient l'arc jusqu'à l'ouverture des disjoncteurs en bout de ligne.
Les disjoncteurs les plus rapides ouvrent le circuit en 1/15e de seconde, soit un temps 1000 fois plus long que la durée de l'éclair qui a touché la ligne.
Il est assez rare qu'une ligne soit frappée directement ; il arrive plus souvent que la foudre frappe le fil de garde qui est placé au-dessus de la ligne ou, encore, qu'il frappe un objet situé dans le voisinage.
Dans ces circonstances, la ligne se charge par influence, ce qui produit encore une surtension locale importante mais moins élevée que dans le cas d'un coup direct. Cette charge, d'abord concentrée, se divise en deux (Fig . 20-16) pour former deux ondes qui filent en sens opposés, à une vitesse voisine de celle de la lumière (300 m/µs).
Figure 20-16 Ondes de tension de choc se propageant sur une ligne de transport. L'onde de gauche atteindra le poste de transformation en quelques microsecondes
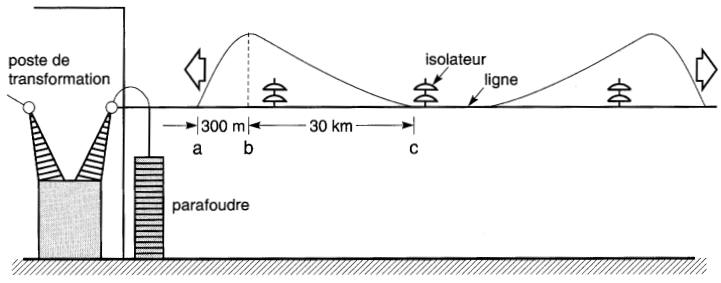
À tout instant, la hauteur de l'onde à chaque point de la ligne représente la tension qui existe entre la ligne et la terre. La tension crête correspondant au sommet de l'onde peut atteindre 1 ou 2 millions de volts. Le front ab de l'onde s'étend sur une distance de 300 m alors que la queue bc s'allonge sur quelques dizaines de kilomètres.
L'onde représente aussi, à chaque point, la valeur du courant dans la ligne. Pour la plupart des lignes aériennes, le rapport entre la tension et le courant correspond à une résistance de 400Ω environ; une tension momentanée et locale de 800 000V est donc accompagnée d'un courant momentané et local de 800 000 / 400 = 2000A.
À mesure que l'onde se propage sur la ligne, les importantes pertes par effet Joule et par effet couronne aplatissent la forme de l'onde et diminuent sa tension crête. Lorsque l'onde rencontre un isolateur sur un pylône, l'isolateur subit un choc de tension violent mais de courte durée.
En effet, la tension peut monter de sa valeur normale à quelques centaines de kilovolts en 1 µs, ce qui correspond à la longueur du front ab de l'onde.
Si l'isolateur est incapable de résister à cette surtension, il se produit un arc et, comme dans le cas d'un coup direct, les disjoncteurs doivent ouvrir le circuit.
Si, par contre, l'isolateur supporte la surtension, l'onde se propage plus loin pour aboutir finalement à un poste de transformation.
C'est là que son arrivée foudroyante peut produire des ravages. La surtension sur les transformateurs, les compensateurs, etc., peut endommager leurs enroulements et les mettre hors service. Elle peut également endommager les disjoncteurs, sectionneurs, isolateurs, relais, etc., faisant partie du poste.
Pour cette raison, il faut pré- voir des parafoudres à l'entrée d'un poste de transformation pour réduire le niveau de la surtension avant que l'onde de choc n'atteigne l'appareillage critique. Les parafoudres sont conçus pour écrêter la surtension afin qu'elle n'excède pas une valeur prédéterminée, di- sons 400 kV.
L'équipement lourd à l'intérieur du poste est conçu pour supporter une tension impulsionnelle nettement supérieure à 400 kV, disons 550 kV.
Par conséquent, si une onde de surtension de 1000 kV arrive au poste de transformation, le parafoudre absorbe une bonne partie de l'énergie qu'elle contient. L'onde qui se propage au-delà du parafoudre n'aura alors qu'une valeur crête de 400 kV. Comme l'équipement lourd peut supporter 550 kV, il ne sera pas endommagé.
Tension de tenue aux ondes de choc, BIL. (BIL: abréviation anglaise pour «basic impulse insulation level»)
Les recherches ont démontré que les matériaux isolants peuvent supporter des tensions particulièrement élevées si elles sont de courte durée.
Par exemple, supposons que l'on désire tester la qualité de l'isolation d'un transformateur en appliquant une tension de 60 Hz entre un de ses enroulements et la terre. À mesure que l'on augmente la tension, on atteindra un point où l'isolation claquera, disons à une tension crête de 65 kV.
Par contre, si on lui applique une tension continue de courte durée (de l'ordre de quelques microsecondes), on s'aperçoit que l'isolation peut tolérer une tension crête presque deux fois plus élevée, soit environ 130 kV.
Les essais ont démontré que les isolateurs, sectionneurs, interrupteurs, compensateurs, disjoncteurs, etc., se comportent essentiellement de la même façon. Étant donné que les ondes de chocs dues à la foudre sont toujours de courte durée, on a établi des normes concernant ce genre de surtension.
En effet, tout appareil électrique doit pouvoir résister à une onde de choc ayant une forme et une valeur crête appropriées. À cette fin, les organismes de normalisation ont établi une onde de tension de choc standard présentée à la Fig. 20-17.
Figure 20-17 Forme d'onde standard et valeurs normalisées de la tension de choc
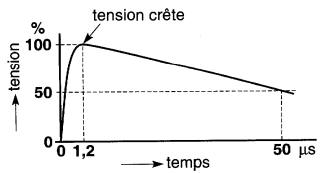
Cette onde de foudre atteint sa valeur crête en 1,2 µs et décroît à la moitié de cette valeur en 50 µs. Pour cette raison, l'onde est habituellement désignée par l'appellation « 1,2 X50».
La tension crête peut prendre une série de valeurs normalisées comprises entre 30 kV et 2400 kV; quelques-unes sont affichées au tableau 20-1.
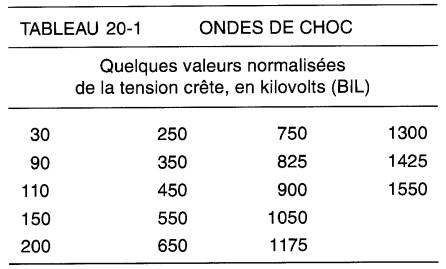
Ainsi, tout appareil qui peut résister à une onde de choc de 900 kV est dit posséder une tension de tenue au choc (ou BIL) de 900 kV. La tension de choc est plusieurs fois plus élevée que la tension nominale de l'appareil.
Par exemple, un transformateur de distribution de 69 kV doit pouvoir résister à une tension de choc de 350 kV. Cependant, il n'y a pas de rapport fixe entre la tension de choc et la tension nominale.
Notons qu'à mesure que la tension de choc augmente, on doit augmenter la quantité d'isolation, ce qui augmente la grosseur et le coût de l'appareil. Les parafoudres et les tiges de décharge protégeant les appareils électriques doivent écrêter toute tension supérieure à leur tension de tenue au choc.
Ainsi, un transformateur ayant un BIL de 900 kV doit être protégé par des parafoudres qui écrêtent la tension à une va- leur sensiblement inférieure à 900 kV.
Résumé
Cette section nous a fait découvrir plusieurs phénomènes de l'électrostatique gouvernant le comportement des corps chargés.
Lorsque des charges sont transférées d'un corps à un autre, il s'établit entre ces deux corps une différence de potentiel, ou tension électrique. L'unité SI de charge électrique est le coulomb (C).
De la même façon qu'un conducteur parcouru par un courant est entouré d'un champ magnétique, deux corps chargés d'électricité de signes contraires créent un champ électrique. Le spectre de ce champ électrique est composé de lignes de force partant des charges positives (+) et aboutissant sur des charges négatives (-).
Ce champ électrique contient une énergie électrostatique qui dépend de la tension entre les deux corps et de la charge transférée. Une particule chargée placée dans un champ électrique subira une force qui l'oblige à se déplacer le long des lignes de force du champ.
Ce phénomène peut être mis à profit dans plusieurs appareils (dépoussiérage, peinture, . . .) . Il peut aussi provoquer l'ionisation d'un gaz isolant comme l'air lorsqu'il est traversé par un champ électrique intense. Le phénomène d'ionisation provoque les éclairs pendant les orages.
L'ionisation cause des pertes par effet couronne le long des lignes de transport. Lorsque la foudre frappe une ligne, la charge importante déposée sur la ligne peut développer des surtensions dangereuses pour les équipements du réseau. La forme d'onde de tension caractéristique des ondes de choc dues à la foudre a été normalisée.
De plus, l'isolation des équipements doit être conçue pour supporter un certain «BIL » correspondant à la tension crête de l'onde de choc normalisée. Les parafoudres permettent de protéger les équipements des postes en limitant les surtensions à une valeur inférieure à leur BIL.
PROBLÈMES
Niveau pratique
20-1 Est-ce que l'énergie dans un champ électrique réside sur les corps chargés ou dans l'espace qui les sépare?
20-2 Donner deux méthodes permettant de transporter une charge électrique entre deux corps.
20-3 Peut-on transporter des charges entre deux corps métalliques? entre deux corps en plastique?
20-4 Expliquer le principe du précipitateur électro- statique.
20-5 Que veut dire tension de tenue au choc?
Niveau intermédiaire
20-6 Après avoir transporté une charge de 1 µC entre les corps de la Fig. 20-1, on constate que la tension entre eux est de 50 kV.
a) Quelle est l'énergie dans le champ électrique?
b) Si, en court-circuitant les corps, la décharge se fait en 1 µs, calculer la puissance moyenne dissipée.
c) Quelle est l'énergie dissipée en (b)?
20-7 Lorsqu'on branche la pile sur les deux corps de la Fig. 20-6, on constate qu'il s'effectue un transfert de 1012 électrons. Calculer l'énergie dans le champ élec- trique.
20-8 Dans la Fig. 20-3a, on constate qu'après avoir effectué un transfert de 20 RC, la tension entre les deux corps est de 8 kV.
Lorsqu'on éloigne les deux corps l'un de l'autre (Fig. 20-3b), on constate que la tension augmente à 12 kV.
Calculer:
a) l'énergie emmagasinée dans le champ électrique avant et après avoir éloigné les deux corps
b) le travail mécanique exercé lors de la séparation des corps
20-9 Dans la Fig. 20-9a, chaque ligne de force aboutit sur une charge de 4 µC.
a) Calculer la tension entre les plaques sachant que l'énergie totale dans le champ est de 4 mJ .
b) Si l'on augmente la distance entre les plaques, le nombre de lignes change-t-il?
20-10 La tension entre les plaques de la Fig. 20-9a est de 2 kV.
a) Calculer la valeur du champ électrique, sachant que la distance séparant les plaques est de 2 mm.
b) Une particule de poussière portant une charge négative de 3 pC (pico coulombs) se trouve entre les deux plaques. Quelle est la force agissant sur la particule? Dans quel sens agit-elle?
20-11 En touchant une poignée de porte, une personne fait jaillir un arc ayant une longueur de 1 cm. À quelle tension la personne était-elle chargée par rap- port au sol? Pourquoi ce choc n'est-il pas mortel?
Niveau avancé
20-12 Dans la Fig. 20-9e, le champ électrique près de la tige est de 2 kV/mm alors qu'il est de 500 V/mm près de la plaque. Calculer la force agissant sur un électron qui se trouve:
a) près de la tige
b) près de la plaque
20-13 a) Tracer la forme d'onde d'une onde de choc normalisée ayant une tension crête de 1300 kV . b) Quelle est la tension après 1,2 µs? après 50 µs?
20-14 Dans la Fig. 20-15, la charge terrestre située immédiatement au-dessous du nuage est de 40 coulombs. Sachant que la tension entre le bas du nuage et le sol est de 100 MV, calculer l'énergie contenue dans le champ, en kW.h.
20-15 Une onde de choc ayant la forme indiquée à la Fig. 20-17 et possédant une valeur crête de 90 kV se propage sur une ligne de transport ayant une résistance caractéristique de 400Ω.
Calculer:
a) la longueur du front de l'onde de choc
b) la longueur de la queue de l'onde de choc entre 100 % et 50 % de la tension crête
c) le courant maximal dans la ligne
20-16 Calculer la masse d'un grain de poussière sphérique ayant un diamètre de 8 µm, sachant que sa masse volumique est de 3000 kg/m³. Calculer la force exercée par la gravité sur la poussière (en newtons).
20-17 Le grain de poussière du problème 20-16 porte une charge de 800 électrons et se trouve dans un champ électrique de 2,4 kV/mm.
a) Calculer la force électrostatique (en newtons) agissant sur la poussière;
b) De combien de fois cette force excède-t-elle la force due à la gravité?
20-18 En se référant à la Fig. 20-10, on donne: R1 = 4 mm, R2 = 6 mm, tension entre le conducteur central et le cylindre métallique = 2400V.
Calculer:
a) la valeur moyenne du champ électrique (V/m) entre le conducteur et le cylindre
b) le champ électrique à la surface du conducteur
c) le champ électrique à la surface intérieure du cylindre
d) Est-ce que l'air est ionisé près du conducteur?
e) Quelle tension minimale doit-on appliquer entre le cylindre et le conducteur central pour que l'air s'ionise à la surface du conducteur?
Réponses
6a) 25 mJ; 6b) 25 kW; 6c) 25 mJ;
7) 8 µJ; 8a) 80 mJ; 120 mJ;
8b) 40 mJ; 9a) 286 V; 9b) non; 10a) 1 MV/m; 1
Ob) 3 µN; vers A;
11) 30 kV; charge trop faible; 12a) 0,32 pN; 12b) 0,08 pN;
13a) voir Fig. 20-17; 13b) 1300 kV; 650 kV; 14) 556 kWh;
15a) 360 m;
15b) 14,64 km; 15c) 225 A; 16) 8 x 10-13 kg; 7,9 pN;
17a) 310 pN; 17b) 39,5
fois; 18a) 1,2 MV/m; 18b) 1,48 MV/m;
18c) 0,987 MV/m; 18d) non; 18e) 4865 V
