Forces électromagnétiques

Électrotechnique

Lorsqu'un conducteur portant un courant est orienté convenablement dans un champ magnétique, il est soumis à une force que l'on appelle force électromagnétique.

Ce phénomène est d'une importance capitale car il est à la base du fonctionnement des moteurs, des haut-parleurs et d'un grand nombre d'appareils de mesure. Étudions d'abord le cas d'un conducteur rectiligne.

 Sens de la force agissant sur un conducteur rectiligne

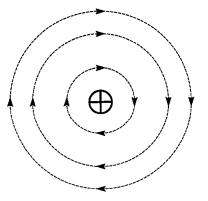
On a vu au à la section Courants électriques et champs magnétiques qu'un conducteur rectiligne parcouru par un courant s'entoure d'un champ magnétique. Pour un courant entrant dans la page, les lignes de force auraient le sens indiqué à la Fig. 16-1.

Figure 16-1 Champ magnétique autour d'un conducteur lorsque le courant entre dans la page

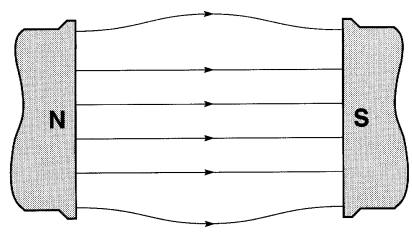
D'autre part, la Fig. 16-2 montre le champ magnétique créé entre les deux pôles d'un aimant permanent puissant.

Figure 16-2 Champ magnétique entre les pôles d'un aimant permanent

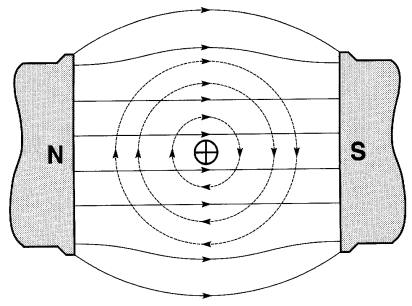
Si l'on place ce conducteur, parcouru par un courant, entre les pôles de l'aimant permanent (Fig. 16-3),

Figure 16-3 Superposition des champs magnétiques.

Les lignes de force agissent dans le même sens au-dessus du conducteur, ce qui augmente la densité de flux à cet endroit. Les lignes de force agissent en sens contraires en dessous du conducteur de sorte que la densité de flux est réduite à cet endroit

on constate que:

1. le conducteur est soumis à une force qui tend à le déplacer vers le bas

2. si l'on change le sens du courant, le sens de la force change également

3. la force agit dans une direction qui est à la fois perpendiculaire à la direction du courant et à celle des lignes de force

L'aspect du champ magnétique résultant n'est évidemment pas semblable à celui donné à la Fig. 16-3 car comme nous l'avons vu au à la section Magnétisme, les lignes de flux ne se croisent jamais.

Cependant, on observe que les lignes de force du champ magnétique créé par le conducteur et celles du champ magnétique créé par l'aimant permanent sont de même sens au-dessus du conducteur, et de sens contraires en dessous.

Il en résulte une augmentation du nombre de lignes au-dessus du conducteur et une diminution en dessous ; le champ magnétique résultant a donc l'aspect donné à la Fig. 16-4.

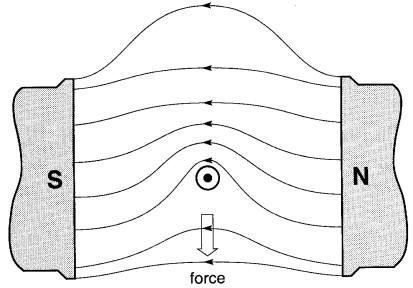
Figure 16-4 Spectre du champ magnétique résultant

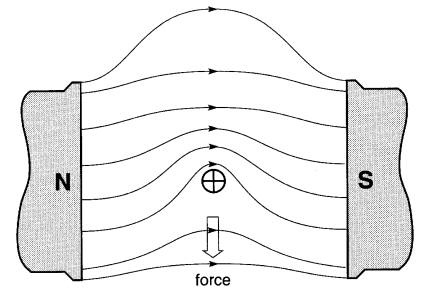
Rappelons que les lignes de force sont comme des fils élastiques tendus qui se repoussent ; lorsqu'elles sont concentrées au-dessus du conducteur, la force de répulsion qui existe entre elles tend à repousser le conducteur vers le bas.

Cet artifice qui permet de déterminer le sens de la force peut servir de règle. De cette façon, on vérifiera que la force agissant sur le conducteur de la Fig. 16-4 a bien le sens indiqué. Le sens de la force dépend donc du sens du courant et de celui du champ.

Si l'on inverse à la fois le sens du courant et celui des lignes de force, le sens de la force mécanique reste inchangé (comparez les Figs. 16-4 et 16-5).

Figure 16-5 Lorsque la direction du champ et le sens du courant sont inversés, le sens de la force demeure le même

Intensité de la force

On peut démontrer expérimentalement que l'intensité de la force qui agit sur un conducteur parcouru par un courant et placé dans un champ magnétique dépend:

a) de l'intensité du courant: plus le courant est intense, plus la force est grande

b) de la densité de flux du champ magnétique : plus la densité des lignes est grande, plus la force est intense

c) de la longueur du conducteur traversant le champ magnétique: plus le conducteur actif est long, plus la force est grande. Par conducteur actif on entend la partie du conducteur qui se trouve dans le champ magnétique.

d) de la direction du conducteur par rapport à celle du champ:

la force est maximale quand le conducteur est perpendiculaire aux lignes de force (Fig. 16-6) et nulle quand il est parallèle au champ (Fig. 16-7); entre ces deux positions, l'intensité de la force prend des valeurs intermédiaires.

Figure 16-6 La force sur un conducteur est maximale lorsque le conducteur est perpendiculaire au champ magnétique

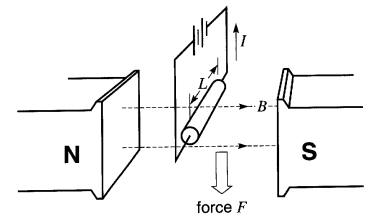
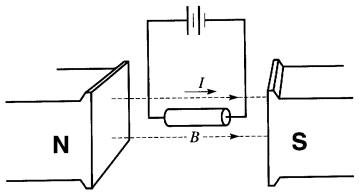
Figure 16-7 La force sur un conducteur est nulle lorsque le conducteur est parallèle au champ magnétique

La valeur maximale de la force électromagnétique F agissant sur un conducteur rectiligne de longueur l parcouru par un courant I et placé dans un champ de densité B, est donnée par l'équation:

F = BlI    (16-1)

où

F = force agissant sur le conducteur [N]

B = densité de flux, en teslas [T]

l = longueur du conducteur actif dans le champ [m]

I = courant circulant dans le conducteur [A]

Exemple 16-1

Calculer la force qui agit sur un conducteur de 1,2 m de long, parcouru par un courant de 200 A et placé dans un champ magnétique dont la densité de flux est 0.5 tesla.

Le conducteur est perpendiculaire aux lignes de force (Fig. 16-6).

Solution

La force est:

F = BlI = 0,5 x 1,2 x 200 = 120 N

Électrons et champ magnétique

Afin d'expliquer la façon dont les forces électromagnétiques prennent naissance, considérons un électron placé dans un champ magnétique. Lorsque l'électron est stationnaire, le champ magnétique ne l'influence pas.

Cependant, si l'électron se déplace dans le champ, il subira une force dont l'intensité dépend de sa vitesse et de la densité du champ. La direction de la force est à la fois perpendiculaire au trajet de l'électron et aux lignes de force du champ magnétique.

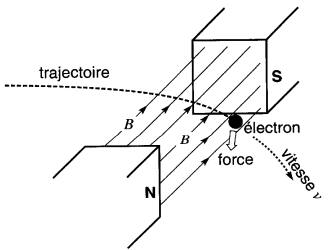
Par exemple, l'électron de la Fig. 16-8 déviera vers le bas lorsqu'il traversera le champ.

Figure 16-8 Force sur un électron en mouvement et trajectoire résultante

Les lois de la physique nous indiquent que cette force, extrêmement faible, peut être calculée par la formule suivante :

F = evB     (16-2)

où

F = force exercée sur l'électron [N]
e = charge de l'électron (1,6 x 10-19 coulomb)
v = vitesse de l'électron [m/s]
B = densité de flux, en teslas [T]

Bien que cette force soit très faible, elle réussit néanmoins à donner une courbure appréciable à la trajectoire de l'électron car sa masse est minuscule. Il est facile d'observer les conséquences de cette déflection en approchant un aimant permanent de l'écran d'un oscilloscope ou d'un téléviseur.

Les électrons libres se déplaçant à l'intérieur d'un conducteur subissent exactement les mêmes forces lorsque le conducteur est placé dans un champ magnétique. Comme ces électrons ne peuvent quitter le corps métallique du conducteur, il s'ensuit que la force agissant sur chacun d'eux est transmise à celui-ci.

Les électrons se déplacent très lentement à l'intérieur d'un conducteur, par conséquent ils sont soumis à des forces extrêmement faibles. Cependant, leur nombre est si considérable que toutes ces forces élémentaires produisent une force totale assez intense.

Force entre deux conducteurs

On a vu, d'une part, qu'un courant traversant un conducteur s'entoure d'un champ magnétique et, d'autre part, qu'un conducteur parcouru par un courant est soumis à une force lorsqu'il est placé dans un champ. Il doit donc nécessairement s'exercer une force sur deux conducteurs voisins parcourus chacun par un courant.

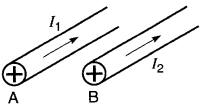
Ce phénomène est, en réalité, un cas particulier de l'action d'un champ magnétique sur un courant électrique. Soit deux conducteurs parallèles parcourus par des courants I₁ et I₂ de même sens (Fig. 16-9a).

Figure 16-9a Deux conducteurs portant des courants circulant dans le même sens

La forme des lignes de force autour de chacun des conducteurs considérés individuellement est donnée à la Fig. 16-9b.

Figure 16-9b Superposition des champs magnétiques créés par les deux courants

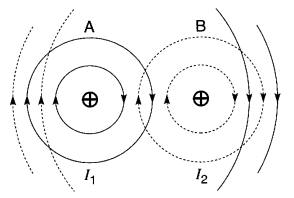
On constate que, dans l'espace compris entre les deux conducteurs, les lignes créées par Ii sont en sens inverse de celles créées par I₂.

Par conséquent, entre les conducteurs le champ magnétique sera relativement faible.

Cependant, à l'extérieur des conducteurs, les lignes provenant des deux courants ont tendance à se renforcer. Le spectre des lignes de force résultant de l'action mutuelle de ces deux champs magnétiques est montré à la Fig. 16-9c.

Figure 16-9c Spectre du champ magnétique résultant lorsque les deux courants pénètrent dans la page. Les conducteurs s'attirent mutuellement

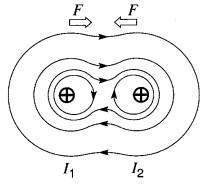
Sachant que les lignes de force se comportent comme des bandes élastiques tendues et poussant l'une sur l'autre, on constate que les conducteurs sont soumis à des forces qui tendent à les rapprocher.

Par contre, si les courants I₁ et I₂ circulent en sens inverses (Fig. 16-10a), les lignes de flux se renforcent dans l'espace compris entre les conducteurs (Fig. 16-10b). Le spectre résultant est montré à la Fig. 16-10c.

Figure 16-10a Deux conducteurs portant des courants circulant en sens inverses

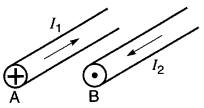
Figure 16-1Ob Superposition des champs magnétiques crées par les deux courants

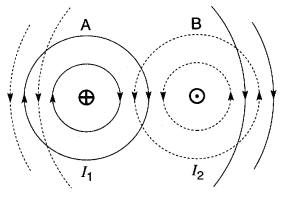
Figure 16-1 Oc Spectre du champ magnétique résultant lorsque les courants traversent la page en sens inverses. Les conducteurs se repoussent mutuellement

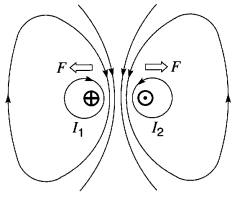
Si l'on applique la même règle aux lignes de force du spectre de la Fig. 16-10c, on vérifiera que deux conducteurs parallèles parcourus par des courants de sens contraires tendent à se repousser.

Connaissant la valeur des courants I₁ et I₂ parcourant chacun des conducteurs et la distance d qui les sépare, on peut calculer la force agissant sur chacun d'eux.

En effet, d'après la section Courants électriques et champs magnétiques, un courant I₁ produit à une distance d un champ dont la densité de flux (en teslas) est:

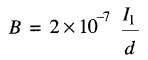
de plus, on a vu que la force agissant sur un conducteur parcouru par un courant I₂ , vaut :

F = BlI₂

d'où

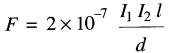    (16-3)

où

F = force entre deux conducteurs parallèles [N]

I₁,I₂ = courants circulant dans les conducteurs [A]

l = longueur des conducteurs [m]

d = distance séparant les conducteurs [m]

Exemple 16-2

Deux barres omnibus cylindriques de 3 mètres de long portent un courant normal de 1000 A.

Calculer la force d'attraction lors d'un courant de court-circuit de 60 000 A sachant qu'elles sont séparées par une distance de 10 cm.

Solution

D'après la formule 16-3, on obtient :

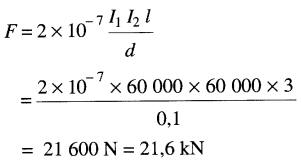
On constate que les barres omnibus sont soumises à une force considérable lors d'un court-circuit. Elles sont donc sujettes à une certaine déformation.

Cas d'un cadre rectangulaire

Soit un cadre conducteur ABCD (Fig. 16-11), parcouru par un courant et placé entre les deux pôles d'un aimant. La densité de flux provenant de l'aimant est uniforme.

Figure 16-11 Cadre placé dans un champ magnétique. Des forces agissent sur les côtés AB et CD, elles sont nulles sur les côtés AD et BC

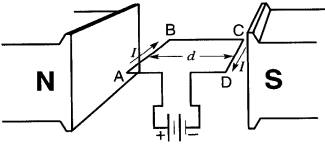
En appliquant à chacun des conducteurs AB et CD, la règle vue à la section 16.1, on voit que les forces électromagnétiques F1 et F2 sont égales, mais agissent en sens contraires.

La force est nulle sur les côtés AD et BC car ces conducteurs sont orientés dans la même direction que les lignes de force. Le cadre est donc soumis à un couple tendant à le faire tourner (Fig. 16-12).

Figure 16-12 Les forces agissant sur les côtés AB et CD du cadre produisent un couple qui tend à le faire tourner

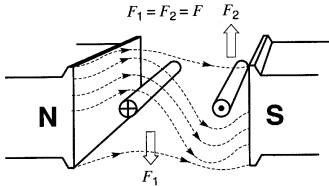
Si l'on change le sens du courant dans le cadre, celui-ci cherchera à tourner dans le sens contraire.

La valeur du couple est donnée par l'expression

T = Fd    (16-4)

où

T = couple, en newtons-mètres [N'm]
F = force agissant sur chaque conducteur actif, en newtons [N]
d = distance séparant les conducteurs actifs, en mètres [m]

Si le cadre possède N spires au lieu d'une seule, le couple sera N fois plus grand, soit :

T = NFd

Exemple 16-3

La bobine rectangulaire de la Fig. 16-13 possède 40 spires et porte un courant de 10 A.

Figure 16-13 Voir exemple 16-3

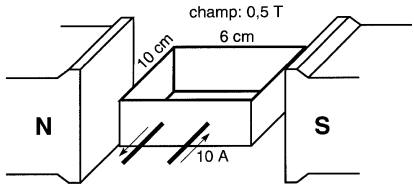
Les côtés AB et BC du cadre ont respectivement une longueur de 10 cm et de 6 cm. Sachant que la densité de flux dans l'entrefer de l'aimant est de 0,5 tesla, calculer le couple agissant sur le cadre.

Solution

La force s'exerçant sur les conducteurs AB et CD vaut :

F = BlI = 0,5 x 0,1 x 10 = 0,5 N

Chaque côté actif du cadre (composé de 40 conducteurs) est donc soumis à une force de F = 40 x 0,5 = 20N d'où le couple:

T = Fd = 20 x 0,06 = 1,2 N.m

Conséquences des forces entre les courants

1. Force sur deux conducteurs parallèles

Normalement, les forces qui s'exercent sur les deux conducteurs alimentant une charge sont de faible intensité.

Cependant, dans le cas d'un court-circuit, elles peuvent atteindre des valeurs de plusieurs kilonewtons si les conducteurs sont parallèles sur une grande distance (cas des lignes de transport) ou si les intensités des courants de court-circuit sont énormes (cas des barres omnibus dans les centrales et postes électriques).

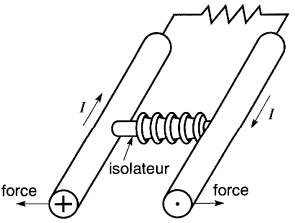
Pour éviter que les barres omnibus soient déformées par l'action de cette force, on les ancre solidement à une structure et quelquefois même, on les fixe ensemble au moyen d'isolateurs rigides (Fig. 16-14).

Figure 16-14 Un isolateur fixé entre deux conducteurs les empêche de se déformer lors d'un court-circuit

2. Force sur les spires d'une bobine

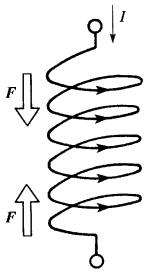
Force sur les spires d'une bobine Les spires de la bobine de la Fig. 16-15 sont parcourues par des courants parallèles et de même sens. Il en résulte des forces d'attraction entre les spires qui tendent à comprimer la bobine.

Figure 16-15 Le courant circulant dans une bobine produit des forces tendant à la comprimer

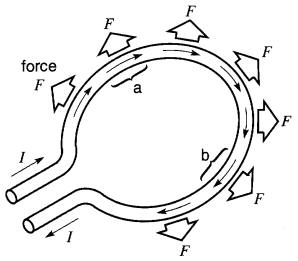
D'autre part, les courants circulant en sens inverses dans les sections diamétralement opposées d'une même spire (comme a et b de la Fig. 16-16) se repoussent mutuellement, ce qui tend à déformer la spire en l'élargissant.

Figure 16-16 Le courant circulant dans une spire produit des forces qui tendent à la dilater.

C'est pour éviter les effets destructifs de telles forces de compression et de dilatation lors d'un court-circuit que l'on prend soin de cheviller solidement les spires des enroulements d'un transformateur.

3. Force sur un sectionneur

Lorsqu'un courant intense traverse un sectionneur (Fig. 16-17), les forces électromagnétiques F1, F2, F3, F4, et F5 agissent sur les conducteurs.

Figure 16-17 Lorsqu'un courant intense circule dans un sectionneur la force F4 tend à ouvrir la lame

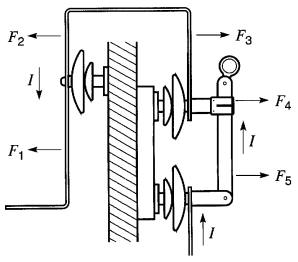
En particulier, la force F4 tend à faire ouvrir la lame. Ces appareils doivent être munis d'un dispositif de blocage pour prévenir toute ouverture accidentelle.

Applications des forces électromagnétiques L'application la plus importante des forces électromagnétiques est le moteur électrique qui sera le sujet de chapitres subséquents.

Les appareils de mesure étudiés au chapitre 6 utilisent également les effets électromagnétiques. Parmi les nombreuses autres applications de ces forces, citons le haut-parleur et le soufflage magnétique d'un arc électrique.

Le haut-parleur électromagnétique (Fig. 16-18) est composé essentiellement d'une bobine légère, solidaire d'un diaphragme, et logée dans l'entrefer d'un aimant permanent.

Figure 16-18 Le courant alternatif circulant dans les spires d'une bobine de haut-parleur produit une force verticale qui agit tantôt vers le haut, tantôt vers le bas. Cette force alternative varie rapidement, ce qui fait vibrer le diaphragme

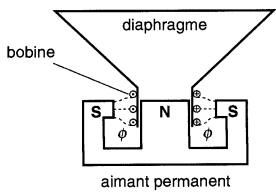
Lorsqu'un courant circule dans la bobine, une force électromagnétique agit sur celle-ci et entraîne le déplacement du diaphragme. Ce déplacement suit les variations rapides du courant dans la bobine et il est d'autant plus grand que ce courant est plus intense.

Les mouvements successifs du diaphragme provoquent la vibration de l'air environnant et, par suite, la production d'un son. L'action d'un champ magnétique sur un arc électrique (passage du courant dans l'air) est mise à profit dans les disjoncteurs du type à soufflage magnétique (Fig . 16-19).

Figure 16-19 Soufflage magnétique d'un arc électrique

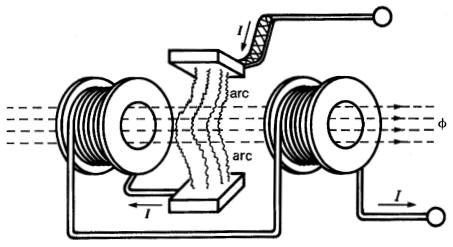
L'arc créé à l'ouverture est ainsi soumis à une force électromagnétique qui allonge l'arc et le pousse vers une série de séparateurs qui en provoquent l'extinction.

Étant donné que cette force intense agit sur un arc dont la masse est très faible, il s'ensuit que cet arc se déplace extrêmement vite, dépassant même la vitesse du son. Le «soufflage» de l'arc est donc très efficace.

Résumé

Dans cette section nous avons appris qu'un conducteur parcouru par un courant et placé dans un champ magnétique est soumis à une force électromagnétique . Cette force, qui peut être calculée par une formule simple, dépend du courant, de la densité de flux magnétique, de la longueur et de l'orientation du conducteur par rapport aux lignes de force.

Comme un conducteur parcouru par un courant crée aussi son propre champ magnétique, il s'ensuit que des conducteurs voisins sont soumis à des forces d'attraction ou de répulsion qui dépendent des sens des courants.

Ces forces électromagnétiques trouvent de nombreuses applications dont la plus importante est le moteur électrique. Elles peuvent aussi avoir tendance à déformer des circuits parcourus par des courants intenses.

PROBLÈMES

Niveau pratique

16-1 Expliquer ce que nous avons appelé, le deuxième principe de l'électromagnétisme .

16-2 De quoi dépend l'intensité de la force s'exerçant sur un conducteur parcouru par un courant et placé dans un champ magnétique?

16-3 Lorsqu'un courant très intense parcourt une bobine de fil flexible, la bobine se rétrécit. Expliquer.

16-4 Donner trois applications de l'action entre les courants électriques et les champs magnétiques.

16-5 Dessiner l'allure des lignes de force entre les pôles de l'aimant de la Fig. 16-20. Indiquer le sens de la force s'exerçant sur le conducteur.

Figure 16-20 Voir problème 16-5

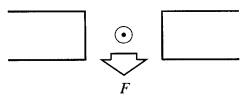
16-6 Indiquer la polarité magnétique de l'aimant de la Fig. 16-21 sachant que le conducteur est soumis à une force F dirigée vers le bas.

 Figure 16-21 Voir problème 16-6

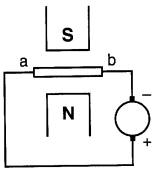
16-7 Quel est le sens de déplacement du conducteur ab dans la Fig. 16-22?

Figure 16-22 Voir problème 16-7

Niveau intermédiaire

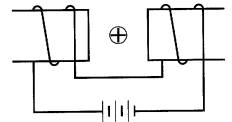
16-8 L'électro-aimant de la Fig. 16-23 est raccordé à une pile sèche.

Quel est le sens de la force qui agit sur le conducteur placé entre les pôles de l'électro-aimant?

Qu'arrivera-t-il si le sens du courant dans le conducteur est inversé?

Figure 16-23 Voir problème 16-8

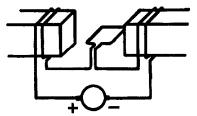
16-9 Quel est le sens de rotation de la boucle de la Fig. 16-24 (horaire ou antihoraire)?

Qu'arrivera-t-il si les bornes de la génératrice sont interverties?

Figure 16-24 Voir problème 16-9

16-10 Un conducteur portant un courant de 2 kA se trouve dans un champ magnétique dont la densité de flux est 0,5 tesla. Quelle force sera produite par mètre de conducteur actif?

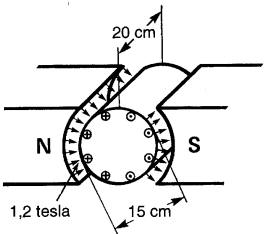
16-11 La Fig. 16-25 est une représentation schématique d'un moteur électrique. Le cylindre porte 100 conducteurs dont l'ensemble constitue effectivement un cadre à 50 spires. Les conducteurs ont une longueur active de 200 mm. ils sont parcourus par un courant de 50 ampères et ils sont placés dans un champ de 1,2 T.

Calculer la force agissant sur chacun d'eux ainsi que le couple résultant.

Figure 16-25 Voir problème 16-11

16-12 Dans la Fig. 16-17, la lame du sectionneur est à une distance de 0,5 m du conducteur vertical et sa longueur est de 300 mm. Calculer la force agissant sur la lame pour le courant nominal de 3 kA et pour un courant de court-circuit de 200 kA.

16-13 La bobine de soufflage de la Fig. 16-19 produit une densité de flux de 50 mT lorsqu'elle porte le courant nominal de 120 A. Lors d'un court-circuit, le courant monte à 6000 A et le disjoncteur ouvre ses con- tacts.

Calculer la force agissant sur l'arc lorsque sa longueur est de 10 mm.

16-14 Dans la Fig. 16-14, si le courant change de sens, dans quelle direction les forces agiront-elles?

16-15 Si le conducteur de la Fig. 16-3 porte un courant alternatif, la force moyenne résultante est nulle. Expliquer.

16-16 La bobine du haut-parleur de la Fig. 16-18 comprend 2000 spires portant un courant maximal de 100 mA. Si le diamètre de la bobine est de 25 mm, calculer la force transmise au diaphragme, sachant que 1a densité de flux créée par l'aimant est de 0,6 T.

16-17 Un mouvement d' Arsonval donnant une pleine déviation pour un courant de 100 µA possède les caractéristiques suivantes (voir Fig . 6-1):

Figure 6-1 Composants d'un mouvement d'Arsonval

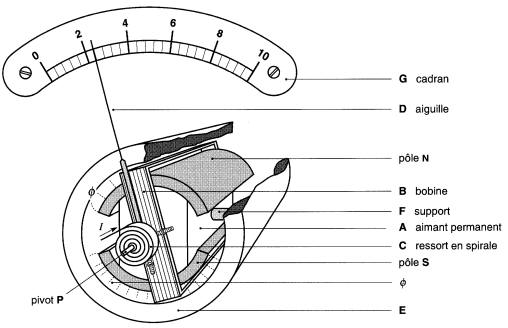
Noyau E en fer doux

diamètre intérieur: 21,8 mm
diamètre extérieur: 28,0 mm
longueur axiale: 14,5 mm

Pièces polaires N S en fer doux

diamètre extérieur: 18,7 mm
longueur axiale: 11,7 mm
longueur de l'arc extérieur: 21,0 mm

Bobine

longueur diamétrale : 20,8 mm
longueur axiale: 14,5 mm
largeur: 4,2 mm
nombre de spires : 600
résistance à 20 °C: 1500Ω
matériau: cuivre

Aimant permanent

longueur diamétrale: 15 mm
longueur axiale 11,7 mm
largeur: 10,8 mm
matériau: alnico V

D'après ces données, calculer:

a) la grosseur AWG du fil de la bobine

b) la FMM développée par l'aimant permanent si H = 47 kA/m

c) la densité de flux dans l'entrefer (la longueur des deux entrefers est de (21,8 - 18,7) = 3,1 mm)

d) le couple agissant sur la bobine pour le courant maximal de 100 µA (on suppose que la longueur effective de chaque côté de la bobine est égale à la longueur axiale des pièces polaires (11,7 mm)).

5) vers le haut; 6) nord à gauche; 7) vers le lecteur;
8) vers le bas; vers le haut; 9) horaire; horaire; 10) 1000 N;
11) 12 N; 90 N.m; 12) 1,08 N; 4800 N; 13) 150 N; 14) même sens;
16) 9,42 N; 17a) 4,87 x 10-4mm² (#50); 17b) 705 A; 17c) 0,284 T;
17d) 4,1 µN.m