
Des circuits qui font des choix
Mes premiers pas en Électronique
La section Comment les circuits comprennent les uns et les zéros était consacré aux uns et aux zéros, et vous avez joué avec les bits et les octets dans quelques projets.
Dans cette section, vous allez créer des circuits qui utilisent des uns et des zéros pour prendre des décisions.
Les portes logiques sont des composants qui vérifient les tensions qui représentent ces uns et ces zéros et produisent une tension correspondante.
Je vais vous montrer quelques types de portes logiques et comment les utiliser pour créer un détecteur de code secret.
C'est seulement logique
La logique est un moyen de tirer une conclusion à partir d'informations que l'on sait vraies ou fausses.
Par exemple, imaginez que vous sachiez que l'affirmation suivante est vraie, sans l'ombre d'un doute :
Affirmation 1 :
S'il y a des oranges dans votre réfrigérateur et que vous avez un presse-agrumes, vous pouvez faire du jus d'orange.
Si vous croyez à l'affirmation précédente, deux conditions doivent être vérifiées avant de pouvoir faire du jus d'orange :
Condition 1 : Il y a des oranges dans votre réfrigérateur.
Condition 2 : Vous avez un presse-agrumes.
Si vous examinez votre cuisine et constatez que ces conditions sont vraies, vous pouvez alors conclure logiquement que vous pouvez faire du jus d'orange.
Les ordinateurs utilisent la logique booléenne, un système logique qui fonctionne uniquement avec les valeurs « vrai » et « faux » pour convertir les uns et les zéros en actions.
Pour qu'un ordinateur sache si vous pouvez faire du jus d'orange ou non, il devrait parvenir à cette conclusion grâce à la logique booléenne.
Essayons de penser comme un ordinateur !
Tout d'abord, recherchez les conditions de l'énoncé 1 qui déterminent si vous pouvez faire du jus d'orange ou non.
Dans ce cas, les conditions sont les deux phrases entre « si » et « alors », reliées par « et ».
Attribuez-leur des lettres comme suit :
Il y a des oranges dans votre réfrigérateur = A
Vous avez un presse-agrumes = B
La conclusion est l'énoncé qui suit « alors ». Donnez-lui également une lettre :
Vous pouvez faire du jus d'orange = Q
Avec ces lettres, vous pourriez réécrire l'énoncé 1 comme suit :
« Si A et B, alors Q ».
En abrégé booléen, cela donne :
A ET B = Q
Il s'agit d'une équation logique, où ET est un opérateur comme l'addition ou la soustraction. Lorsque les deux énoncés de chaque côté de ET sont vrais, la conclusion Q est vraie.
Étant donné les conditions 1 et 2, A et B sont tous deux vrais.
En substituant les deux dans l'équation, on obtient :
Vrai ET Vrai = Q
Q = Vrai
Puisque A et B sont tous deux vrais, alors Q doit être vrai.
Il est temps de faire du jus d'orange !
Comment un ordinateur décide quand il peut faire du jus d'orange
|
Condition A (Il y a des oranges dans votre réfrigérateur) |
Condition B (Vous avez un presse-orange) |
Résultat Q (Vous pouvez faire du jus d'orange) |
| Faux | Faux | Faux |
| Faux | Vrai | Faux |
| Vrai | Faux | Faux |
| Vrai | Vrai | Vrai |
Découvrez les portes logiques
De nombreux circuits de votre ordinateur sont des versions physiques d'équations logiques, complétées par des circuits plus petits appelés portes logiques, qui sont des opérateurs logiques physiques.
Une porte logique prend des uns et des zéros (représentant respectivement vrai et faux) en entrée, puis renvoie un 1 ou un 0 en fonction du résultat de l'équation qu'elle contient.
Vous aussi, vous pouvez réaliser des projets vraiment géniaux avec des portes logiques !
Je me souviens de la première fois où mon père m'a parlé des portes logiques : je suis allé directement dans ma chambre et j'ai passé des heures à essayer de les combiner sur papier de différentes manières pour additionner des nombres binaires.
J'espère que vous vous amuserez autant que moi avec elles !
Voyons maintenant comment
fonctionnent quelques portes logiques différentes.
Les portes AND (ET)
vérifient la présence de deux entrées vraies.
La porte AND est la forme physique de l'opérateur ET que vous avez utilisé pour déterminer si vous pouviez faire du jus d'orange.
Une porte AND possède deux entrées ou plus (A et B, par exemple) et une sortie (Q, par exemple).
Elle vérifie si A et B sont toutes les deux à 1.
Si c'est le cas, alors Q est à 1 ; sinon, la sortie est à 0.
Q est à 1 uniquement si A et B
sont toutes les deux à 1 ; si une ou les deux entrées sont à 0, la sortie est à
0.
Je trouve utile d'écrire les valeurs de Q résultant de différentes
combinaisons d'entrées dans une table de vérité.
Cette table de vérité présente toutes les combinaisons d'entrée possibles pour la porte AND et leur sortie. Dans une table de vérité, 0 signifie faux et 1 signifie vrai.

Les portes OR (OU) vérifient la présence d'une seule entrée vraie
La porte OR vérifie si l'entrée A ou B est à 1.
Si l'une ou les deux sont à 1, la sortie Q est également à 1.
En revanche, si les deux entrées sont à 0, la sortie est à 0.

Portes NOT (NON) inverseuses
La porte NOT , aussi appelée inverseur, ne possède qu'une entrée et une sortie, et son fonctionnement est très simple :
la sortie est l'inverse de l'entrée.
Si l'entrée est à 1, la sortie est à 0.
Si l'entrée est à 0, la sortie est à 1.

Une porte AND plus grande
Les portes AND et OR peuvent avoir plus de deux entrées.
Par exemple, voici un symbole de porte AND à 4 entrées :

Comme il s'agit d'une porte AND , le résultat sera 1 seulement si les quatre entrées sont à 1 ; sinon, il sera 0.
Autrement dit, la sortie Q est vraie (1) si les quatre entrées (A, B, C et D) sont vraies (1) :
Q = A AND B AND C AND D
Nous pouvons également réaliser une porte AND à 4 entrées à partir de trois portes AND à 2 entrées, comme ceci :

Comment dessiner des schémas de circuits logiques
Vous pouvez utiliser des portes logiques pour construire un circuit qui vérifie des conditions et décide de l'action à entreprendre en fonction de celles-ci.
Par exemple, imaginez que vous puissiez désactiver votre système d'alarme de la section Qu'est-ce que l'électricité ? en saisissant un code secret.
Vous pourriez ensuite laisser l'alarme activée pendant votre absence ; si quelqu'un ouvrait la porte, il devrait connaître le bon code pour désactiver l'alarme. Grâce aux portes logiques, un circuit peut facilement vérifier si le bon code a été saisi.
Voir Aussi : Les portes Logiques
Dans la section Les portes Logiques on retrouve
Les tables de vérité des Portes Logiques : Portes Logiques Table de Vérité
Faire des portes logiques avec des résistances et des diodes : Logique diode-résistance (DRL)
Faire des portes logiques avec des résistances et des transistor: Logique Résistance-transistor (RTL)
Équation logique pour un code secret
Supposons que le code secret soit 1001, et que lorsqu'il est détecté, une LED s'allume pour indiquer la réussite.
Lors de la construction de circuits logiques, il est utile d'écrire l'équation logique de votre circuit avant de le construire ; alors, entraînons-nous.
Tout d'abord, réfléchissez à la signification de chaque 1 et de chaque 0 du code secret en termes de portes logiques.
Dans ce cas, la LED doit
s'allumer uniquement lorsque quatre conditions sont remplies, et vous pouvez
relier ces conditions à l'aide d'opérateurs AND comme suit :
Représentons
les quatre bits du code secret par les lettres W, X, Y et Z.
Ensuite, vous pouvez vérifier
la valeur de chaque bit pour voir si W = 1, X = 0, Y = 0 et Z = 1.
Vous
devrez relier les quatre bits du code secret par un
AND à l'aide d'une porte
AND à quatre entrées.
En connectant simplement W, X, Y et Z directement à la porte AND , vous obtiendrez l'équation logique suivante :
Q = W AND X AND Y AND Z
Cela permettrait de vérifier si tous les bits sont à 1, car Q = 1 seulement si W, X, Y et Z sont tous à 1.
Il faut plutôt tester le code secret où W et Z sont à 1, mais X et Y sont à 0.
Heureusement, en logique booléenne, vous n'avez que deux options : 1 ou 0 (vrai ou faux).
Si une valeur est 0, alors elle n'est PAS 1 ; autrement dit, si une valeur est fausse, alors elle n'est PAS vraie.
Cela signifie que si X = 0 (faux), alors PAS X = 1 (vrai).
Sachant cela, vous pouvez réécrire l'équation comme suit :
Q = W AND (NOT X) AND (NOT Y) AND Z
Cette équation utilise NON sur les bits X et Y, qui devraient être à 0 pour le code secret.
NOT inverse leurs valeurs, transformant 0 en 1 et 1 en 0.
Conversion d'une équation logique en schéma de circuit
Nous allons maintenant dessiner l'équation du code secret sous forme de circuit.
La sortie finale sera un simple 1 ou 0.
Vous aurez besoin d'une porte AND à 4 entrées pour tester simultanément les quatre bits du code, et vous utiliserez trois portes AND à 2 entrées, comme expliqué précédemment.
Comme vous devez tester si les bits X et Y sont à 0.
Vous devrez utiliser une porte NOT pour chaque bit afin d'inverser le 0 en 1.
Voici le circuit final:
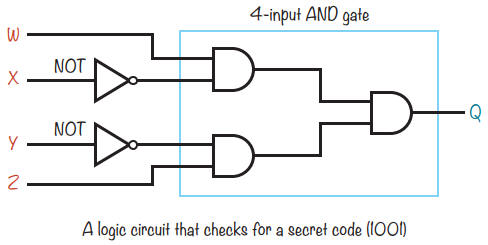
Le premier bit (W) doit être à 1 et le deuxième (X) à 0.
Le deuxième bit reçoit donc une porte NOT.
Le troisième bit (Y) possède également une porte NOT et passe par une porte AND avec le quatrième bit (Z).
La première porte AND doit renvoyer 1 si W = 1 et X = 0, et la deuxième porte AND doit renvoyer 1 si Y = 0 et Z = 1.
Si ces deux portes
AND renvoient 1, la troisième porte ET en fera autant, confirmant ainsi
la saisie de 1001.
Exercice : Dessiner des énoncés plus logiques sous
forme de circuits
Maintenant que vous avez vu les bases, transformez quelques énoncés logiques en circuits logiques sur papier.
Par exemple, comment pourriez-vous élaborer des plans pour un décideur du type « Puis-je faire du jus d'orange ?» ?
Créez-en un en vous basant sur
les énoncés de la section « C'est uniquement logique ».
Utilisation
des portes logiques dans la vie réelle
Quand j'ai découvert les portes logiques, je pensais qu'il s'agirait de petits composants à deux ou trois pattes.
Or, les portes logiques sont intégrées à des circuits intégrés (CI, IC).
Chaque IC contient plusieurs portes ; même si vous ne souhaitez en utiliser qu'une, vous devrez de toute façon utiliser un IC.
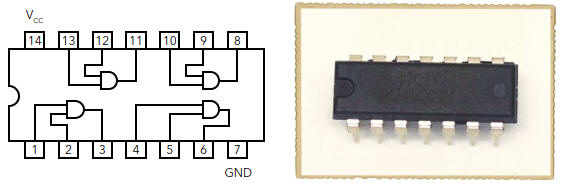
Il est également important de savoir que les sorties des portes logiques ne fournissent pas beaucoup de courant.
Même si une porte logique
fournit 5 V, cela ne signifie pas que vous pouvez y connecter votre moteur 5 V.
La porte logique ne peut tout simplement pas fournir suffisamment de courant
pour faire fonctionner le moteur.
Rappelez-vous, à la section
Contrôler les choses avec
l'électricité, qu'un transistor n'a besoin que d'un faible courant circulant
dans sa base pour devenir passant et qu'un courant beaucoup plus important
circule de son collecteur à son émetteur.
Pour utiliser une porte logique pour activer un circuit ou un composant nécessitant plus de courant, vous pouvez connecter la porte logique à un transistor.
Vous souvenez-vous du circuit
du « Projet n° 14 : Construire un circuit tactile » section
Contrôler les choses avec
l'électricité ?
Vous pouvez modifier ce circuit pour allumer
une LED à partir d'une porte logique, comme ceci :
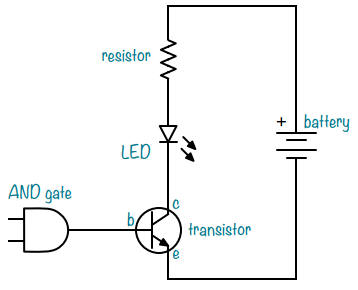
Je vous montrerai comment intégrer cela dans un projet dans la section suivante.
En savoir plus sur le courant, les composants et les transistors
Vous pouvez facilement remplacer la LED et la résistance par un autre élément à contrôler, comme un moteur, un ventilateur ou un relais.
Mais attention au courant.
De quel courant votre moteur
a-t-il besoin et quel courant le transistor peut-il supporter ?
Ces deux
valeurs sont indiquées dans les fiches techniques des composants.
Pour les transistors, la valeur recherchée est appelée courant de collecteur (IC).
Selon la fiche technique d'un
transistor BC547, son courant de collecteur maximal est de 100 mA. C'est
largement suffisant pour alimenter une LED, qui consomme généralement entre 15
et 20 mA maximum.
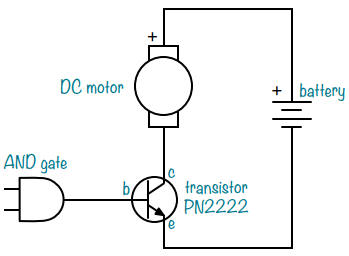
Et si vous souhaitez connecter un moteur ?
Vous devez d'abord déterminer le courant nécessaire au moteur, que vous trouverez dans sa fiche technique.
Si un moteur a besoin de 500 mA, vous devrez le connecter à un transistor capable de supporter un courant supérieur à 500 mA.
Par exemple, un transistor PN2222 peut gérer jusqu'à 600 mA, il devrait donc pouvoir allumer et éteindre le moteur.
Projet n° 21 : Un vérificateur de code secret
Dans ce projet, vous construirez un circuit logique qui vérifie si un ensemble de quatre bits d'entrée correspond à un code secret.
Vous utiliserez quatre commutateurs, à l'intérieur d'un commutateur DIP, pour définir le code.
Si les bits d'entrée correspondent au code, le circuit logique doit fournir une tension, représentant 1 ; sinon, il doit fournir une tension nulle, indiquant 0.
Cette sortie finale sera envoyée à un transistor, ce qui vous permettra de contrôler quelque chose, comme une alarme !
Le circuit de base du vérificateur de code secret allume une LED lorsque vous saisissez le bon code.
À la fin du projet, je vous montrerai comment utiliser le vérificateur de code secret pour désactiver votre alarme anti-intrusion, comme expliqué à la section Qu'est-ce que l'électricité ?.
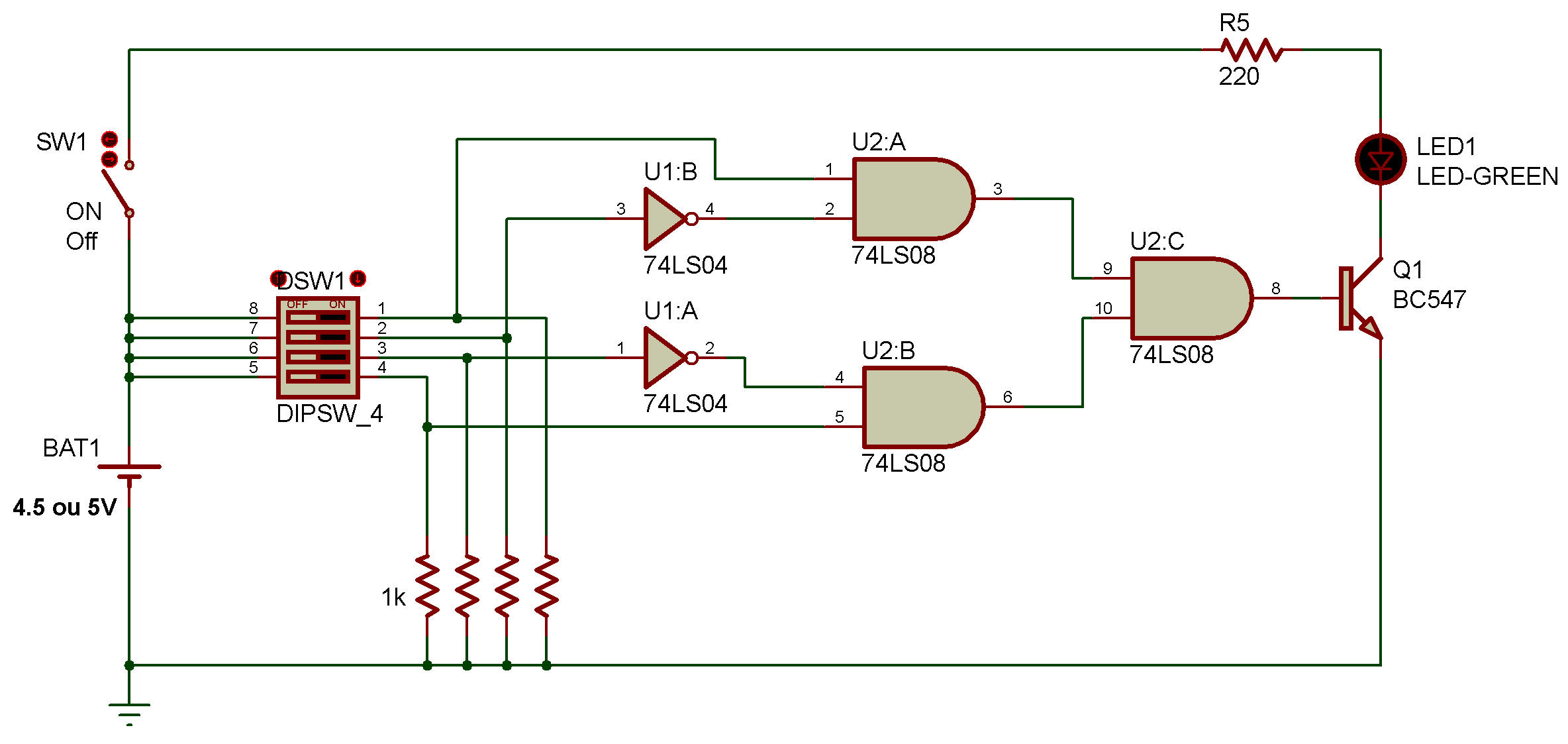
Voici le schéma de circuit complet pour ce projet :
Liste de courses voir Fournitures utiles
Une Breadboard (platine d'expérimentation) avec au moins 60 rangées (Full).
Fils de liaison pour Breadboard.
Un commutateur DIP avec quatre commutateurs.
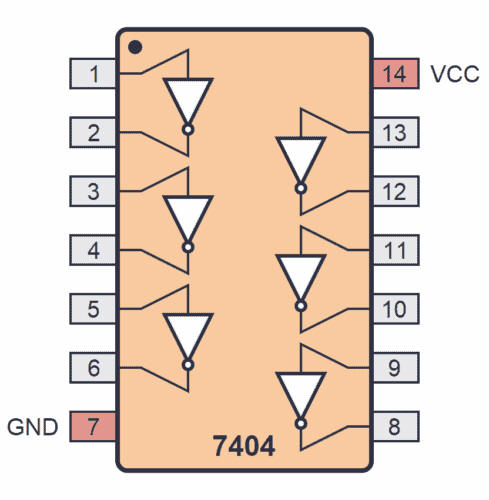
Un circuit intégré inverseur 74LS04 avec six portes NOT.
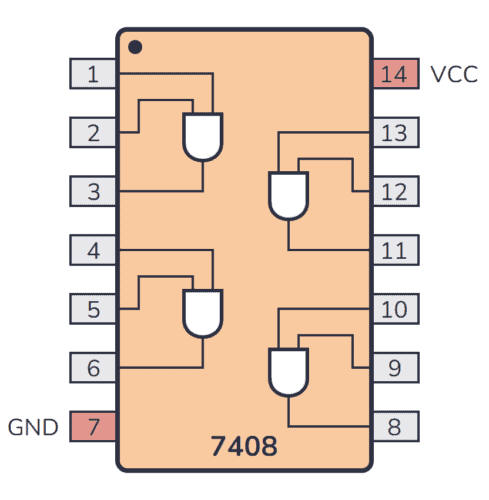
Un circuit intégré 74LS08 avec quatre portes AND.
AVERTISSEMENT
La tension d'alimentation CC (Vcc) de la série 74XX Famille TTL doit être fournie dans la limite de +4,5 Volts à +5,25 Volts.
Ne pas dépasser ce voltage sinon le IC pourrait sauter.
Fournitures utiles pour plus de détail.
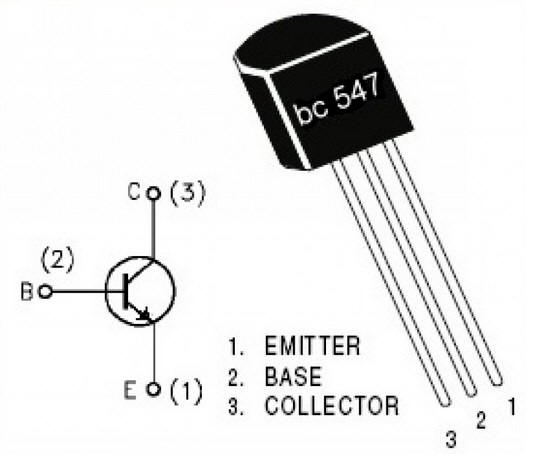
Un transistor NPN à usage général, tel que le BC547.
Une LED standard.
Une résistance de 220 Ω pour limiter le courant de la LED.
Quatre résistances de 1 kΩ pour les résistances de rappel vers le bas.
Un adaptateur secteur 5 V CC pour alimenter le circuit.

Un adaptateur jack cylindrique CC pour connecter l'adaptateur secteur à la platine de lecture.

ou
Un Supports de piles AA 4.5V (3 x AA) avec interrupteur et couvercle

Voir Fournitures utiles pour d'autre option d'alimentation
Outils
Un tournevis qui s'adapte à la borne à vis de l'adaptateur de prise jack cylindrique. Si vous en utilisez un.
Comment utiliser d'autres tensions avec une platine d'expérimentation
Vous avez déjà utilisé des piles de 9 V pour chaque circuit de Mes premiers pas en Électronique, mais la plupart des circuits numériques nécessitent des tensions plus faibles.
Par exemple, de nombreux circuits intégrés avec portes logiques utilisent 5 V.
Cependant, 5 V n'est pas une valeur standard pour les piles ; il existe des piles de 4,5 V et 6 V, mais pas de 5 V.
Que faire lorsque votre circuit nécessite 5 V ?
N'hésitez pas à utiliser l'adaptateur secteur et l'adaptateur jack cylindrique.

De nombreux appareils électroniques utilisent des adaptateurs muraux pour recharger leurs batteries ou simplement pour rester alimentés.
Le côté à broches d'un adaptateur mural se branche sur une prise murale, tandis que l'autre côté se branche sur un appareil à alimenter.
Les adaptateurs muraux sont disponibles en plusieurs tensions, et ce projet utilise un adaptateur régulé 5 V CC.
Pour alimenter un circuit, l'adaptateur mural de ce projet doit être branché sur un adaptateur jack cylindrique.
L'adaptateur jack cylindrique mentionné dans la liste d'achats de ce projet possède deux bornes à vis permettant de brancher des fils de liaison à la platine d'expérimentation.
Vous pouvez connecter n'importe quel adaptateur mural doté d'une fiche ronde standard à cet adaptateur jack cylindrique.
Fiabilisation des circuits
Si un circuit nécessite une tension d'entrée et que vous ne connectez pas cette entrée à quoi que ce soit, cette entrée est flottante.
Une entrée flottante est peu fiable, car le circuit peut la percevoir comme un 1 ou un 0, sans que vous puissiez contrôler lequel.
Les commutateurs d'un commutateur DIP sont soit ouverts, soit fermés.
Lorsque le commutateur est ouvert, l'entrée qu'il contrôle est flottante si elle n'est connectée à rien d'autre.
Pour résoudre ce problème, vous pouvez connecter une résistance de rappel (pull-down resistor) à chaque entrée des portes logiques, comme ceci :
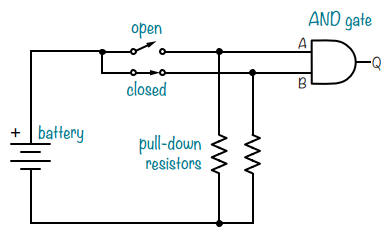
Chaque résistance de rappel à la terre de ce schéma est connectée à un interrupteur et à une entrée de grille d'un côté,
et à la borne négative de la batterie de l'autre.
Lorsqu'un interrupteur est ouvert, la résistance ramène l'entrée de grille à 0 V, soit 0.
Lorsqu'un interrupteur est fermé, l'entrée de grille est connectée à la borne positive et reçoit la tension d'alimentation positive, soit 1.
Dans le schéma de ce projet, on trouve quatre interrupteurs avec des résistances de rappel à la terre de 1 kΩ. Ils sont tous représentés ouverts, et toutes les entrées de la porte ET seraient alors à 0.
Étape 1 : Placer les interrupteurs et les résistances
Branchez votre interrupteur DIP à gauche de la plaque d'essai, en plaçant un côté de l'interrupteur de chaque côté de l'encoche centrale.
Utilisez des cavaliers pour relier le côté gauche de chaque interrupteur DIP au rail d'alimentation positif, et connectez une résistance de 1 kΩ du côté haut de chaque interrupteur DIP au rail d'alimentation négatif.

Étape 2 : Placer les circuits intégrés
Placez le circuit intégré avec portes NON, marqué 74LS04, au milieu de la plaque d'essai et le circuit intégré avec portes ET, marqué 74LS08, plus bas.
Pour les deux circuits intégrés, orientez l'encoche arrondie vers la gauche.
Connectez les fils de liaison de la broche 14 des deux circuits intégrés au rail d'alimentation positif et de la broche 7 des deux puces au rail d'alimentation négatif.
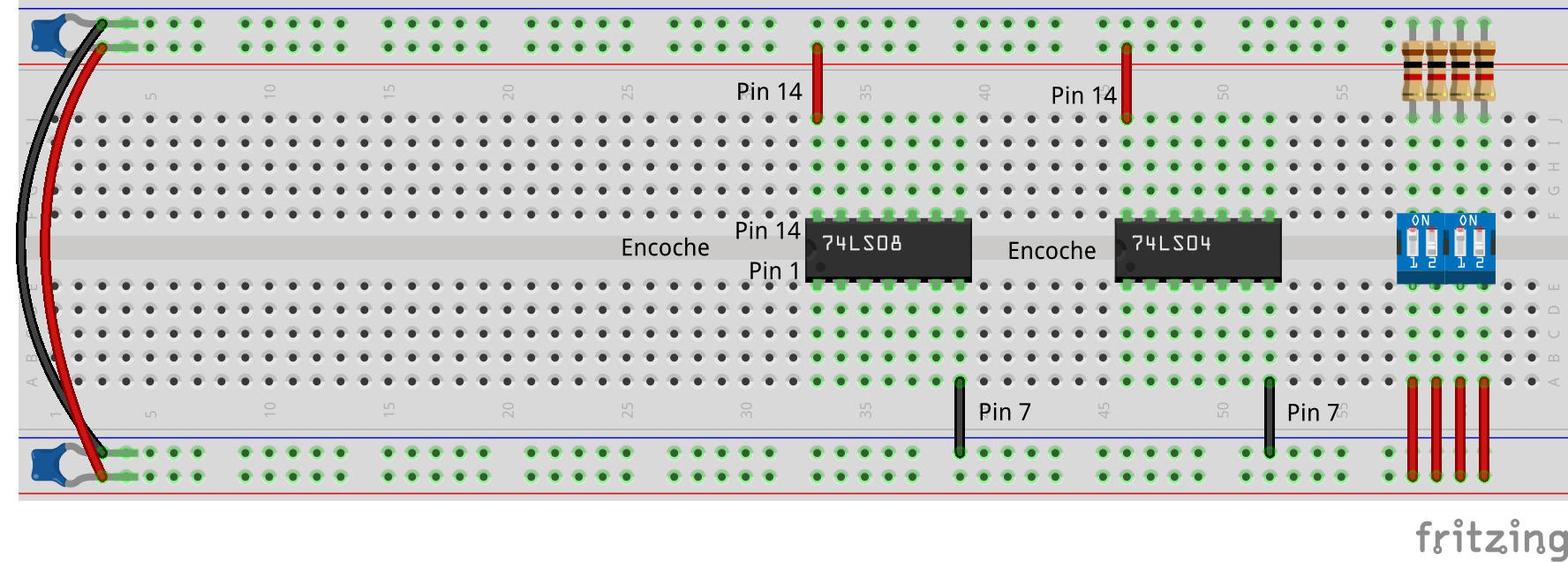
Étape 3 : Placer le transistor et la LED
Branchez votre transistor sur les trois rangées supérieur de la plaque d'essai.
Si vous avez utilisé le transistor BC547 de la liste d'achats de ce projet, orientez le côté plat de sorte que le collecteur soit la broche gauche, la base la broche centrale et l'émetteur la broche droite.
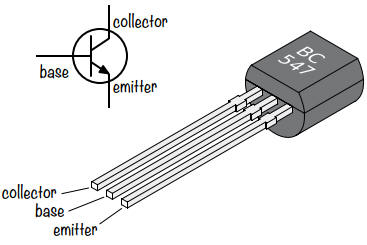
Si vous avez utilisé un autre transistor NPN, consultez sa fiche technique pour identifier la broche correspondante.
Connectez la patte courte de la LED (la cathode) à la même rangée que le collecteur.
Connectez la patte longue de la LED (l'anode) à une rangée libre du côté gauche de la plaque d'essai.
Enfin, connectez la résistance de 220 Ω reliant l'anode de la LED au pôle positif de l'alimentation.
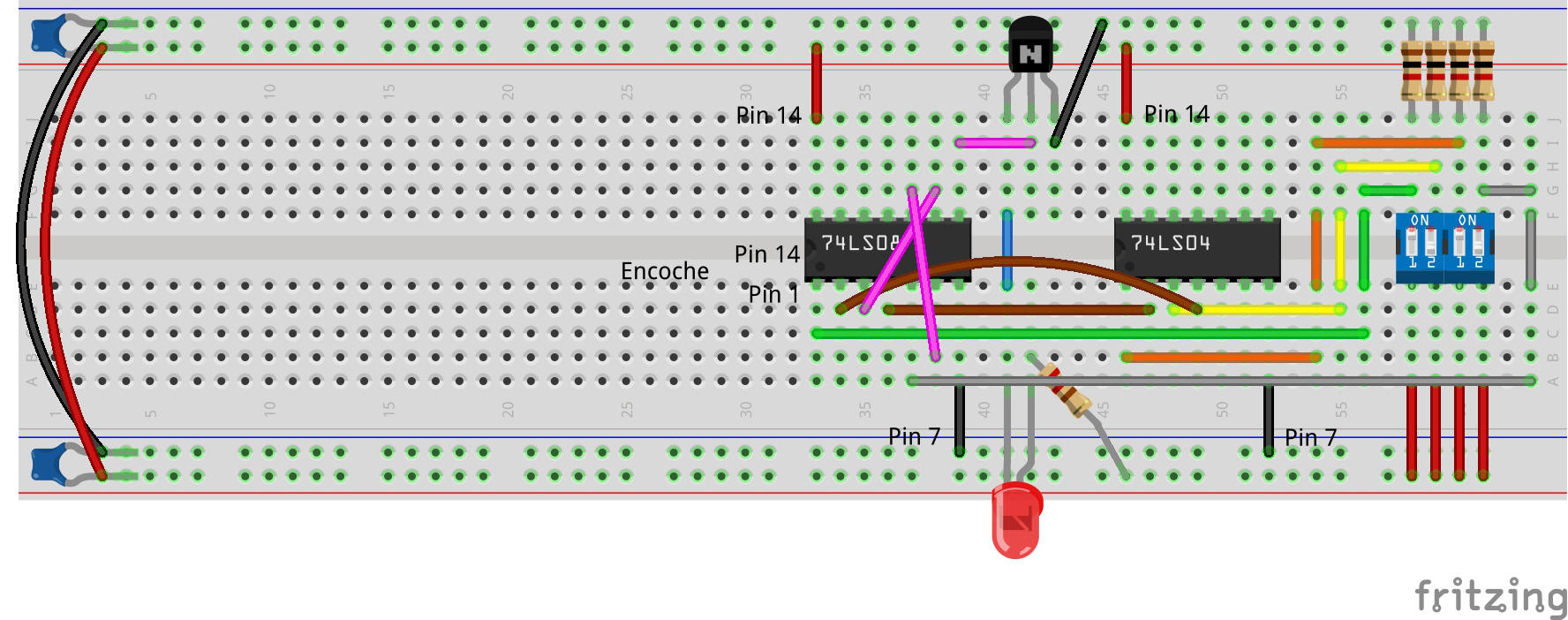
Étape 4 : Construire le circuit logique
Tout d’abord, observez le schéma suivant pour identifier l’emplacement des portes AND et NOT dans vos circuits intégrés et les connexions à réaliser.


Prenez quatre fils de liaison et connectez-les des sorties du commutateur aux entrées de la porte comme suit :
La sortie du commutateur 1, est reliée à l'entrée de la porte AND sur la broche 1 du circuit intégré (74LS08). Fils Verts.
La sortie du commutateur 2 est reliée à l'entrée de la porte NOT sur la broche 3 du circuit intégré (74LS04). Fils Janes
La sortie du commutateur 3 est reliée à l'entrée de la porte NOT sur la broche 1 du circuit intégré (74LS04). Fils Oranges
La sortie du commutateur 4 va à l'entrée de la porte AND sur la broche 5 du circuit intégré (74LS08) Fils Gris
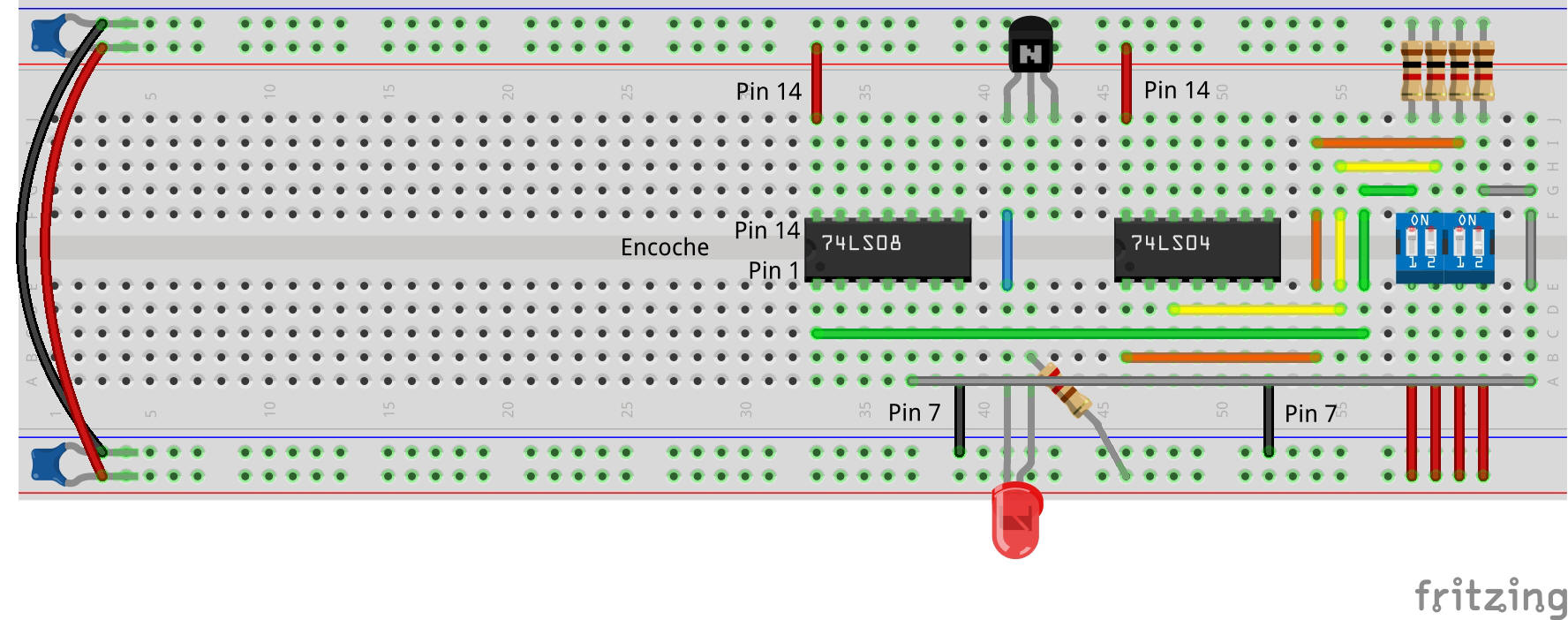
Ensuite, utilisez deux fils de liaison pour connecter les sorties des portes NON aux entrées des portes ET, comme suit :
Un fil de liaison relie la broche 4 du 74LS04 à la broche 2 74LS08. Brun
L'autre fil de liaison relie la broche 2 du 74LS04 à la broche 4 du 74LS08. Fils
Chaque sortie des portes AND doit être connectée à la troisième porte AND, comme suit :
Connectez un fil de liaison de la broche 3 à la broche 9 du circuit intégré 74LS08. Fils Rose
Connectez un autre fil de liaison de la broche 6 à la broche 10 du circuit intégré 74LS08.
Enfin, connectez un fil de liaison à la dernière sortie de la porte AND 74LS08, broche 8 à la base du transistor.
Cette sortie contrôlera si le transistor laisse passer le courant vers la LED.
Connectez un cavalier entre l'émetteur du transistor et le pôle négatif de l'alimentation.
Protection des composants
Le circuit de ce projet repose sur le fait que les portes ne fournissent qu'une faible quantité de courant à la base du transistor.
Votre transistor fonctionnera parfaitement pendant l'utilisation de votre vérificateur de code secret, mais pour protéger sa base des dommages causés par des courants plus importants dans d'autres circuits, vous devez placer une résistance d'environ 1 à 10 kΩ entre la base du transistor et sa source de courant – dans ce cas, la sortie de la porte ET.
Les transistors doivent également être généralement protégés dans les circuits moteurs, comme celui décrit dans « En savoir plus sur le courant, les composants et les transistors .
Ce circuit devrait fonctionner
tel quel, mais par mesure de précaution, il est conseillé de connecter une diode
aux bornes du moteur, la cathode étant du côté positif. Cela devrait protéger le
transistor des pics de tension pouvant survenir lorsque le moteur est éteint.
Étape 6 : Alimenter et tester le vérificateur de code secret
Désactivez tous les interrupteurs du commutateur DIP et connectez votre source 5 V, le plus à l'alimentation positive et le moins à l'alimentation négative.
Utilisez votre adaptateur jack cylindrique avec quelques fils de liaison pour réaliser cette connexion.
L'adaptateur jack cylindrique doit comporter des repères + et – pour indiquer l'alimentation. Desserrez simplement les vis de l'adaptateur, insérez un fil dans chaque connecteur, puis resserrez les vis.

Suivez le code couleur habituel : utilisez un fil rouge pour le positif et un fil noir pour le négatif afin de vous assurer de les connecter correctement sur votre platine d'expérimentation.
La LED doit rester éteinte lorsque les interrupteurs sont désactivés, mais lorsque vous réglez le code sur 1001 en activant les interrupteurs du haut et du bas, elle doit s'allumer.
Étape 7 : Que faire si la LED ne s’allume pas ?
Vérifiez d’abord que les deux circuits intégrés sont alimentés. La broche 14 est-elle connectée à la borne positive et la broche 7 à la borne négative ?
Si les circuits intégrés deviennent trop chauds au toucher, débranchez immédiatement l’alimentation 5 V et attendez qu’ils refroidissent.
Vérifiez ensuite le bon sens des connexions d’alimentation avant de réessayer. Le fil branché à la borne positive (+) de l’adaptateur jack doit être branché à la borne positive de la platine d’expérimentation, et le fil branché à la borne négative (–) de l’adaptateur jack doit être branché à la borne négative.
Si les circuits intégrés sont alimentés et que le circuit ne fonctionne toujours pas, vérifiez les valeurs d’entrée des commutateurs.
À l’aide d’un multimètre, mesurez la tension entre le rail d’alimentation négatif et les broches des portes AND et NOT qui reçoivent les entrées des commutateurs.
Vous devriez obtenir 5 V sur les broches 1 et 13 du circuit intégré AND et 0 V sur les broches 11 et 13 du circuit intégré NON.
Vérifiez que la sortie de chaque porte AND utilisée est également de 5 V ; vous devriez voir 5 V sur les broches 3, 8 et 11.
Si une porte ET du circuit intégré ne produit pas 5 V, l'une de ses entrées est à 0 V. Trouvez la raison de ce 0 V et vous devriez trouver le problème.
Essayez : Désarmez votre alarme anti-intrusion
Au lieu d'une LED et d'une résistance, vous pouvez connecter un relais au vérificateur de code secret et combiner ce projet avec l'alarme anti-intrusion que vous avez construite à la section Qu'est-ce que l'électricité ?.
Connectez la pile 9 V à l'alarme anti-intrusion via le relais.
Ainsi, lorsque vous saisissez le bon code, l'alimentation de l'alarme est coupée et le bruit s'arrête. Reportez-vous à la section « Découvrez le relais » pour savoir comment connecter un relais.
Notez que le vérificateur de code secret, avec son alimentation 5 V, sert à contrôler le circuit d'alarme anti-intrusion entièrement séparé de l'alimentation 9 V.
Connecter ainsi deux circuits avec des alimentations séparées est possible, car il n'y a aucune connexion électrique entre les deux circuits.
Les relais sont utiles pour contrôler un circuit avec un type d'alimentation différent !
Voici le circuit :
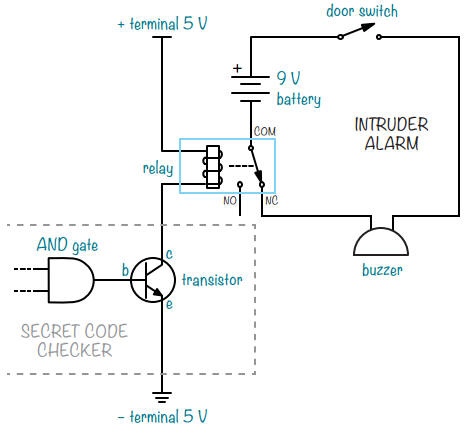
Voici les composants dont vous
aurez besoin :
Le circuit du « Projet n° 2 : Alarme anti-intrusion »
Le circuit du « Projet n° 21 : Vérificateur de code secret »
Un relais 5 V
Si vous prévoyez souder votre projet il existe des plaque à souder qui sont une copie conforme d'un Breadboard. Ce qui facilicite grandement le montage et la soudure.

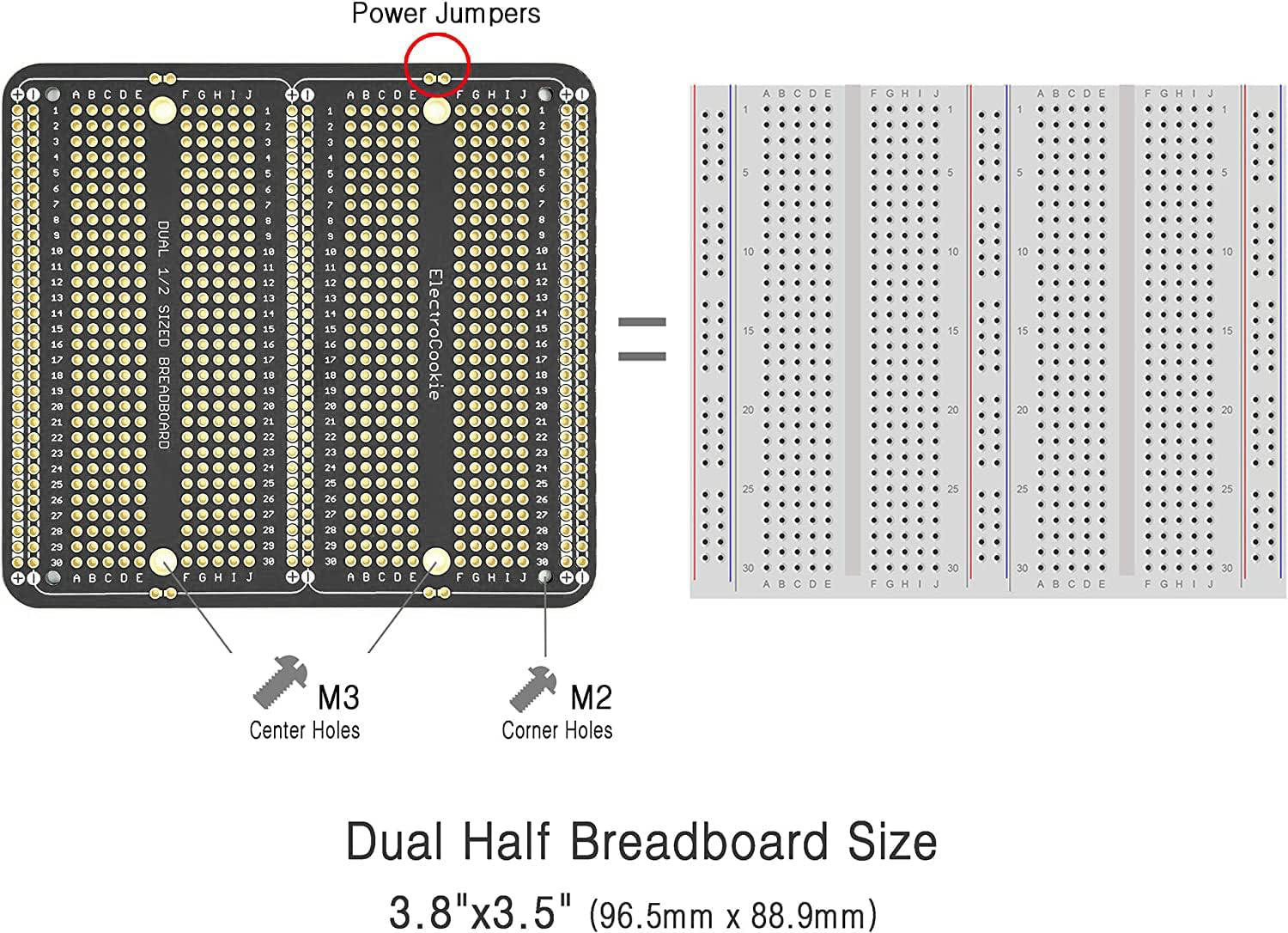
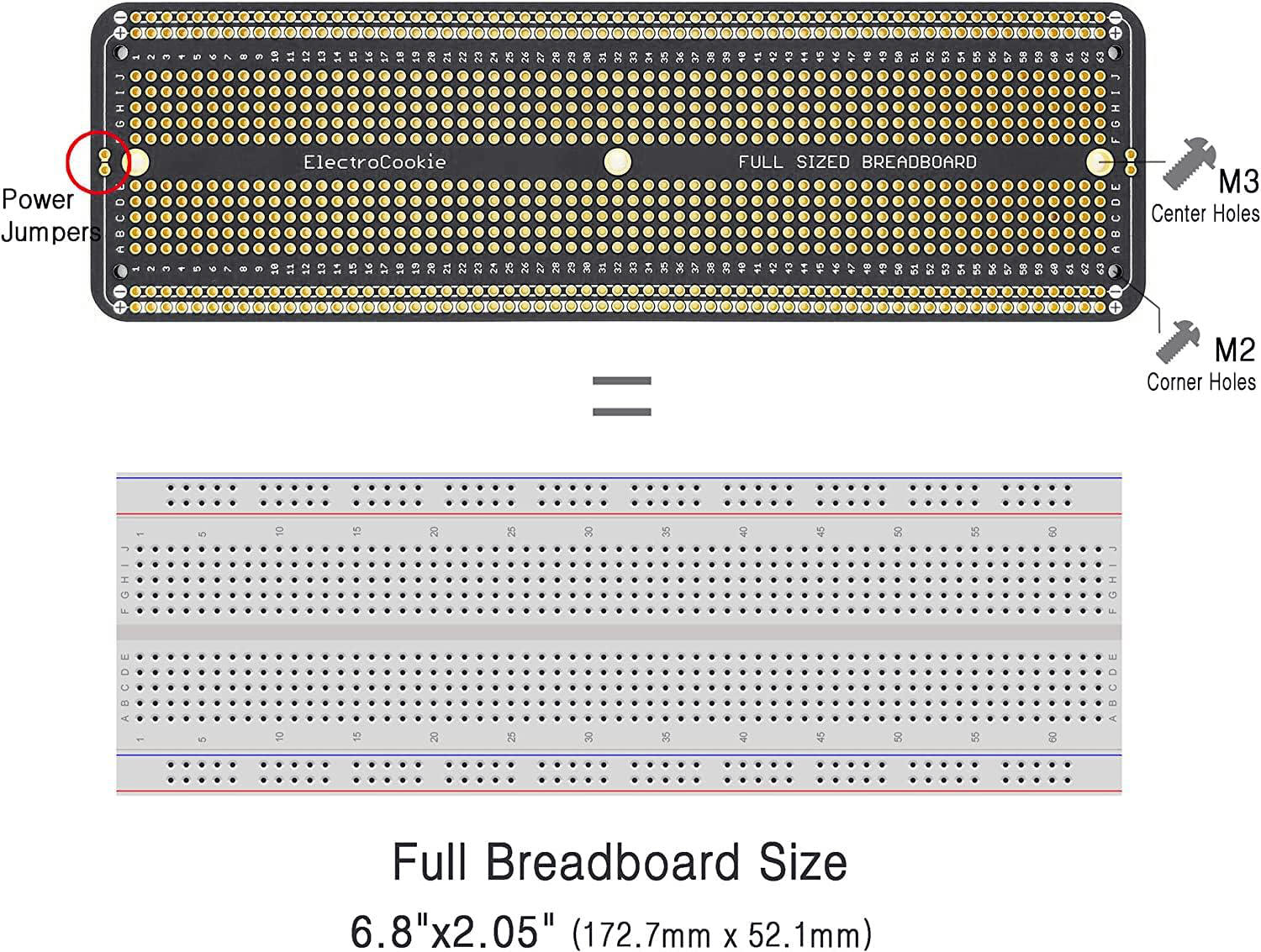
Et vous pouvez souder des prises à transistor et à IC ou lieu de souder directement ces composantes.
Prise pour transistor (Transistor Sockets)

Prises pour circuit intégré (IC Sockets)

Portes logiques négatives
Les portes AND, OR et NOT sont des portes logiques de base, et vous pouvez les combiner pour en créer de nouvelles.
Examinons deux autres portes ainsi créées.
La porte NAND recherche une entrée fausse
La porte NAND fonctionne comme une porte ET avec un inverseur de porte NON en sortie.
Le petit cercle sur la sortie signifie NOT. Cela signifie que la sortie de la porte NAND est à 0 lorsque A et B sont tous deux à 1.
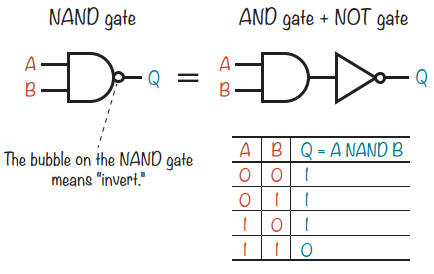
La porte NOR recherche deux entrées fausses.
La porte NOR fonctionne comme une porte OU avec un inverseur en sortie. La sortie est à 1 lorsque A et B sont tous deux à 0.
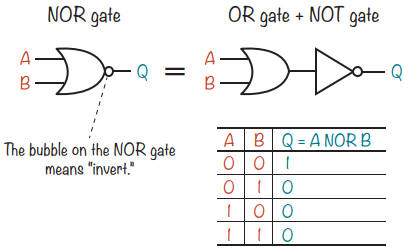
Et ensuite ?
Dans cette section, vous avez appris à utiliser des portes logiques pour construire des circuits qui « déterminent » des choses, comme si un code est correct ou non.
À la fin, vous avez également pu découvrir des portes logiques négatives. Comprendre leur fonctionnement est utile, car elles sont souvent utilisées dans des circuits réels. D'ailleurs, vous les utiliserez à la section suivante:
Des circuits qui mémorisent des informations.
Si vous souhaitez explorer les portes plus en détail, je vous suggère de combiner des portes logiques que vous avez déjà étudiées sur papier pour créer une porte XOR.
Une porte XOR ne donne 1 que si les entrées sont différentes.
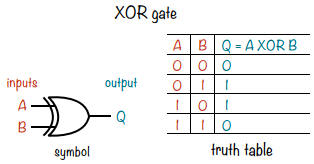
En combinant les portes logiques de différentes manières, vous pouvez créer presque tout ce que vous pouvez imaginer.
Voir : Les portes Logiques
Mais cela peut paraître un peu
difficile à imaginer pour l'instant ; c'est pourquoi, dans le prochain section,
je vais vous montrer d'autres blocs de construction que vous pouvez créer avec
des portes logiques.
Vous apprendrez à construire votre propre circuit
mémoire, puis votre propre pile ou face électronique !