Aide-mémoire sur les composants
Mes premiers pas en Électronique
Tout au long de cette section, vous utiliserez de nombreux composants, et il existe autant de façons de les interpréter que de types de composants. Voici quelques aide-mémoire pratiques pour vous aider à interpréter les résistances et les condensateurs, et à mémoriser la signification des différents préfixes d'unités comme les volts et les ampères.
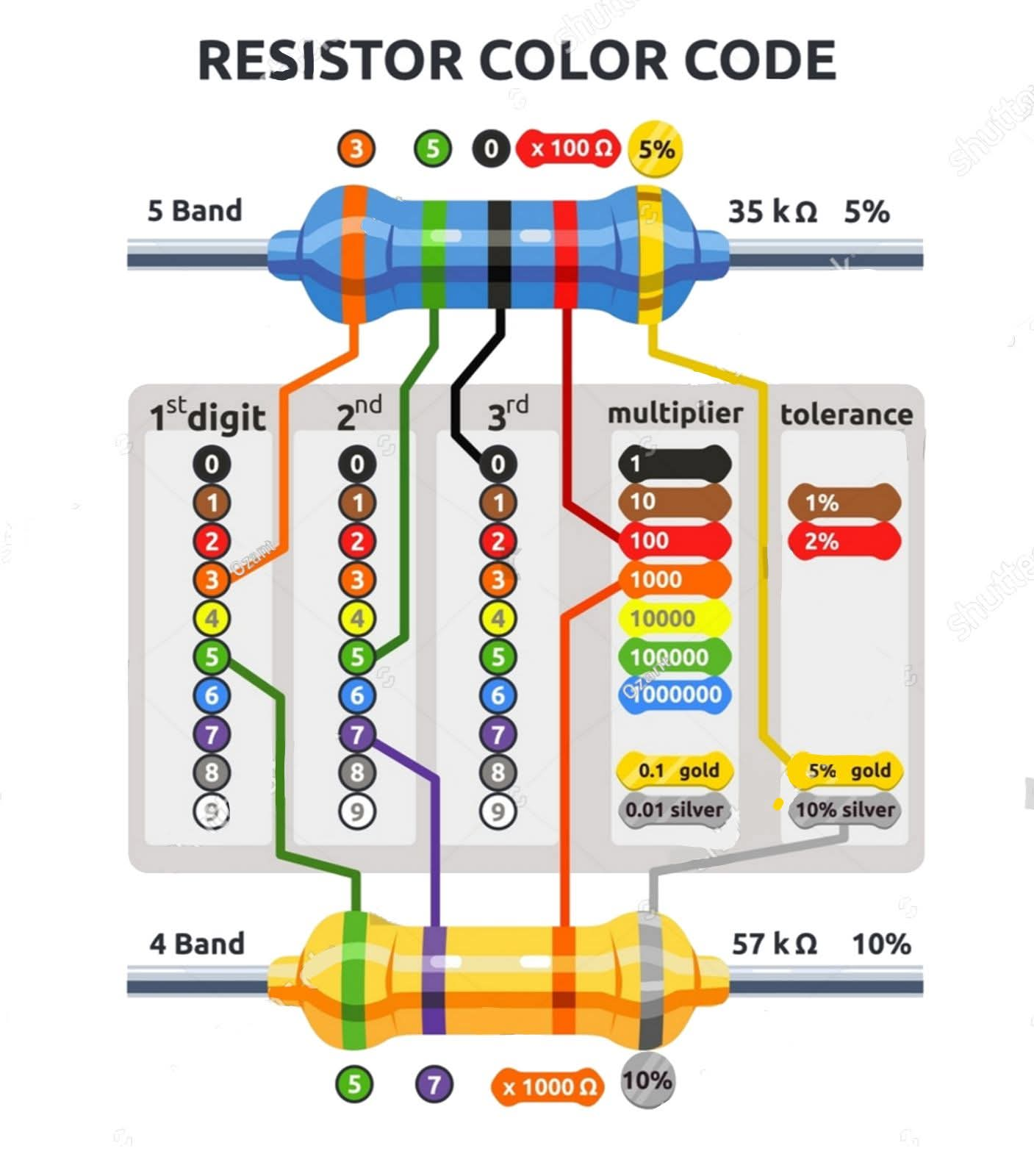
Codes couleur des résistances
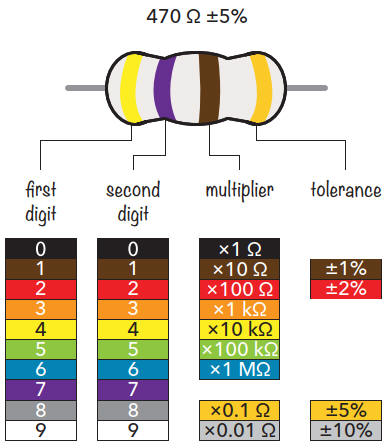
La plupart des résistances présentées dans cette section ont quatre bandes de couleur. Pour déterminer la valeur d'une résistance, il suffit de rechercher ses couleurs sur le schéma suivant et de multiplier en conséquence.
Par exemple, pour obtenir 470 Ω, il faut multiplier le nombre 47 (indiqué par les bandes jaune et violette) par 10 (indiqué par la bande marron).
Pour plus de détails sur les résistances, voir « Découvrez la résistance » à la section Créer de la lumière avec des leds.
Voir aussi : Résistances, Roue de code couleur des résistances

Voici un tableau pour des résistances à 4 ou 5 Bandes
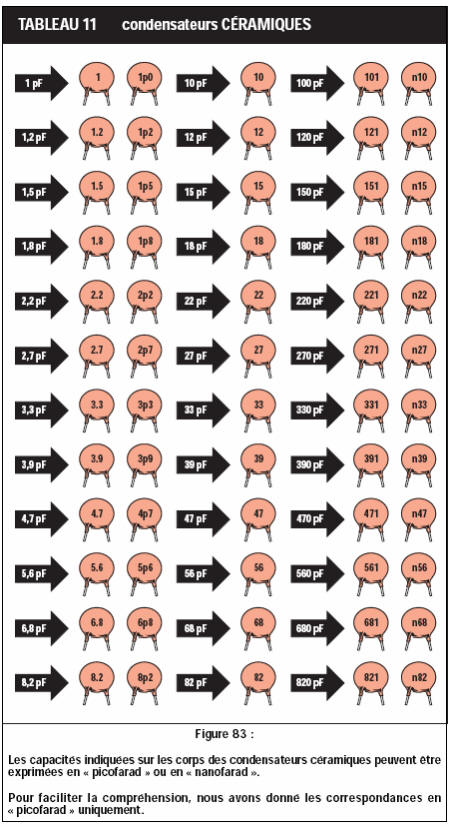
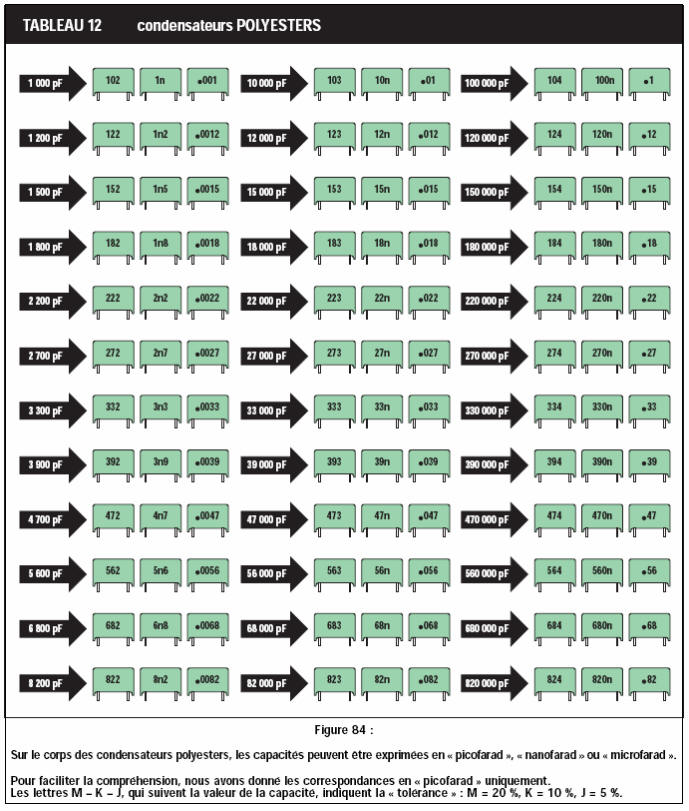
Codes des condensateurs
Le tableau suivant répertorie les codes des condensateurs les plus courants. Consultez-le si vous utilisez des condensateurs céramiques ou au tantale, car, contrairement aux condensateurs électrolytiques utilisés dans la majeure partie de cette section, leur capacité n'est pas indiquée directement.
| Code | Picofarad (pf) | nanofarad (nf) | Microfarad (µf) |
| 101 | 100 | 0.1 | 0.0001 |
| 102 | 1,000 | 1 | 0.001 |
| 103 | 10,000 | 10 | 0.01 |
| 104 | 100,000 | 100 | 0.1 |
| 105 | 1,000,000 | 1,000 | 1 |
Si vous possédez un
condensateur dont le code est différent de ceux indiqués ici, vous pouvez
trouver sa valeur en picofarads en prenant les deux premiers chiffres et en
ajoutant le nombre de zéros du troisième chiffre.
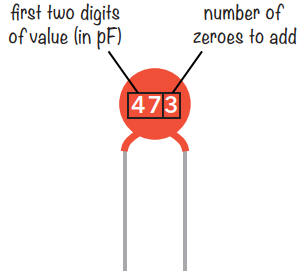
Dans cet exemple, le condensateur porte le code 473.
Prenez les deux premiers chiffres, 47, et ajoutez le nombre de zéros spécifié par le troisième chiffre, 3. Cela vous donne 47 000 pF, soit 47 nF, ou 0,047 µF.
Voir aussi : Condensateurs
| CODE | nF | uF | CODE | nF | uF | |||
| 1N0 | 102 | 1 | 0,001 | 20N | 203 | 20 | 0,02 | |
| 1N1 | 112 | 1,1 | 0,0011 | 22N | 223 | 22 | 0,022 | |
| 1N2 | 122 | 1,2 | 0,0012 | 24N | 243 | 24 | 0,024 | |
| 1N3 | 132 | 1,3 | 0,0013 | 27N | 273 | 27 | 0,027 | |
| 1N5 | 152 | 1,5 | 0,0015 | 30N | 303 | 30 | 0,03 | |
| 1N6 | 162 | 1,6 | 0,0016 | 33N | 333 | 33 | 0,033 | |
| 1N8 | 182 | 1,8 | 0,0018 | 39N | 393 | 39 | 0,039 | |
| 2N0 | 202 | 2 | 0,002 | 47N | 473 | 47 | 0,047 | |
| 2N2 | 222 | 2,2 | 0,0022 | 56N | 563 | 56 | 0,056 | |
| 2N4 | 242 | 2,4 | 0,0024 | 68N | 683 | 68 | 0,068 | |
| 2N7 | 272 | 2,7 | 0,0027 | 82N | 823 | 82 | 0,082 | |
| 3N0 | 302 | 3 | 0,003 | 100N | 104 | 100 | 0,1 | |
| 3N3 | 332 | 3,3 | 0,0033 | 120N | 124 | 120 | 0,12 | |
| 3N6 | 362 | 3,6 | 0,0036 | 150N | 154 | 150 | 0,15 | |
| 3N9 | 392 | 3,9 | 0,0039 | 180N | 184 | 180 | 0,18 | |
| 4N3 | 432 | 4,3 | 0,0043 | 220N | 224 | 220 | 0,22 | |
| 4N7 | 472 | 4,7 | 0,0047 | 270N | 274 | 270 | 0,27 | |
| 5N1 | 512 | 5,1 | 0,0051 | 330N | 334 | 330 | 0,33 | |
| 5N6 | 562 | 5,6 | 0,0056 | 390N | 394 | 390 | 0,39 | |
| 6N2 | 622 | 6,2 | 0,0062 | 470N | 474 | 470 | 0,47 | |
| 6N8 | 682 | 6,8 | 0,0068 | 560N | 564 | 560 | 0,56 | |
| 7N5 | 752 | 7,5 | 0,0075 | 680N | 684 | 680 | 0,68 | |
| 8N2 | 822 | 8,2 | 0,0082 | 820N | 824 | 820 | 0,82 | |
| 9N1 | 912 | 9,1 | 0,0091 | |||||
| 10N | 103 | 10 | 0,01 | CODE | uF | |||
| 11N | 113 | 11 | 0,011 | 1U | 105 | 1 | ||
| 12N | 123 | 12 | 0,012 | 1U2 | 125 | 1,2 | ||
| 13N | 133 | 13 | 0,013 | 1U5 | 155 | 1,5 | ||
| 15N | 153 | 15 | 0,015 | 1U8 | 185 | 1,8 | ||
| 16N | 163 | 16 | 0,016 | 2U8 | 225 | 2,2 | ||
| 18N | 183 | 18 | 0,018 | 4U7 | 475 | 4,7 | ||
Préfixes standards
Lors de la réalisation de projets électroniques, comme dans de nombreux domaines scientifiques, nous sommes parfois confrontés à des nombres très petits ou très grands.
Heureusement, le Système international d'unités (SII) propose des préfixes standards qui facilitent l'écriture de ces nombres.
Ces préfixes sont des multiplicateurs, comme indiqué dans le tableau.
| Préfixe | Nom | Multiplier la valeur par | Exemple d'utilisation |
| p | pico | × 0,000 000 000 001 |
Valeurs des condensateurs (exemple : condensateur de 47 pF) |
| n | nano | × 0,000 000 001 |
Valeurs des condensateurs (exemple : condensateur de 100 nF) |
| µ | micro | × 0,000 001 |
Valeurs des condensateurs (exemple : condensateur de 10 µF) |
| m | milli | × 0,001 |
Courants dans un circuit (exemple : courant de 20 mA) |
| - | - | × 1 | Les tensions n'ont souvent pas de préfixe (exemple : pile de 9 V) |
| K | kilo | × 1,000 |
Valeurs des résistances supérieures à 1 000 (exemple : résistance de 1 kΩ) |
| M | mega | × 1,000,000 |
Taille des fichiers (exemple : photo de 2 Mo) |
| G | giga | × 100,0000,000 |
Taille des fichiers (exemple : vidéo de 1 Go) |
| T | tera | × 1,000,000,000,000 |
Taille des disques durs (exemple : disque dur de 2 To) |
Voir aussi: Table Des Symbole Métrique
Un bref rappel sur la loi d'Ohm
La loi d'Ohm est un élément tellement essentiel du calcul des valeurs dans les circuits que vous y reviendrez sans cesse au fil de vos projets. Pour vous rafraîchir la mémoire sur la détermination de la tension, du courant ou de la résistance dans un circuit, consultez simplement cette section.
V = I × R
La tension V (en volts) est égale au courant I (en ampères) multiplié par la résistance R (en ohms).
I = V / R
Le courant I (en ampères) est égal à la tension V (en volts) divisée par la résistance R (en ohms)
R = V / I
La résistance R (en ohms) est égale à la tension V (en volts) divisée par le courant I (en ampères)
Dans l'équation de la loi d'Ohm, vous devez utiliser les volts (V), les ampères (A) et les ohms (Ω). Pensez donc à convertir les unités si nécessaire :
1 mA = 0,001 A et 1 kΩ = 1 000 Ω.
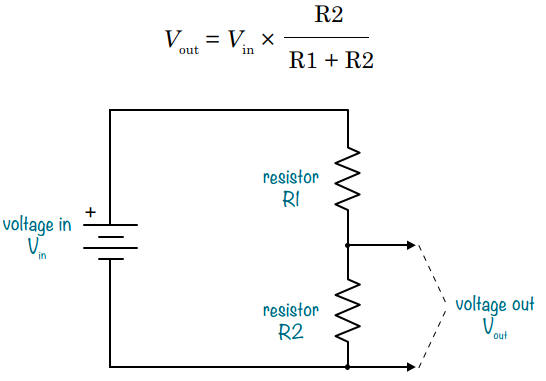
Circuit diviseur de tension basique
Le diviseur de tension est un circuit très utile, par exemple, lorsque vous disposez d'un capteur à résistance, comme une thermistance qui mesure la température, ou une photorésistance qui détecte la lumière.
Voir « Projet No. 15 Construire un réveil à l'aube » à la section Contrôler les choses avec l'électricité pour un projet utilisant un diviseur de tension comme celui-ci.
Vous pouvez également utiliser vos connaissances sur le diviseur de tension pour calculer les tensions dans un circuit afin de comprendre ce qui se passe.
Lorsque vous avez deux résistances en série, elles forment un diviseur de tension. La tension d'entrée est divisée entre les deux résistances, et la tension de sortie (aux bornes de R2) est donnée par la formule :