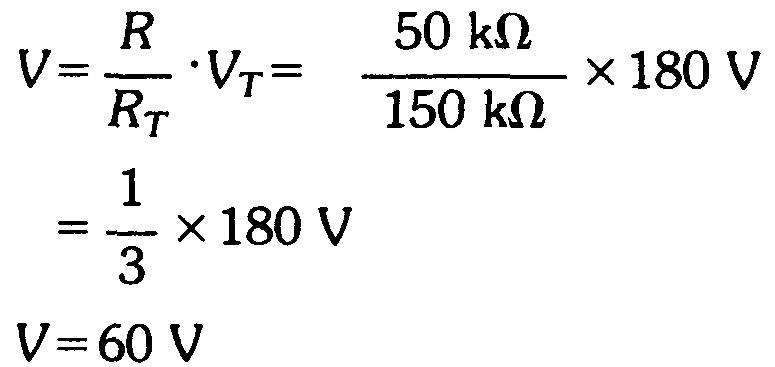
Chapitre 6 - Diviseurs de tension et diviseurs de courant
Mon premier cours en électronique
Tout circuit série est un diviseur de tension.
Les chutes de tension IR sont des portions proportionnelles de la tension appliquée.
De la même façon, tout circuit parallèle est un diviseur de courant. Le courant de chaque branche ou courant dérivé est une fraction du courant d'alimentation total, il est inversement proportionnel à la résistance de la branche considérée.
On peut, pour abréger les calculs, utiliser les formules de division de tension et de courant. La formule de division de la tension donnera les tensions en série même si le courant n'est pas connu.
De la même façon, la formule de division de courant donnera le courant des branches ou courants dérivés, sans pour autant devoir connaître la tension.
En fin de compte, nous considérerons un diviseur de tension à branches en parallèle parcourues par des courants de charge. La conception d'un tel diviseur de tension chargé s'applique au cas important des prises de tensions connectées sur l'alimentation d'un appareillage électronique.
Ce chapitre traite des sujets suivants:
6.1 Diviseurs de tension
6.2 Diviseur de courant à deux résistances en parallèle
6.3 Division de courant par des conductances en parallèle
6.4 Diviseur de tension à courants de charge en parallèle
6.5 Conception d'un diviseur de tension chargé
6.1 DIVISEURS DE TENSION
Le même courant circule dans toutes les résistances d'un circuit série. Les chutes de tension sont données par le produit IR.
Ces tensions IR sont donc proportionnelles aux résistances en série. Plus la résistance en série d'un circuit est grande, plus sa tension IR est grande elle aussi.
Des résistances égales présentent la même chute V=IR.
Si R1 = 2 R2, alors V1 = I1R1 = 2 I1R2 = 2 V2, d'où V1 = 2 V2.
Tout jeu de résistances en série constitue un diviseur de tension. La chute de tension V=IR de chaque résistance est égale à sa partie proportionnelle de la tension appliquée, ce qui s'écrit, sous forme mathématique:
V = R / RT x VT
Exemple 1
Trois résistances R1, R2 et R3 de 50 kΩ sont disposées en série aux bornes d'une source de tension de 180 V.
Déterminer la chute de tension IR aux bornes de chacune.
Réponse 60 V.
En effet, ces trois résistances étant égales, chacune est le tiers de la résistance totale du circuit, chacune absorbe le tiers de la tension totale appliquée.
Mathématiquement, il viendra:
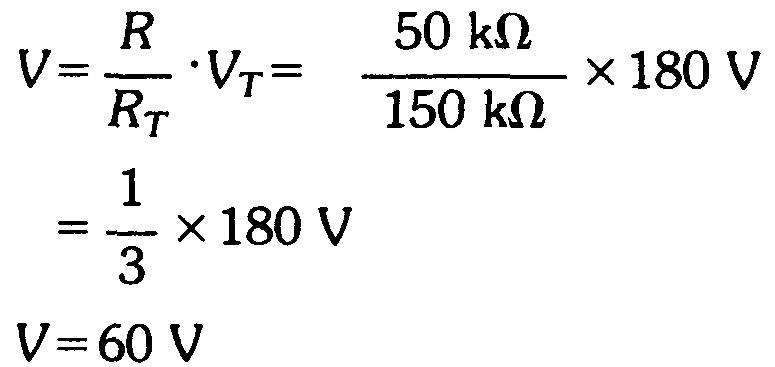
II importe que R et RT soient exprimés dans les mêmes unités.
Dans ce cas V est exprimé dans la même unité que VT.
Le circuit de la figure 6-1 constitue un autre exemple de diviseur de tension proportionnel.
Soit à calculer la tension entre les bornes de R3. Nous pouvons calculer cette tension soit par la formule IR3, soit par la formule (6.1) de la partie proportionnelle de VT.
Les deux résultats seront identiques.
Dans la méthode proportionnelle, V3 est les 20/100 de la tension appliquée car R3 est de 20 kΩ et RT de 100 MΩ.
V3 est donc égal à 20/100 x 200 V, soit 1/50 x 200 V, donc 40 V.
De la même façon,
V2 = 30/100 x 200 V = 3/10 x 200 V = 60 V
et V1 = 50/100 x 200 V = 1/2 x 200 V = 100 V.
Leur somme V1 + V2 + V3 = 40 V + 60 V + 100 V = 200 V est donc égale à VT.
Par la méthode du courant, on aura I = VT/RT = 200 V / 100 MΩ = 2 mA.
Alors V3 = I x R3 = 2 mA x 20 kΩ = 40 V.
De la même façon, V2 = 2 mA x 30 kΩ = 60 V et V1 = 2 mA x 50 kΩ = 100 V.
Ces valeurs sont égales à celles obtenues par la méthode proportionnelle selon la formule (6.1).
Figure 6-1 Un jeu de résistances en série constitue un diviseur de tension proportionnel: chaque VR = (R / RT) x VT.
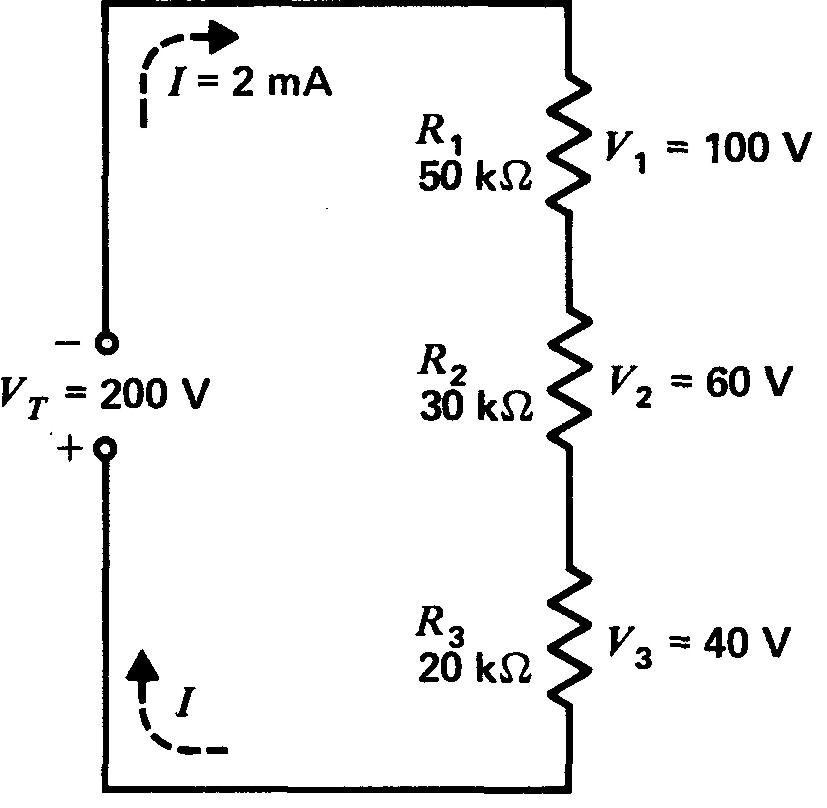
Dans le cas de deux tensions en série, il suffit d'en calculer une, sa soustraction de VT donnera l'autre.
La chute de tension en série étant proportionnelle à la résistance, il s'ensuit qu'une très petite résistance R présente une chute IR en série négligeable par rapport à celle engendrée par une résistance R beaucoup plus grande.
La figure 6-2 illustre un cas de ce genre: les résistances R1 de 1 kΩ et R2 de 999 kΩ sont en série et la tension VT est de 1000 V.
Figure 6-2 La résistance R1 est très petite par rapport à R2 en série avec elle. La tension V1 est donc elle aussi très petite par rapport à V2.
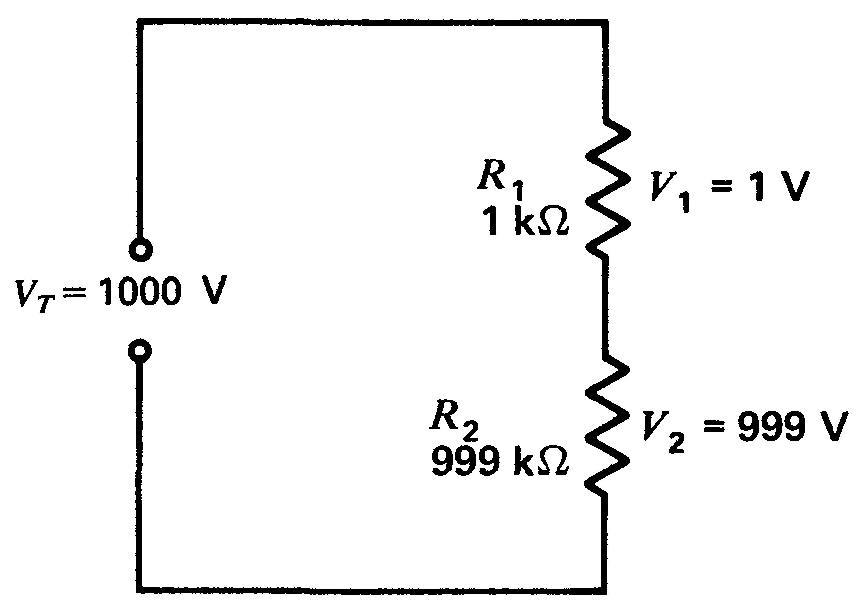
Selon la formule du diviseur de tension, on aura V1 = 1/1000 x 1000 V = 1 V et V2 = 999/1000 x 1000 V = 999 V, soit pratiquement toute la tension appliquée.
De plus, le courant de 1 mA circulant à travers R1 et R2 est presque entièrement déterminé par la résistance R2 de 999 kΩ.
Le courant I pour RT est de 1000 V / 1000 MΩ = 1 mA, celui pour R2 de 999 kΩ seul serait de 1,001 mA.
L'avantage de l'utilisation de la formule du diviseur est de trouver la chute de tension proportionnelle à partir de VT et des résistances en série sans connaître I.
Le calcul de I prendrait, pour des valeurs disgracieuses de R, plus de temps que le calcul des tensions. Il est possible dans de nombreux cas de déterminer approximativement la valeur de la division de tension sans effectuer aucun calcul.
Problèmes pratiques 6.1 (réponses à la fin du chapitre)
Considérer la figure 6-1:
(a) Calculer RT;
(b) Quelle fraction de la tension appliquée est V3?
6.2 DIVISEUR DE COURANT À DEUX RÉSISTANCES EN PARALLÈLE
II est souvent nécessaire de calculer le courant circulant dans chaque branche d'un réseau de résistances en parallèle à partir de la valeur de ces résistances et de celle de IT, sans connaître la tension entre les bornes du réseau parallèle.
La solution de ce problème repose sur la remarque suivante: le courant circulant dans une des deux branches d'un réseau parallèle est inversement proportionnel à la somme des résistances.
La figure 6-3 illustre un tel cas.
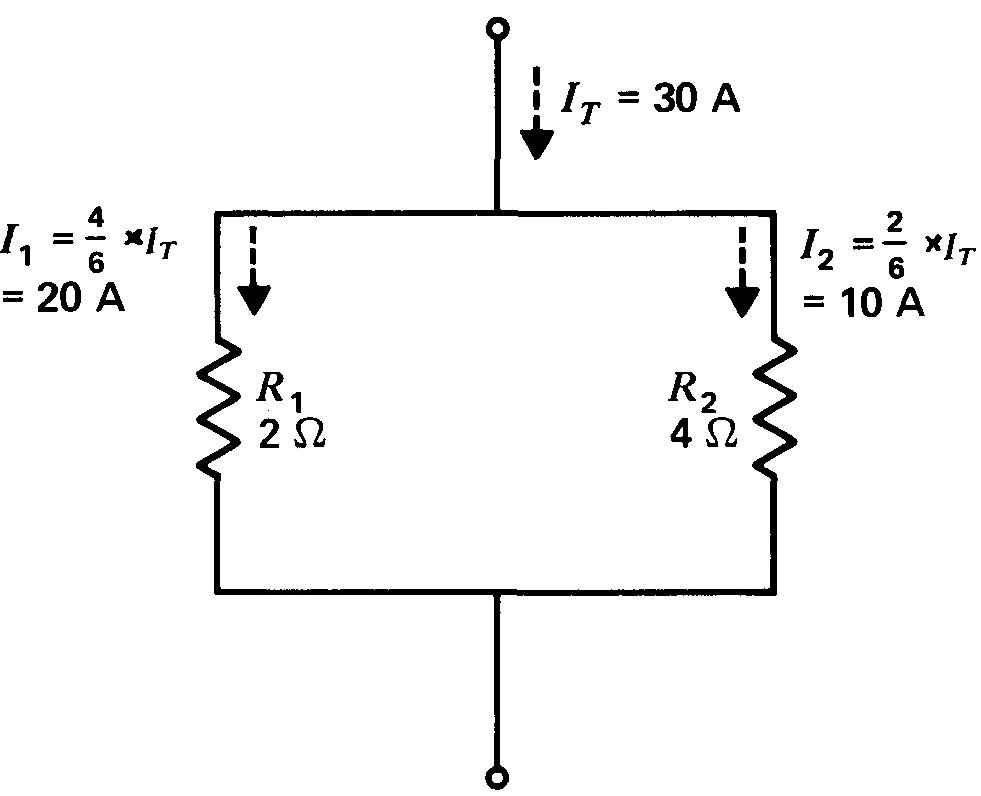
Figure 6-3 Division d'un courant par deux branches en parallèle. Chaque I est inversement proportionnel à R. La plus petite résistance R est parcourue par le plus grand courant I.
Les courants I1 et I2 des branches 1 et 2 s'obtiennent selon les expressions:
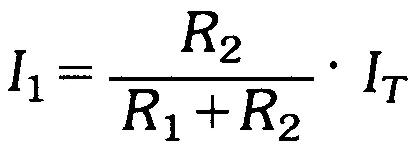 (6.2)
(6.2)
et
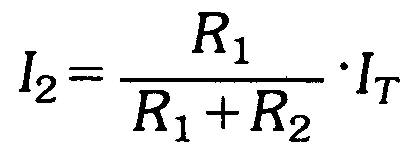
Remarquer que R2 apparaît au numérateur de I1 et que R1 apparaît à celui de I2. Cela provient du fait que le courant circulant dans une branche est inversement proportionnel à la résistance de cette branche. Le dénominateur, le même dans les deux expressions, est égal à la somme des résistances.
On aura, pour l'exemple illustré à la figure 6-3, dans lequel IT = 30 A, R1 = 2Ω et RΩ = 4Ω:
I1 = (4 / (2 + 4)) x 30 = 4/6 x 30 = 2/3 x 30 = 20 A
et, pour l'autre branche:
I2 = (2 / (2 + 4)) x 30 = 2/6 x 30 = 1/3 x 30 = 10 A
Les résistances étant toutes exprimées dans la même unité, l'unité des courants des branches est celle utilisée pour IT. On pourrait par exemple exprimer R en kilohms et I en milliampères.
Il n'est pas nécessaire en réalité de calculer les deux courants. Il suffit d'en calculer un, sa soustraction du courant total IT donnant l'autre.
Remarquer que la division d'un courant dans un réseau parallèle est le contraire de la division d'une tension dans un réseau série.
Dans le cas d'un réseau série, plus une résistance R, est grande, plus sa chute de tension IR, proportionnelle à la résistance R, sera grande; dans le cas d'un réseau parallèle, plus une résistance R est petite, plus le courant qui la traverse V/R, inversement proportionnel à la résistance R, sera grand.
Ainsi, à la figure 6-3, le courant I1 de 20 A est le double du courant I2 de 10 A, car la résistance R1 de 2Ω est la moitié de la résistance R2 de 4Ω. Le courant divisé I est donc inversement proportionnel à la résistance R qu'il traverse.
Cette caractéristique du réseau parallèle, le courant I divisé inversement proportionnel à la résistance R qu'il traverse, entraîne qu'une très grande résistance R a peu d'effet sur une résistance R beaucoup plus petite disposée en parallèle.
Considérons par exemple le circuit diviseur d'un courant IT de 1000 mA de la figure 6-4.
Figure 6-4 Très grande résistance R2 en parallèle avec R1 très petit courant I2 par rapport à I1.
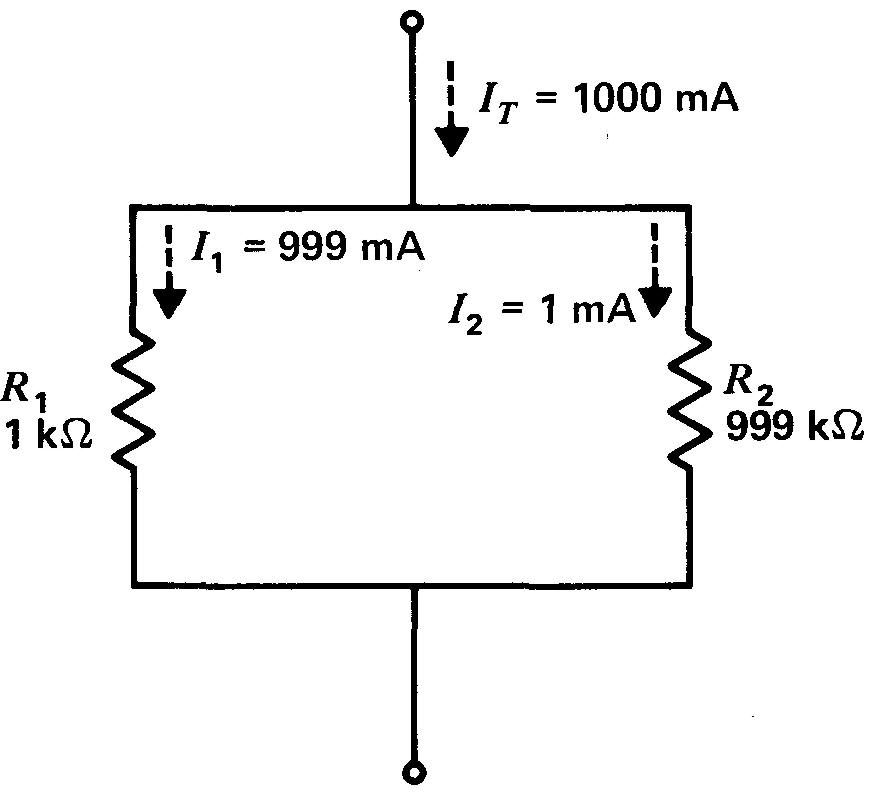
Il présente une résistance R2 de 999 kΩ en parallèle avec une résistance R1 de 1 kΩ.
Les courants des branches seront:
I1 = 999/1000 x 1000 ma = 999 mA
I2 = 1/1000 x 1 1000 ma = 1 mA
Les 999 mA de I1 constituent presque la totalité du courant d'alimentation de 1000 m A et cela parce que R1 est très petit par rapport à R2.
La formule (6.2) du diviseur de courant n'est valide que pour les réseaux à deux branches. Cela tient au fait que le courant divisé I de chaque branche est inversement proportionnel à la résistance R qu'il traverse.
Par contre, la formule (6.1) du diviseur de tension est valide quel que soit le nombre de résistances en série. Cela tient au fait que chaque chute de tension V=IR est directement proportionnelle à la résistance R qui la provoque.
Il est possible, pour un plus grand nombre de branches, de combiner ces dernières de manière à ne considérer que deux courants divisés à la fois.
La meilleure méthode, cependant, est de recourir aux conductances en parallèle, puisque I et G sont directement proportionnels, comme il est expliqué dans la section suivante.
Problèmes pratiques 6.2 (réponses à la fin du chapitre)
Considérer la figure 6-3:
(a) Calculer le rapport de R2 à R1,
(b) Calculer le rapport de I2 à I1.
6.3 DIVISION D'UN COURANT PAR DES CONDUCTANCES EN PARALLÈLE
Se rappeler que la conductance G = 1/R.
La conductance et le courant sont donc directement proportionnels. Une plus grande conductance permet le passage d'un plus grand courant, et ce pour la même valeur V.
Le courant de chaque dérivation est, peu importe le nombre de branches:
I = G/GT x IT (6.3)
Expression dans laquelle G est la conductance d'une branche et GT, la somme de toutes les conductances en parallèle.
L'unité de la conductance G est le siemens (S).
Remarquer que la formule (6.3) de division des courants proportionnellement à G est semblable à la formule (6.1) de division des tensions en série proportionnellement à R. Cela tient au fait que les deux formules représentent toutes deux une proportion directe.
En guise d'exemple d'utilisation de la formule (6.3), reportons-nous à la figure 6-3 et déterminons le courant des branches en considérant G au lieu de R.
On aura G1 = 1/R1 = 1/2 Ω = 0,5 S
et G2 = = 1/R2 = 1/4 Ω = 0,25 S
d'où GT = G1 + G2 = 0,5 S+ 0,25 S = 0,75 S.
Et puisque IT=30 A, on aura successivement:
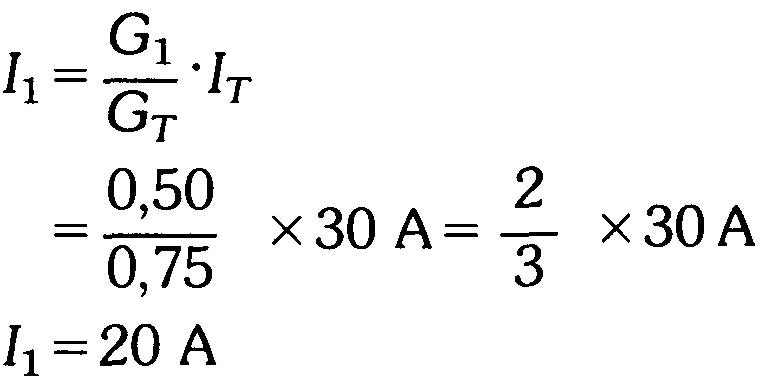
Ce courant I1 est de même valeur que celui calculé auparavant.
On en tire que I2 = 30 A - 20 A = 10 A.
La figure 6-5 représente un circuit parallèle à trois branches.
Figure 6-5 Diviseur de courant à trois conductances en parallèle G1, G2 et G3. Les conductances s'expriment en siemens, symbole S. Le courant I de chaque branche est directement proportionnel à la conductance G de cette branche.
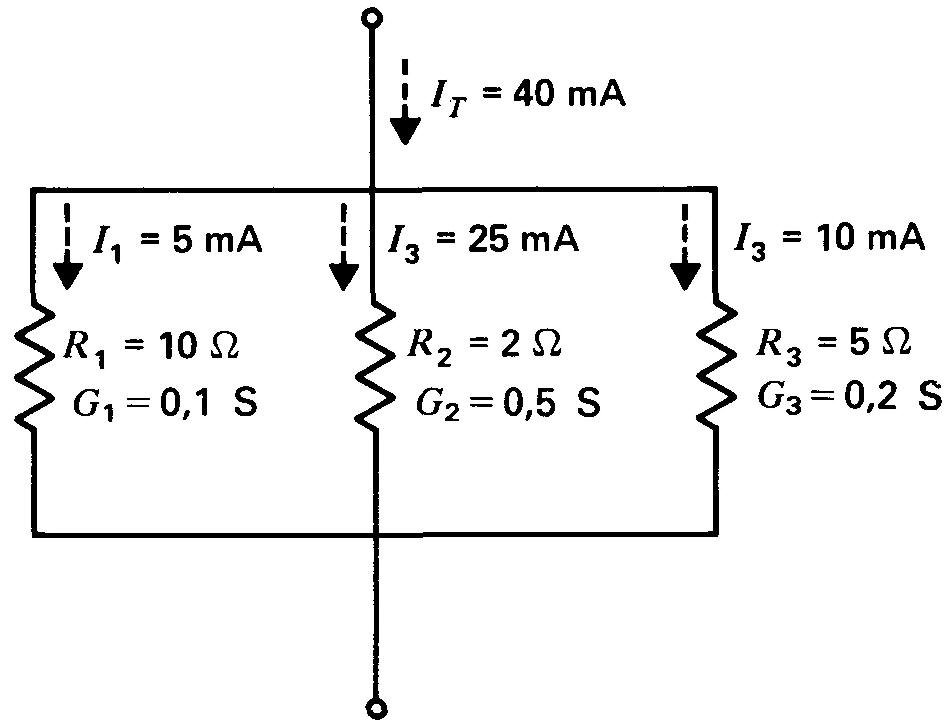
On aura G1 = 1/R1 = 1/10 Ω = 0,1 S, G2 = 1/R2 = 1/2 Ω = 0,5 S et G3 = 1/R3 = 1/8 Ω = 0,2 S.
Ce qui donne GT = 0,1 S + 0,5 S + 0,2 S = 0,8 S. Le courant IT donné est de 40 mA.
On aura:
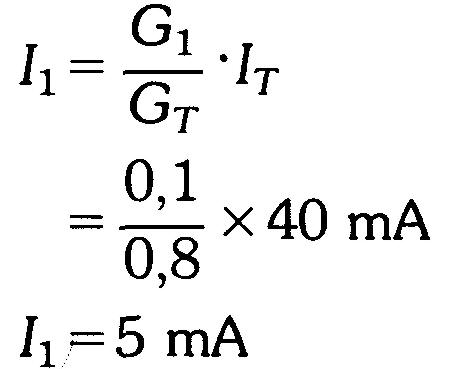
On obtient de la même façon I2 = 5/8 x 40 mA = 25 mA, I3 = 2/8 x 40 mA = 10 mA et la somme I1 + I2 +I3 = 5 mA + 25 mA + 10 mA = 40 mA, soit IT.
Le circuit envisagé ne comporte que trois branches, mais la formule est utilisable quel que soit le nombre de conductances en parallèle à cause de la proportion directe entre I et G.
Problèmes pratiques 6.3 (réponses à la fin du chapitre)
Considérer la figure 6-3:
(a) Calculer le rapport de G3 à G1,
(b) Calculer le rapport de I3 à I1.
6.4 DIVISEURS DE TENSION À COURANTS DE CHARGE EN PARALLÈLE
Les diviseurs de tension vus jusqu'à présent ne comprennent qu'un jeu de résistances en série sans aucun courant dérivé.
Et pourtant, en pratique, un diviseur de tension comporte souvent une prise de prélèvement d'une portion de VT destinée à alimenter une charge qui réclame une tension inférieure à VT.
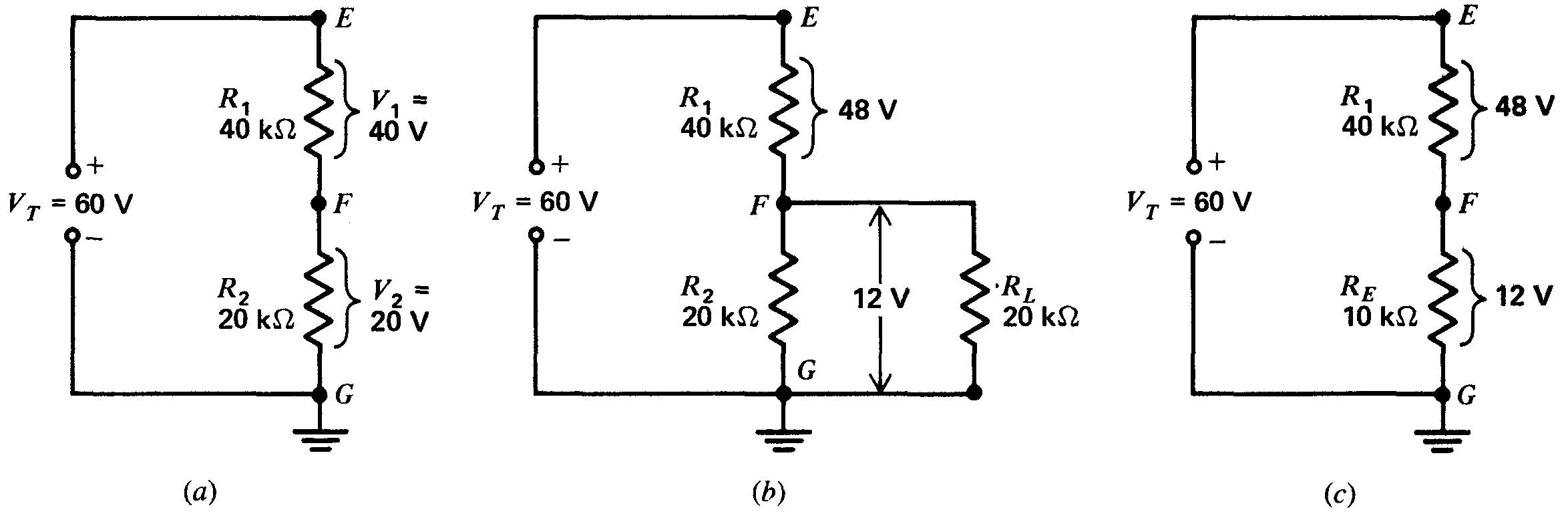
La charge ajoutée constitue alors une branche en parallèle disposée aux bornes d'une partie du diviseur. On constate, à la figure 6-6, que l'ajout d'une branche parallèle réduit la tension entre les bornes de dérivation.
Figure 6-6 Effet d'une charge en parallèle sur une portion d'un diviseur de tension:
(a) R1 et R2 en série sans dérivation de courant;
(b) tension réduite entre les bornes de R2 du fait du branchement de RL;
(c) circuit équivalent du diviseur de tension chargé.
Raison de la décroissance de la tension chargée
La figure 6-6a représente un diviseur de tension seul constitué des deux résistances R1 et R2, ces résistances formant un simple diviseur proportionnel série entre les bornes de la source VT de 60 V; R1 est de 40 kΩet R2, de 20 kΩ, soit une résistance RT de 60 kΩ.
D'où l'on tire I = 60 V / 60 kΩ = 1 mA.
La tension V1, entre les bornes de R1, est de 40/60 x 60 V = 40 V. De la même façon, V2 = 20/60 x 60 = 20 V.
Remarquer que V1 + V2 = 40 V + 20 V = 60 V, ce qui est bien la tension totale appliquée.
Le branchement en (b) de la résistance RL de 20 kΩ en dérivation change cependant la résistance équivalente entre la prise F et la masse G. Cette modification des proportions des résistances change la division de tension.
La résistance de F à G, constituée des résistances R2 et RL en parallèle égales chacune à 20 kH, est maintenant de 10 kO. Cette résistance équivalente de 10 kΩ, désignée par RE est représentée en (c).
Puisqu' aucune dérivation ne lui a été branchée, R1 est toujours de 40 kΩ.
La nouvelle résistance totale RT du diviseur tracé en (c) est de 40 kΩ + 10 kΩ = 50 kΩ.
De ce fait, VE, de F à G, est maintenant de 10/50 x 60 V = 12 V.
La tension aux bornes des résistances en parallèle R2 et RL est donc réduite à 12 V. C'est la valeur de la tension appliquée à RL à la prise F.
Remarquer que V1 entre les bornes de R1 passe à 48 V en (c).
En effet, V1 est maintenant de 40/s50 x 60 V = 48 V.
La somme V1 + V2 est de 12 V + 48 V = 60 V, ce qui redonne encore la tension totale appliquée.
Cheminement du courant pour RL
Tout le courant circulant dans ce circuit provient de la source VT.
Traçons le flux électronique pour RL. Il part du côté négatif de VT, traverse RL, se dirige vers la prise F et revient au diviseur du côté positif de VT via R. Ce courant IL circule à travers R1 mais non à travers R2.
Courant de fuite Les résistances R1 et R2 reçoivent, de plus, leur propre courant de la source. Ce courant qui traverse toutes les résistances d'un diviseur est le courant de fuite lB.
Le débit électronique pour IB part du côté négatif de VT via R2 et R1 pour revenir ensuite au côté positif de VT.
Le courant de fuite constitue un drain constant pour la source. Celui-ci, IB, présente cependant l'avantage de réduire les variations du courant total dans la source de tension pour différentes valeurs du courant de charge.
En résumé, donc, pour les trois résistances de la figure 6-6:
(a) RL n'est traversé que par son courant de charge IL;
(b) R2 n'est traversé que par le courant de fuite IB;
(c) R1 est parcouru à la fois par IL et par IB.
Problèmes pratiques 6.4 (réponses à la fin du chapitre)
Considérer la figure 6-6:
(a) Calculer le rapport R2/R1 de (a);
(b) Calculer le rapport RE/RT de (c).
6.5 CONCEPTION D'UN DIVISEUR DE TENSION CHARGÉ
La conception d'un diviseur de tension pratique, tel celui de la figure 6-7, repose sur les principes vus ci-dessus.
Figure 6-7 Diviseur de la tension de source VT en plusieurs tensions et obtention de courants de charge différents.
Pour le calcul de R1, R2 et R3, voir le texte.
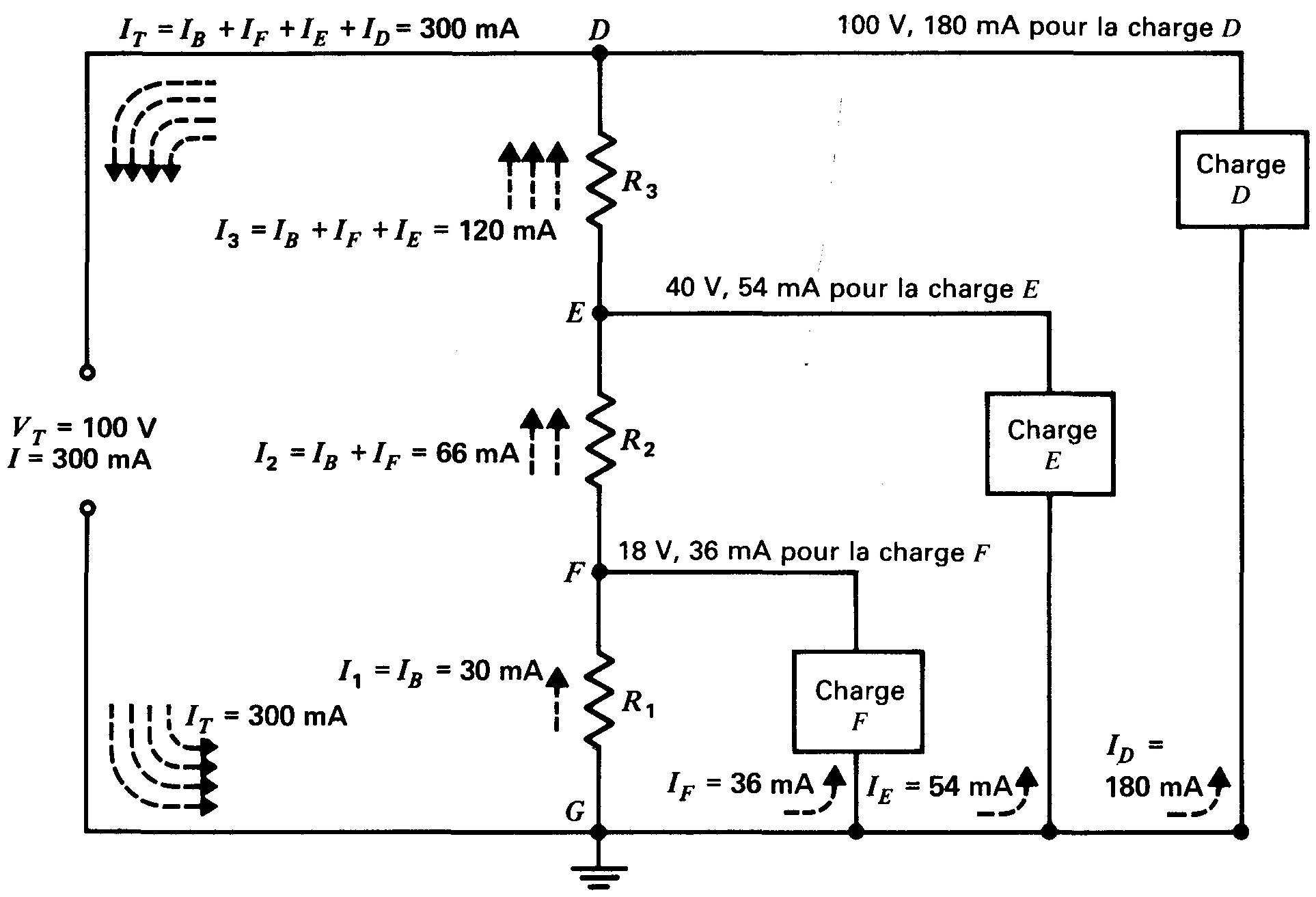
Ce type de circuit est utilisé à la sortie de l'alimentation d'un équipement électronique pour fournir à différentes prises des courants de charge différents sous des tensions différentes.
La charge D, par exemple, peut représenter le circuit collecteur-émetteur d'un ou plusieurs transistors de puissance nécessitant une alimentation collecteur de +100 V. La prise F peut, par exemple, représenter l'alimentation collecteur de 40 V pour des transistors de puissance moyenne.
Et, finalement, la prise F de 20 V peut, par exemple, fournir le courant de polarisation base-émetteur des transistors de puissance et la tension collecteur des petits transistors.
Remarquer les spécifications de charge de la figure 6-7.
La charge F réclame 18 V entre la prise F et la masse. Un courant de dérivation de 36 mA circulera à travers la charge F, une fois la tension de 18 V fournie.
De la même façon, le courant IE à travers la charge E sera de 54 mA si la tension à la prise E est de 40 V.
De plus, la tension VT de 100 V fait circuler un courant ID de 180 m A à travers la charge D.
Le courant total des charges est donc de 36 mA + 54 mA + 180 mA = 270 mA.
On accepte en outre un courant de fuite IB à travers le diviseur entier d'environ 10 % du courant total des charges.
Pour l'exemple traité ci-dessus on prendra, par exemple, IB = 30 mA.
Le courant total fourni par la source sera donc de 270 mA + 30 mA = 300 mA.
Rappelons que le courant IB de 30 mA circule à travers R1, R2 et R3.
Concevoir le diviseur illustré à la figure 6-7 revient donc à déterminer les résistances R1, R2 et R3, compte tenu des tensions spécifiées. Chaque résistance R sera déterminée par le rapport V/I. Cela nous impose de trouver la valeur pertinente de V et celle de I pour chaque portion du diviseur.
Calcul du courant circulant à travers chaque R
Calcul du courant circulant à travers chaque R Commençons par la résistance Rx car son courant est le courant de fuite de 30 mA lui-même.
Aucun courant de charge ne circule dans R1, de sorte que le courant I1 à travers R1 est de 30 mA.
Le courant IF de 36 mA circulant dans la charge F revient à la source via R2 et R3.
Considérons R2 seul: son courant I2 est égal au courant IF de la charge F plus le courant de fuite IB de 30 mA, soit
I2 = 36 mA + 30mA = 66mA.
Le courant IE de 54 mA circulant dans la charge E revient à la source via R3 seul. Cette résistance J?3 est aussi parcourue par le courant IF de 36 mA et par le courant IB de 30 mA.
Le courant I3 à travers R3 est donc de 54 mA + 36 mA + 30 mA=120 mA. Ces valeurs I1, I2 et I3 apparaissent au tableau 6-1.
Tableau 6-1 Valeurs calculées du diviseur de tension de la figure 6-7

Remarquer que le courant de charge ID de la charge D à la partie supérieure de la figure 6-7 ne circule pas à travers R3 ni à travers aucune des résistances du diviseur.
Ce courant ID de 180 mA est cependant le principal courant de charge circulant à travers la source de tension appliquée. Le courant de fuite et des charges de 120 m A, ajouté au courant de charge ID de 180 mA donne un courant total IT, circulant dans la ligne principale de l'alimentation, de 300 mA.
Calcul de la tension entre les bornes de chaque résistance R La tension aux prises de la figure 6-7 est le potentiel par rapport à la masse.
La tension dont nous avons besoin est celle entre les bornes de chaque R.
1La tension Vx entre les bornes de R1 est la valeur 18 V indiquée par rapport à la masse, car une extrémité de R1 lui est reliée.
Par contre, la tension entre les bornes de R2 est la différence entre le potentiel de 40 V au point E et celui de 18 V au point F.
D'où V2 = 40 V - 18V = 22 V.
De la même façon, V3 est la différence entre le potentiel de 100 V au point D moins celui de 40 V au point E,
soit 1/3 = 100 V-40 V = 60 V.
Ces valeurs V1, V2 et V3 apparaissent au tableau 6-1.
Calcul de chaque R Nous pouvons maintenant calculer les résistances R1, R2 et R3 par le rapport V/I pertinent.
Selon les valeurs énumérées au tableau 6-1, on aura successivement:

Le montage de ces résistances R1, R2 et R3 selon le diviseur de tension de source 100 V illustré à la figure 6-7 assurera à chaque charge la tension spécifiée et son courant nominal.
Problèmes pratiques 6.5 (réponses à la fin du chapitre)
Considérer la figure 6-7:
(a) Que vaut le courant de fuite IB parcourant R1, R2 et R3?
(b) Que vaut la tension de la charge E, de la prise E à la masse?
(c) Que vaut la tension V2 aux bornes de R2?
Résumé
1. Dans un circuit série, la tension VT est divisée en chutes de tension IR proportionnelles aux résistances.
Chaque chute VR = (R/RT) x VT, quel que soit le nombre de résistances série. Plus la résistance série R est grande, plus sa chute de tension est grande elle aussi.
2. Dans un circuit parallèle, le courant IT est divisé en courants de branche. Chaque courant I est inversement proportionnel à la résistance R de la dérivation. La division inversement proportionnelle des courants dérivés donnée par la formule (6.2) n'est valable que pour deux résistances seulement. Plus la résistance R de la dérivation est petite, plus le courant dérivé est grand.
3. Le courant IT est divisé en courants dérivés directement proportionnels à chaque conductance G, quel que soit le nombre de dérivations en parallèle. Chaque courant I = (G/GT) x IT.
4. Un diviseur de tension série comporte souvent une prise d'alimentation d'une charge en parallèle, comme l'illustre la figure 6-6. L'existence d'un courant de charge réduit la tension de la prise.
5. La conception d'un diviseur de tension chargé, tel celui illustré à la figure 6-7, implique le calcul de chaque R. Déterminer tout d'abord le courant I et la différence de potentiel V relatifs à chaque R. Puis effectuer R = V/I
Exercices de contrôle
(Réponses aux exercices de contrôle)
Voici un moyen de contrôler si vous avez bien assimilé le contenu de ce chapitre. Ces exercices sont uniquement destinés à vous évaluer vous-même.
Répondre par vrai ou faux.
1. Dans un diviseur de tension série, chaque tension IR est proportionnelle à sa résistance R.
2. Dans le cas de branches en parallèle, chaque courant I de branche est inversement proportionnel à la résistance R de la branche considérée.
3. Dans le cas de branches en parallèle, chaque courant I de branche est directement proportionnel à la conductance G de la branche considérée.
4. La formule (6.2) des diviseurs de courant parallèle peut être utilisée pour trois résistances ou plus.
5. La formule (6.3) des diviseurs de courant parallèle est valide pour cinq branches de conductance en parallèle ou plus.
6. Dans le diviseur de tension série de la figure 6-1, la tension V1 est égale à 2,5 fois V3 du fait que R1 est égal à 2,5 fois R3.
7. Dans le diviseur de courant parallèle de la figure 6-3, I1 est le double de I2 du fait que R1 est la moitié de R2.
8. Dans le diviseur de courant parallèle de la figure 6-5, I3 = 5 I1 du fait que G3 = 5 G1.
9. Dans le circuit de la figure 6-6b, IL parcourt RL, R2 et R1.
10. Soit le circuit de la figure 6-7, le courant de fuite IB parcourt R1, R2 et R3.
Questions
1. Définir un diviseur de tension.
2. Définir un diviseur de courant.
3. Donner deux différences entre un diviseur de tension et un diviseur de courant.
4. Donner trois différences entre la formule (6.2) des résistances en dérivation et la formule (6.3) des conductances en dérivation.
5. Définir le courant de fuite.
6. Quelle est la principale différence entre les circuits (a) et (b) de la figure 6-6?
7. Considérer la figure 6-1 et expliquer pourquoi la tension V1 est en série conjonction avec V2 et V3, mais en série opposition avec VT. Indiquer la polarité de chaque chute IR.
8. Démontrer la formule (6.2) des courants dérivés d'un montage parallèle à deux résistances. (Suggestion: la tension entre les bornes du montage parallèle est IT x RT et la résistance RT = (R1 x R2) / (R1 + R2).
Problèmes
(Réponses aux problèmes de numéro impair)
1. Une résistance R1 de 200 Ω est en série avec une résistance R2 de 400 Ω et une résistance R3 de 2 kΩ. La tension appliquée est de 52 V. Calculer V1, V2 et V3.
2. La source de tension de 200 V d'un diviseur de tension fournit 10 mA à deux résistances série R1 et R2. La tension V2 aux bornes de R2 est de 50 V. Ce diviseur ne comporte aucune charge de dérivation. Calculer R1 et R2.
3. Déterminer le courant de fuite circulant à travers les résistances R1 et R2 du circuit de la figure 6-6b.
4. Soit un diviseur de courant à deux branches. IT = 7 mA, R1 = 20 kΩ et R2 = 56 kΩ. Calculer I1 et I2.
5. Soit un diviseur de courant à trois branches 1, 2 et 3 en parallèle. On a G1 = 1000 µS, G2 = 2000 µS et G3 = 10 000 µS.
IT = 39 mA. Calculer I1, I2 et I3.
6. Considérer la figure 6-3. Calculer la résistance RT des deux branches et la tension aux bornes du montage parallèle par la formule VT = IT x RT.
7. Soit le diviseur de tension illustré à la figure 6-7. Déterminer la résistance équivalente des charges D, E et F.
8. Soit le diviseur de tension illustré à la figure 6-7. Calculer la puissance dissipée dans R1, R2 et R3.
9. Concevoir un diviseur de tension similaire à celui de la figure 6-7, comprenant trois résistances R1, R2 et R3 aux bornes d'une source de tension de 48 V et comportant les charges suivantes:
48 V à 800 mA, 28 V à 300 mA et 9 V à 100 mA. Prendre un courant de fuite IB de 120 m A.
Réponses aux problèmes pratiques
