Chapitre 4 - les circuits parallèle

Mon premier cours en électronique

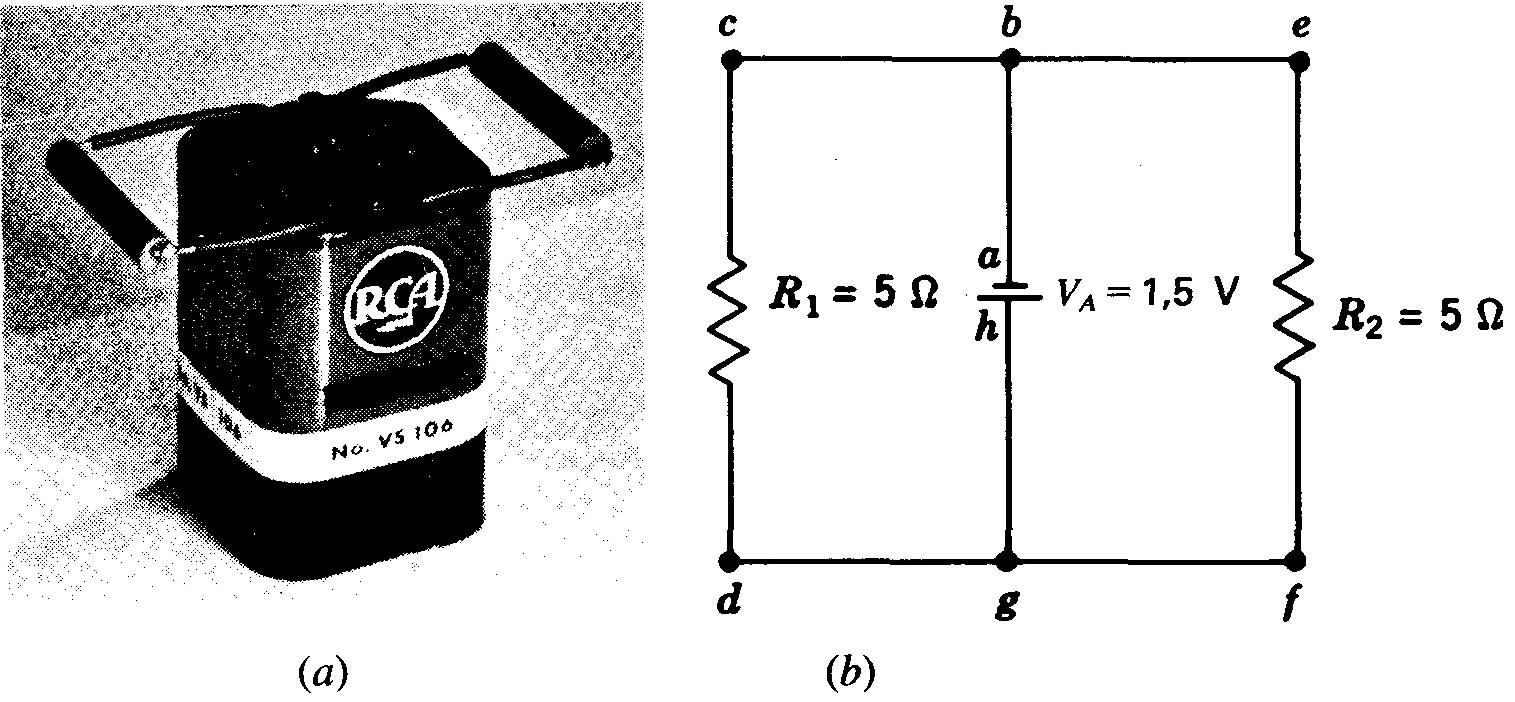
Lorsque l'on branche deux composants ou plus aux bornes d'une source de tension, comme on l'indique sur la figure 4-1, ils constituent un circuit parallèle.

Figure 4-1 Circuit parallèle: (a) photographie du câblage; (b) schéma.

Les résistances R1 et R2 sont montées en parallèle entre elles et en parallèle avec la pile. Chaque circuit parallèle constitue alors une branche dans laquelle circule un courant qui lui est propre.

Ainsi, dans le cas de circuits parallèle, une tension commune est appliquée aux bornes de toutes les branches, mais les courants dans les différentes branches peuvent être différents.

Ces caractéristiques sont inverses de celles des circuits série qui sont traversés par un même courant, les tensions aux bornes des différents composants pouvant être différentes.

Les caractéristiques essentielles des circuits parallèle sont exposées dans les sections suivantes:

4.1 La tension V_A appliquée est la même aux bornes de toutes les branches parallèle

4.2 Le courant circulant dans chaque branche est égal à V_A / R

4.3 Le courant principal I_T est égal à la somme des courants dans les différentes branches

4.4 Résistances en parallèle

4.5 Conductances en parallèle

4.6 Puissance totale dans les circuits parallèle

4.7 Analyse des circuits parallèle

4.8 Effets d'une coupure sur un circuit parallèle

4.9 Effets d'un court-circuit aux bornes des branches parallèle

4.1 LA TENSION V_A APPLIQUÉE EST LA MÊME AUX BORNES DE TOUTES LES BRANCHES PARALLÈLE

Les points a, b, c et e de la figure 4-1b correspondent effectivement à une liaison directe à la borne négative de la pile car les fils de branchement n'ont pratiquement aucune résistance.

 De la même manière, les points h, g, d, et f correspondent à une liaison directe à la borne positive de la pile.

Les deux résistances R1 et R2 sont directement branchées aux bornes de la pile; la différence de potentiel aux bornes de chacune est donc la même que la tension de la pile.

On en déduit que la tension aux bornes de composants montés en parallèle est la même.

Les branchements parallèle sont donc utilisés pour des circuits dont les composants doivent être branchés sur la même tension.

Les branchements des installations domestiques au réseau constituent une application courante des circuits parallèle; de nombreux appareils et lampes sont alors branchés en parallèle sur le secteur à 120 V (figure 4-2).

Figure 4-2 Ampoule d'éclairage et grille-pain branchés en parallèle sur le secteur à 120 V: (a) schéma de câblage; (b) schéma.

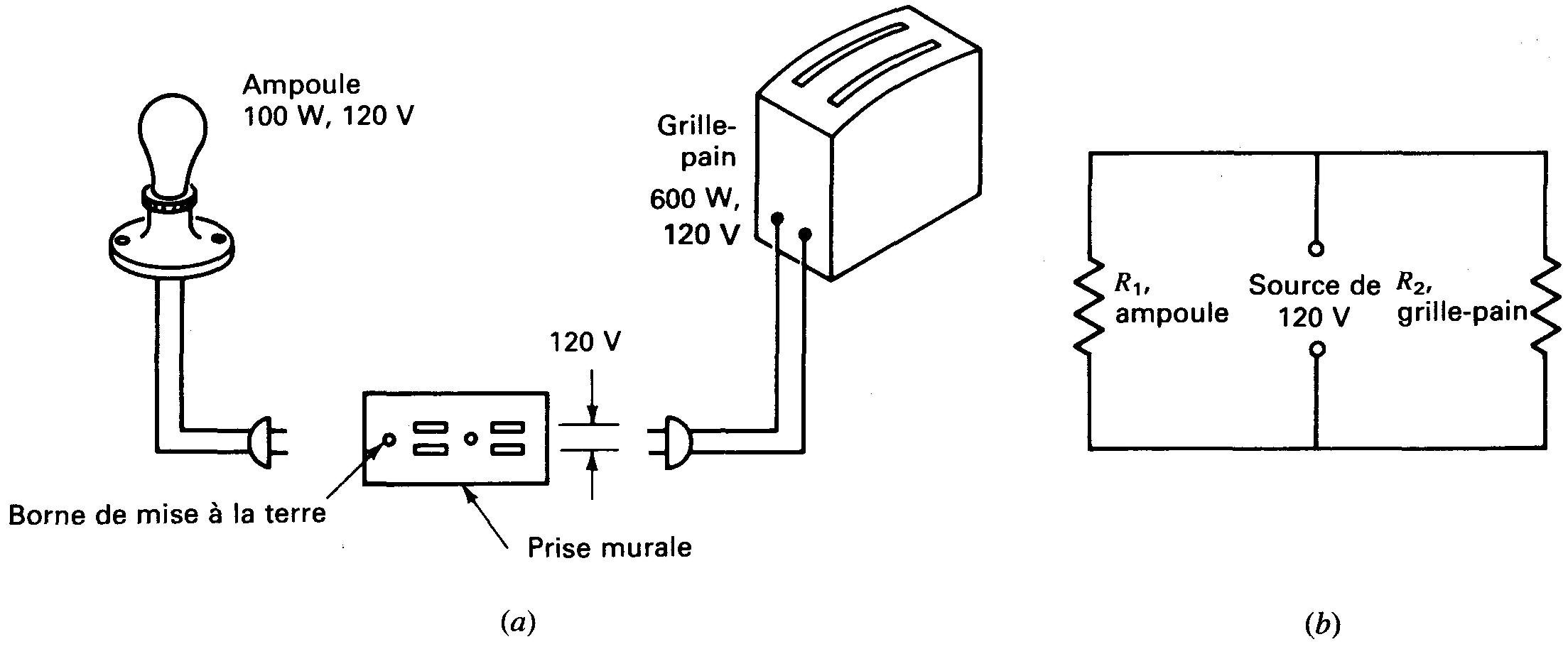
Entre deux bornes d'une prise murale, la différence de potentiel est de 120 V. Donc, toute résistance branchée à une prise de courant est soumise à une tension de 120 V.

L'ampoule d'éclairage est branchée sur une sortie, le grille-pain sur une autre; aux bornes de ces deux appareils, la tension est la même, soit 120 V.

Ainsi, lorsque tous les circuits de branchement sont raccordés en parallèle sur le réseau à 120 V, chaque appareil fonctionne de manière indépendante.

Problèmes pratiques 4.1 (réponses à la fin du chapitre)

(a) Soit la figure 4-1. Que vaut la tension commune aux bornes de R1 et R2?

(b) Soit la figure 4-2. Que vaut la tension commune aux bornes de la lampe et du grille-pain?

4.2 LE COURANT CIRCULANT DANS CHAQUE BRANCHE EST ÉGAL À V_A / R

Lorsqu'on applique la loi d'Ohm, il est important de noter que la valeur du courant est égale à la tension appliquée aux bornes du circuit, divisée par la résistance comprise entre les deux points du circuit auxquels cette tension est appliquée.

Sur la figure 4-3, une tension de 10 V est appliquée aux bornes d'une résistance R2 de 5 Ω, faisant circuler un courant de 2 A dans la résistance R2, entre les points e et f.

Figure 4-3 Le courant circulant dans chaque branche parallèle est égal à la tension V_A divisée par la résistance R de chaque branche.

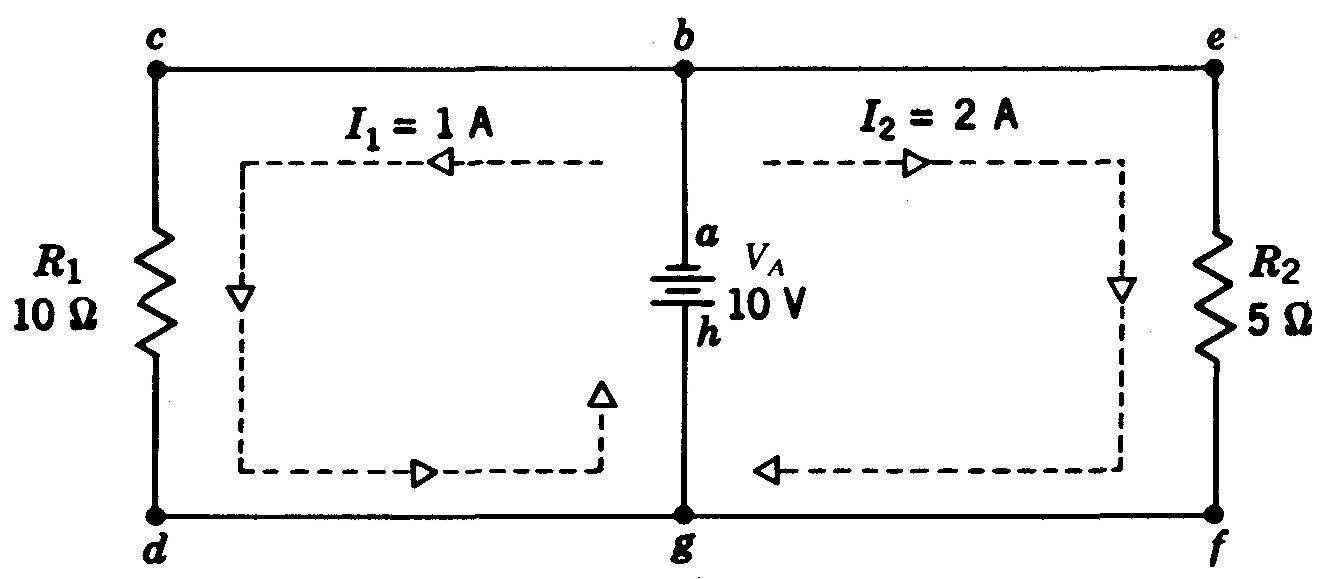
La tension de la pile est également appliquée aux bornes de la résistance R1montée en parallèle, ce qui correspond à une tension de 10 V aux bornes de 10 Ω.

Un courant de 1 A traverse ainsi la résistance R1 entre les points c et d. Pour une même valeur de la tension appliquée, le courant circulant dans R1 est plus faible car la résistance est différente.

Les valeurs précédentes sont calculées de la manière suivante:

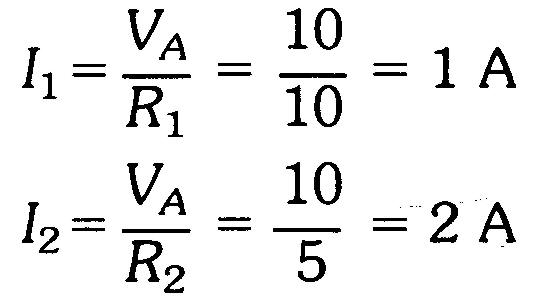
Comme dans tout circuit à une résistance, toute branche présentant moins de résistance permet la circulation d'un plus grand courant.

Si la résistance R1 avait la même valeur que la résistance R2, les deux courants de branches seraient égaux.

Par exemple, sur la figure 4.1b, chaque courant de branche a une valeur de 1,5 V / 5 Ω, soit 0,3 A.

Le courant circulant dans des circuits parallèle peut être différent lorsque ces circuits ont des résistances différentes, puisque la tension aux bornes des différentes branches est la même.

La source de tension génère une différence de potentiel entre ses deux bornes. Cette tension ne se déplace pas. Seul le courant circule le long du circuit.

Cette tension reste fixe et disponible aux bornes de la source; elle permet d'assurer la circulation des électrons suivant un circuit fermé, relié aux bornes de la source.

La valeur de I dans les différentes branches dépend de la valeur de la résistance de chacune d'elles.

Problèmes pratiques 4.2 (réponses à la fin du chapitre) Considérer la figure 4-3:

(a) Calculer la tension aux bornes de R1,

(b) Calculer le courant I1 parcourant R1,

(c) Calculer la tension aux bornes de R2;

(d) Calculer le courant I2 parcourant R2.

4.3 LE COURANT PRINCIPAL I_T EST ÉGAL À LA SOMME DES COURANTS DANS LES DIFFÉRENTES BRANCHES

Les composants devant être branchés en parallèle sont généralement câblés directement les uns aux autres, l'ensemble du montage parallèle étant ensuite branché aux bornes de la source de tension, comme le montre la figure 4-4.

Figure 4-4 Le courant de la ligne principale est égal à la somme des courants de branches. La connexion de g à a correspond au côté négatif de la ligne principale; la connexion de b à f correspond au côté positif,

(a) Schéma de câblage. Les flèches à l'intérieur des connexions correspondent au courant circulant dans R1 les flèches situées à l'extérieur correspondent au courant circulant dans R2.

(b) Schéma; I_T est le courant de ligne total.

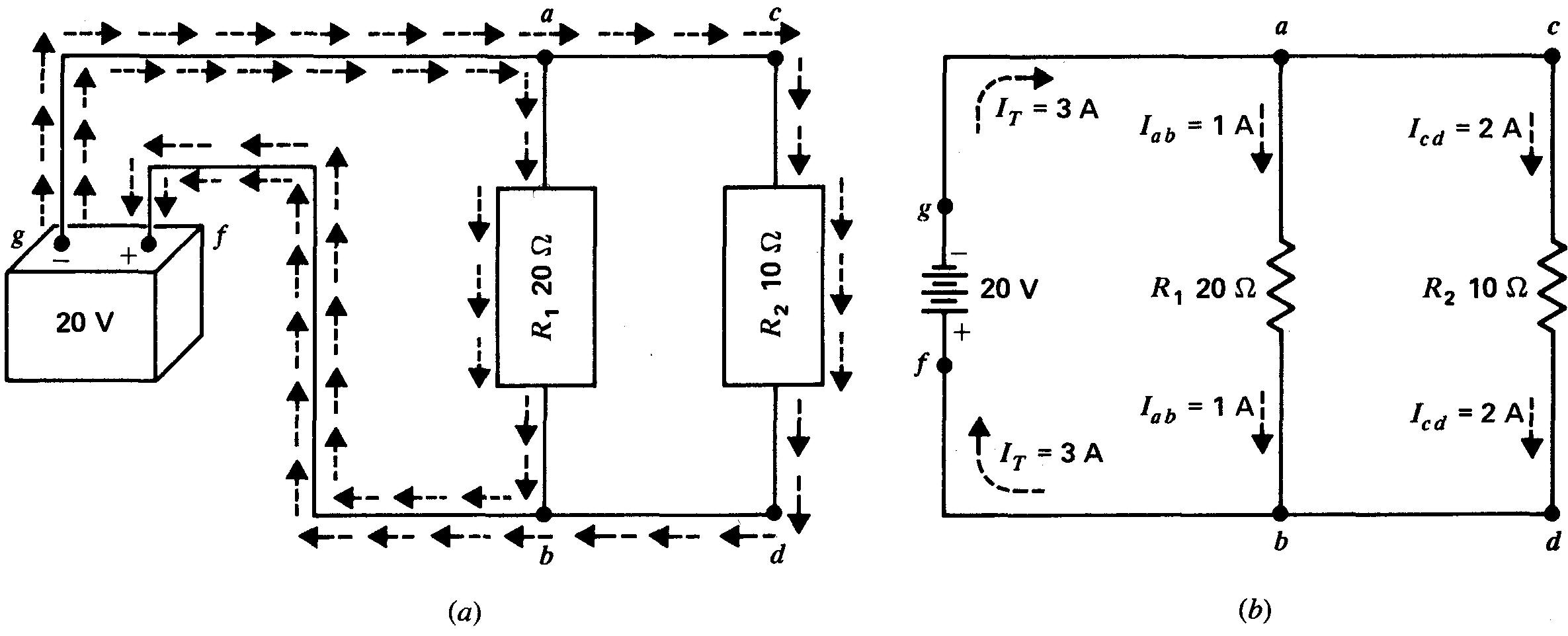
Le circuit obtenu est équivalent à celui réalisé en câblant chaque branche en parallèle directement aux bornes de la source de tension, comme le montre la figure 4-1, lorsque les fils de connexion ont une résistance pratiquement nulle.

Il est avantageux de ne prévoir qu'une seule paire de fils conducteurs pour relier toutes les branches à la source de tension; on
effectue en effet une économie de câblage.

La paire de fils reliant toutes les branches aux bornes de la source de tension est la ligne principale. Sur la figure 4-4, les fils allant de g vers a sur le côté négatif, et de b à f sur le circuit de retour, constituent la ligne principale.

À la figure 4-4b, une résistance R1 de 20 Ω étant branchée aux bornes d'une pile de 20 V, le courant traversant R1 sera de

20 V/ 20 Ω = 1 A

Ce courant correspond à un flux d'électrons partant de la borne négative de la source, traversant R1 puis retournant à la borne positive de la pile.

De même, la branche comportant une résistance R2 de 10 Ω branchée aux bornes de la pile possède son propre courant de

20 V / 10 Ω = 2

A circulant de la borne négative de la source, traversant R2 et retournant vers la borne positive, car il s'agit d'un circuit séparé pour la circulation des électrons.

Cependant, tous les courants du circuit partent d'une borne de la source de tension et retournent à la borne opposée en suivant un circuit fermé. Le courant dans la ligne principale est ainsi égal à la somme des courants de branches.

À la figure 4-4b, par exemple, le courant total de la ligne, partant du point g pour aller au point a, est de 3 A.

Le courant total au point de branchement (noeud) a se divise en ses courants de branches (un courant pour chacune des résistances de branches).

Le courant dans le circuit allant de a vers b et traversant R1 a une valeur de 1 A.

Le courant de l'autre branche, circuit a, c, d, b, traversant R2, est égal à 2 A.

Au noeud b, les électrons provenant des deux branches en parallèle se combinent de sorte que le courant circulant dans la ligne principale de retour de b à f a la même intensité de 3 A que dans l'autre portion de la ligne principale.

Le courant I_T circulant dans la ligne principale est donné par la formule:

I_T = I1 + I2 + I3 + ... + In    (4.1)

Cette règle s'applique, quel que soit le nombre de branches parallèle, que les résistances soient égales ou non.

Exemple 1

Trois résistances R1, R2 et R3 dont les valeurs respectives sont 20 Ω, 40 Ω et 60 Ω sont branchées aux bornes du secteur à 120 V.

Calculez l'intensité totale I_T du courant de ligne.

Réponse

Le courant I_T de la branche R1 est égal à 120 / 20, soit 6 A.

De même, R2 vaut 120 / 40, soit 3 A, et R3 vaut 120 / 60, soit 2 A.

Le courant total dans la ligne principale est:

I_T = I1 + I2 + I3 = 6 + 3 + 2 = 11 A

Exemple 2

Deux branches R1 et R2 aux bornes du secteur à 120 V tirent un courant total I_T de 15 A. Le courant de la branche R1 est de 10 A.

Quelle est la valeur du courant R2 dans la branche R2?

Réponse

R2 = I_T — I1 = 15 - 10

I2 = 5A

Remarquons que le courant de ligne I_T doit être supérieur à l'un quelconque des courants de branches; de même, tout courant de branche doit être inférieur à I_T.

Exemple 3

Les valeurs des courants de trois branches en parallèle sont de 0,1 A, 500 mA et 800 µA.

Calculez I_T.

Réponse

Pour pouvoir faire la somme des valeurs, il est nécessaire d'utiliser les mêmes unités.

Si l'unité de base est le mA, on aura 0,1 A = 100 mA, et 800 µA = 0,8 mA.

Par conséquent:

I_T= 100 + 500 + 0,8

I_T = 600,8 mA

Les courants en A, mA ou µA peuvent être additionnés car ils sont tous exprimés avec la même unité.

Problèmes pratiques 4.3 (réponses à la fin du chapitre)

(a) Les courants de branches parallèle sont

I1 = 1 A, I2 = 2 A et I3 = 3 A.

Calculer I_T.

(b) Le courant I_T de trois branches est de 6 A.

I1 = 1A, I2 = 2A.

Calculer I3.

4.4 RÉSISTANCES EN PARALLÈLE

La loi d'Ohm donne la résistance totale aux bornes de la ligne principale, dans un circuit parallèle:

diviser la tension commune aux bornes des résistances en parallèle par le courant total de toutes les branches.

Remarquez, en vous référant à la figure 4-5a, que la résistance de R1 et R2 en parallèle est remplacée par la résistance équivalente R_T qui est l'opposition au courant total de la ligne principale.

Figure 4-5 Résistances en parallèle:

(a) la résistance équivalente à l'ensemble des deux résistances R1 et R2 est la résistance R_T dans le circuit principal;

(b) circuit équivalent montrant la résistance équivalente R_T parcourue par le même courant R_T que l'ensemble des résistances en parallèle R1 etR2

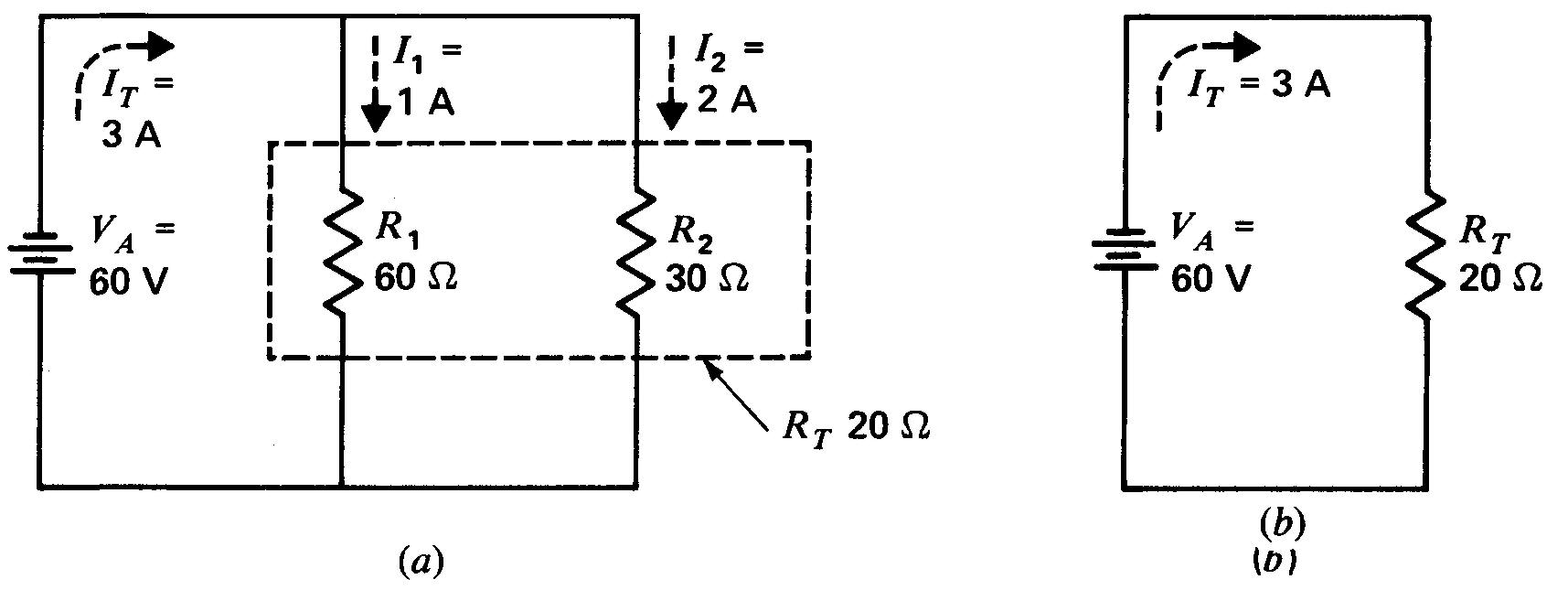
Par conséquent, la résistance totale R_T est égale à la tension appliquée sur la ligne principale divisée par le courant de la ligne, ce qui, dans cet exemple, donne 60 V / 3 A, soit 20 Ω

La charge totale connectée à la tension de source correspond à une résistance équivalente de 20 Ω qui aurait été connectée sur la ligne principale, comme le montre le circuit équivalent de la figure 4-5b.

Par conséquent, quel que soit le nombre des résistances en parallèle d'une valeur quelconque:

R_T = V_T / I_T

où I_T est la somme de tous les courants de branche et R_T, la résistance équivalente de toutes les branches en parallèle sur la source de tension V_A.

Exemple 4

Deux branches, chacune avec un courant de 5 A, sont connectées sur une source de 90 V.

Quelle est la valeur de la résistance totale équivalente R_T?

Réponse

Le courant total de la ligne I_T est 5 + 5 = 10 A.

Donc:

R_T = V_A / I_T = 90 / 10 = 9Ω

Jeu de résistances en parallèle

On appelle couramment un ensemble de branches parallèle un jeu de résistances en parallèle.

Dans la figure 4-5, le jeu de résistances en parallèle se compose de R1 de 60 Ω et de R2 de 30 Ω en parallèle. Leur résistance parallèle équivalente R_T est la résistance du jeu qui, dans cet exemple, est égale à 20 Ω.

Lorsqu'un circuit a un courant plus important, pour une même tension appliquée, l'augmentation de I correspond à une diminution de R en raison de leur relation inverse.

Par conséquent, la combinaison des résistances en parallèle R_T est toujours inférieure à la plus petite résistance de branche individuelle, car I_T doit être supérieur à tout courant de branche individuel.

Pourquoi R_T est inférieur à toute résistance R de branche

Au premier abord, on peut trouver étrange qu'un nombre plus élevé de résistances dans un circuit abaisse la résistance équivalente. Cette caractéristique des circuits parallèle est illustrée par la figure 4-6.

Figure 4-6 L'addition de plusieurs branches en parallèle augmente le courant I_T mais diminue la résistance R_T:

(a) une branche; (b) deux branches; (c) trois branches; (d) circuit équivalent à (c).

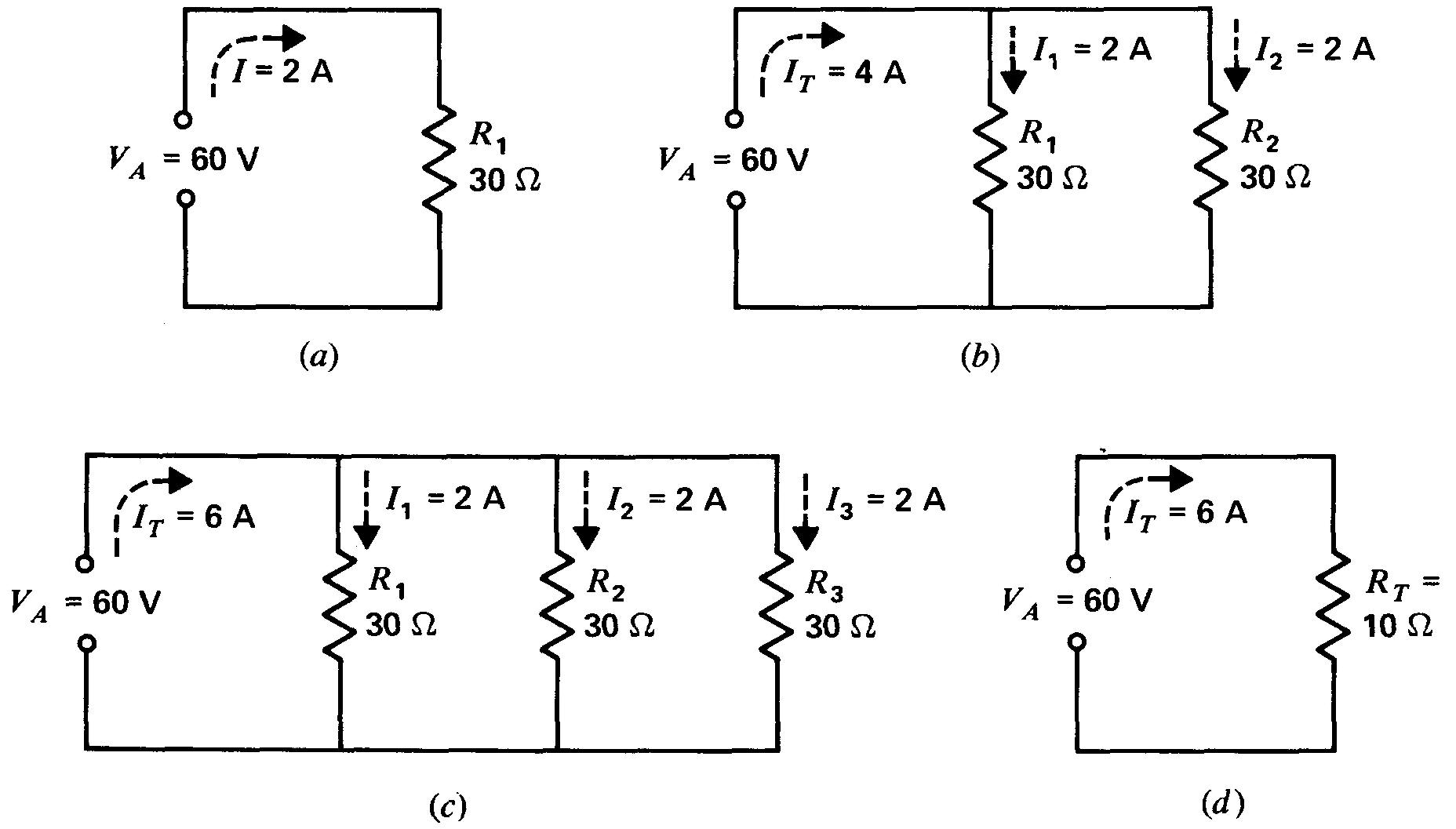
Remarquez que des résistances égales de 30 Ω chacune sont ajoutées aux bornes de la source, l'une après l'autre.

Le circuit en (a) n'a que R1, ce qui donne un courant de 2 A pour 60 V appliqués.

En (b), la branche R2 est ajoutée aux bornes de la même source V_A.

Cette branche est également parcourue par un courant de 2 A.

Or, le circuit parallèle a un courant de ligne total de 4 A en raison de I1 +I2.

Puis, on ajoute la troisième branche en (c) qui donne également un courant de 2 A pour I3.

Par conséquent, le circuit combiné à trois branches exige un courant de charge total de 6 A, qui est fourni par la source de tension.

La résistance combinée aux bornes de la source est alors de V_A / I_T qui vaut 60/6 ou 10 Ω.

Cette résistance équivalente R_T, représentant la charge entière sur la source de tension, apparaît en (d).

Un plus grand nombre de branches de résistances diminue la résistance combinée du circuit parallèle, car il faut plus de courant provenant de la même source de tension.

Formule de l'inverse de la résistance

Cette formule s'appuie sur la propriété que I_T est la somme de tous les courants des branches, d'où:

I_T = I1 + I2 + I3 + ... + In

Or, I_T = V / R_T.

De plus, chaque I = V / R.

Remplaçons, dans le membre de gauche I_T par V / R_T et chaque I dans le membre de droite par l'expression V/R correspondante.

Il deviendra:

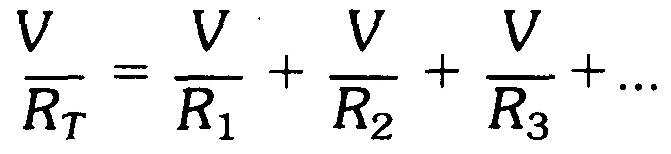
En divisant par V qui est le même pour toutes les résistances, on obtient:

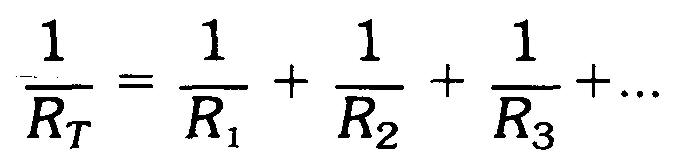    (4.3)

Cette formule des inverses s'applique à tout nombre de résistances en parallèle, quelle que soit leur valeur.

Utilisons les valeurs de la figure 4-7a comme exemple:

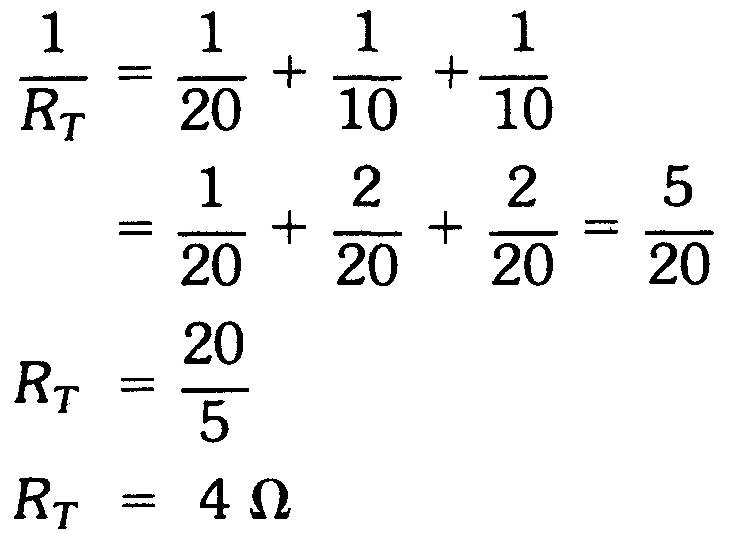
Remarquons qu'il faut inverser la valeur de I/R_T pour obtenir R_T si on utilise la formule 4.3.

Méthode du courant total

La figure 4-7b nous montre comment ce problème peut être résolu en partant du courant total au lieu de la formule des inverses, si on préfère ne pas utiliser les fractions.

Figure 4-7 Combinaison de résistances en parallèle en utilisant:

(a) la formule des résistances inverses; (b) la méthode du courant de ligne total On suppose une tension de ligne 20 V

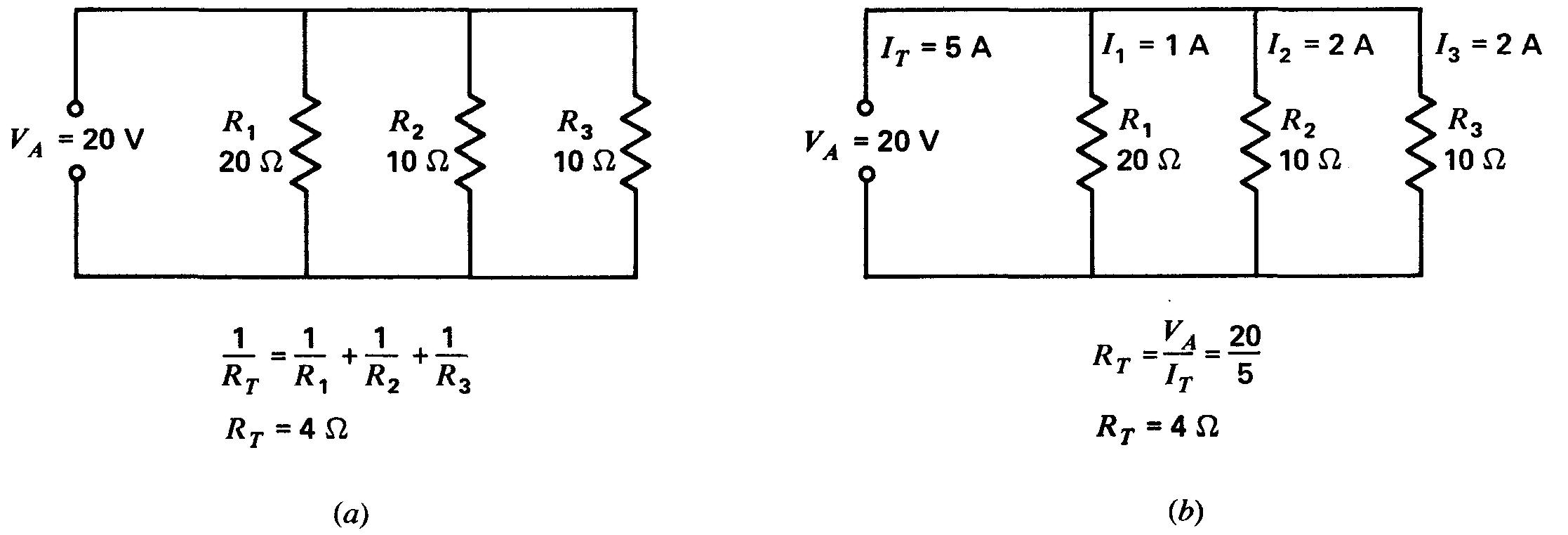
Bien que la tension appliquée ne soit pas toujours connue, on peut supposer une valeur quelconque car elle s'élimine dans les calculs.

En général, il est plus simple de supposer une tension appliquée ayant une valeur numérique égale à la résistance la plus élevée.

Dans ce cas, on suppose qu'un des courants de branches automatiquement égal à 1 A et les autres courants de branches, plus élevés, en éliminant les fractions inférieures à 1 dans les calculs.

À l'exemple de la figure 4-7b, la résistance la plus élevée est égale à 20 Ω.

Supposons une tension de 20 V, les courants de branches seront respectivement de 1, 2, et 2 A pour R1, R2 et R3.

Le courant de ligne total sera alors de 5 A.

La résistance combinée dans la ligne est de 20 V / 5 A, par conséquent égale à 4 Ω. Une valeur semblable est obtenue en utilisant la formule des inverses de résistances.

Cas particulier des résistances R égales dans toutes les branches

Si toutes les résistances en parallèle sont égales, la résistance combinée R_T est égale à la valeur d'une résistance de branche divisée par le nombre de branches.

Cette règle est illustrée par la figure 4-8 où trois résistances de 60 kΩ en parallèle sont égales à 20 kΩ.

Figure 4-8 Pour un nombre quelconque de résistances de branches égales, la résistance R_T est égale à la résistance R divisée par le nombre de branches. Ici, R_T vaut 20 kΩ.

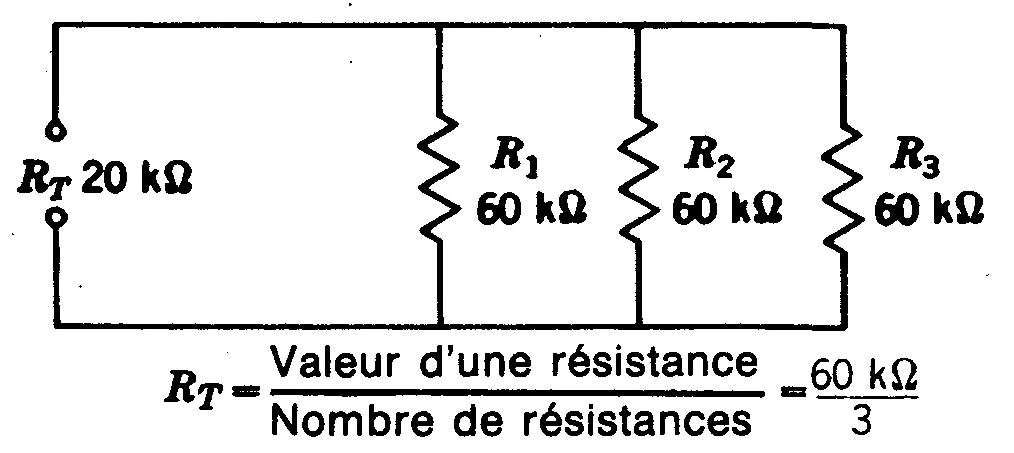
Cette règle s'applique à tout nombre de résistances en parallèle, pourvu qu'elles soient toutes égales.

Autre exemple:

cinq résistances de 60 Ω en parallèle ont une résistance combinée de 60/5 ou 12 Ω.

L'application ordinaire de ce cas particulier est le jeu de deux résistances R égales en parallèle, la résistance R_T valant la moitié de chaque R.

Cas particulier de deux branches

S'il y a seulement deux résistances en parallèle non égales, il est généralement plus rapide de calculer la résistance combinée en utilisant la méthode indiquée à la figure 4-9.

Figure 4-9 Pour deux résistances en parallèle quelconques, R_T est égal à leur produit divisé par la somme. Ici, R_T vaut 24 Ω.

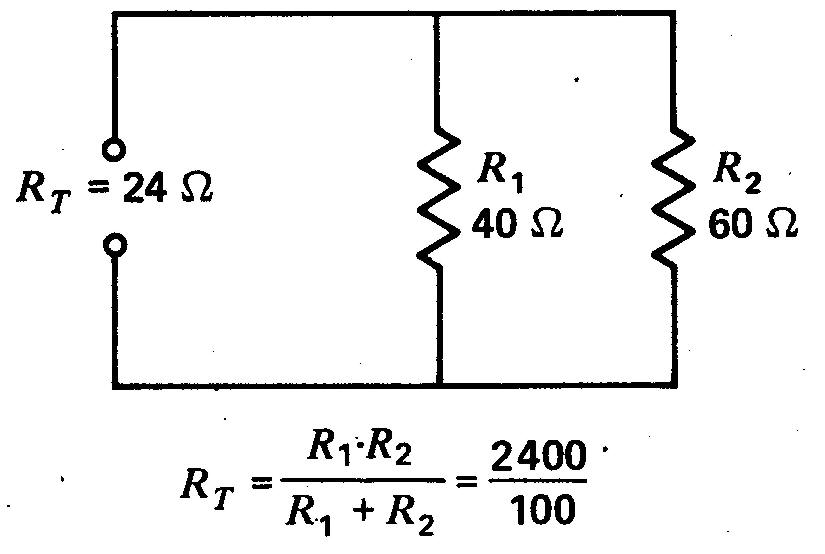
Cette règle indique que la combinaison de deux résistances en parallèle est leur produit divisé par leur somme:

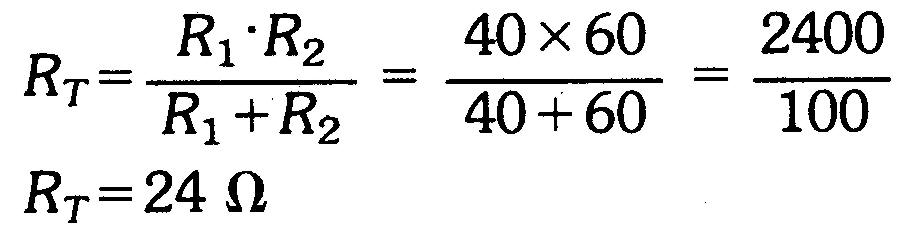
Les résistances peuvent avoir toutes les valeurs possibles à la condition qu'il n'y ait que deux résistances.

Remarquons que cette méthode donne directement R_T et non pas son inverse. Si on utilise la formule des inverses pour cet exemple, la réponse sera 1 / R_T = 1 / 24 qui est une valeur identique, R_T égalant 24 Ω.

Calculs simplifiés

La figure 4-10 montre de quelle façon ces calculs simplifiés peuvent aider à réduire les branches en parallèle en un circuit équivalent plus simple.

Figure 4-10 Exemple de calcul de résistances en parallèle:

(a) circuit comportant quatre branches; (b) combinaison en deux branches; (c)circuit équivalent réduit à une seule résistance R_T

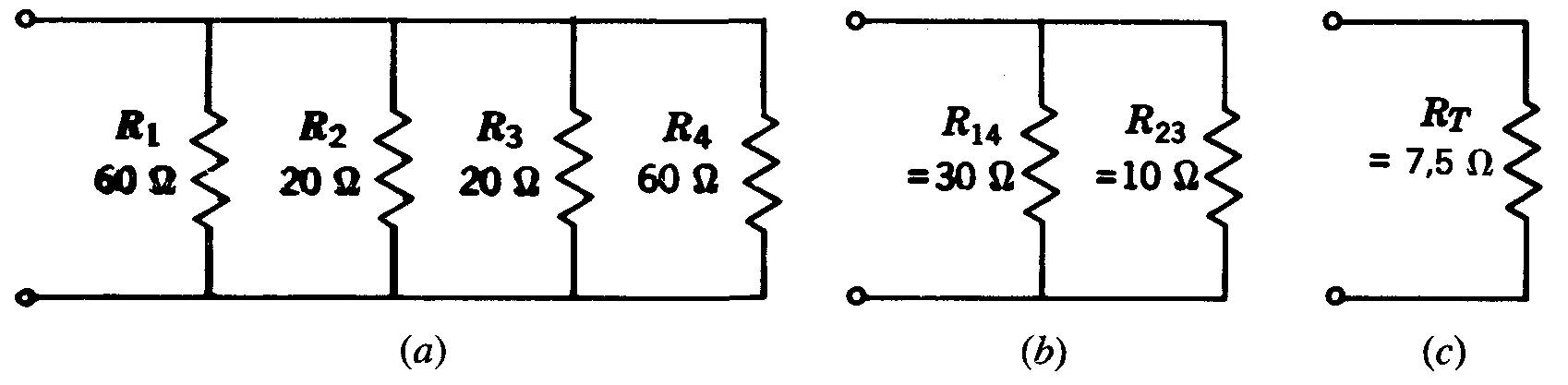
En (a), les résistances R1 et R4 de 60 Ω sont égales et en parallèle. Par conséquent, elles sont équivalentes à la résistance R14 de 30 Ω en (b).

De la même façon, les résistances R2 et R3 de 20 Ω sont équivalentes à la résistance R23 de 10 Ω.

Le circuit en (a) est équivalent au circuit plus simple en (b) avec seulement les deux résistances en parallèle de 30 Ω et 10 Ω.

Enfin, la résistance combinée pour ces deux dernières égale leur produit divisé par leur somme qui est 300 / 40 ou 7,5 Ω comme il est indiqué en (c). Cette valeur de R_T en (c) est équivalente à la combinaison des quatre branches en (a).

Si l'on connecte une source de tension sur l'un ou l'autre circuit, le courant du générateur dans la ligne principale sera le même dans les deux cas.

Pour déterminer R_T, l'ordre des connections pour les résistances en parallèle importe peu. La question de savoir quelle est la première ou la dernière ne se pose pas car elles sont toutes sur la même source de tension.

Calcul d'une résistance de branche inconnue Dans quelques cas, avec deux résistances en parallèle, il est utile de déterminer la valeur de R_X à connecter en parallèle avec une résistance R connue pour obtenir la valeur requise de R_T.

Les formules pourront être alors transposées comme indiqué ci-dessous:

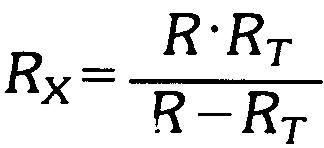    (4.5)

Exemple 5

Quelle est la résistance R_X à mettre en parallèle avec 40 Ω pour obtenir une résistance R_T de 24 Ω?

Réponse

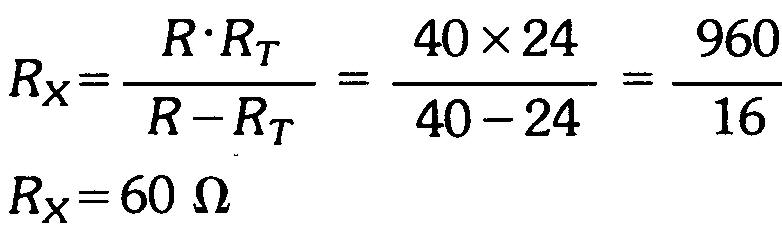
Ce problème correspond au circuit de la figure 4-9

Remarquer que la formule (4.5) de R_X est un produit sur une différence; R_T est soustrait, car c'est la plus petite résistance.

Exemple 6

Quelle résistance en parallèle avec 50 kΩ donnera une résistance R_T de 25 kΩ?

Réponse R = 50 kΩ

Deux résistances R égales en parallèle donnent une résistance R_T égale à la moitié de chaque R.

Problèmes pratiques (réponses à la fin du chapitre)

(a) Calculer la résistance équivalente R_T de trois résistances en parallèle égales chacune à 4,7 MΩ

(b) Soit deux résistances en parallèle de 3 MΩ et 2 MΩ. Calculer R_T.

4.5 CONDUCTANCES EN PARALLÈLE

Étant donné que la conductance G est égale à 1/R, la formule de l'inverse des résistances (4.3) peut être établie pour la conductance de la manière suivante:

GT = G1 + G2 + G3 + ... + Gn     (4.6)

R étant exprimé en ohms et G en siemens.

Pour l'exemple de la figure 4-11:

Figure 4-11 Pour obtenir la conductance totale GT, on additionne les conductances en parallèle.

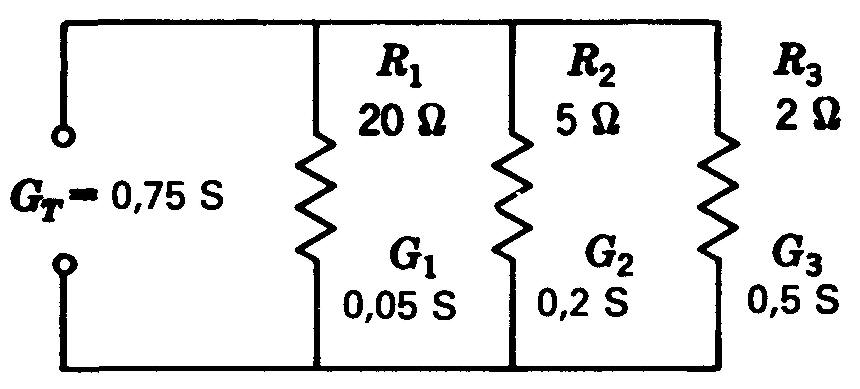
GT = 0,05 + 0,2 + 0,5 = 0,75S

Remarquons que le fait d'additionner les conductances n'exige pas d'inversions.

En fait, chaque valeur de G est l'inverse de R.

Dans certains circuits parallèle, il peut être plus facile de travailler avec des conductances plutôt qu'avec des résistances, afin d'éviter l'emploi de la formule des inverses pour R_T.

Le courant de chaque branche est directement proportionnel à la conductance de cette branche; cela correspond au fait que chaque chute de tension est directement proportionnelle à chaque résistance en série.

La raison pour laquelle les conductances en parallèle sont additionnées directement peut s'expliquer en supposant une source de 1 V appliquée à toutes les branches.

Le calcul des valeurs de 1/R pour les conductances est le même que celui des courants de branche. L'addition de ces valeurs donne I_T ou G_T.

Problèmes pratiques 4.5 (réponses à la fin du chapitre)

(a) Soit les conductances en parallèle G1 de 2 S et G2 de 5 S. Calculer G_T.

(b) Soit les conductances en parallèle G1 de 0,05 µS, G2 de 0,2 µS et G3 de 0,5 µS. Calculer G_T et R_T.

4.6 PUISSANCE TOTALE DANS LES CIRCUITS PARALLÈLE

Étant donné que la puissance dissipée dans les résistances de branche doit provenir de la source de tension, la puissance totale sera égale à la somme des valeurs individuelles de puissance dans chaque branche.

La figure 4-12 illustre cette règle. On peut également utiliser ce circuit pour savoir comment appliquer les règles du courant, de la tension et de la résistance dans un circuit parallèle.

Figure 4-12 La somme des puissances individuelles P1 et P2 utilisées dans chacune des résistances est égale à la puissance totale PT produite par la source.

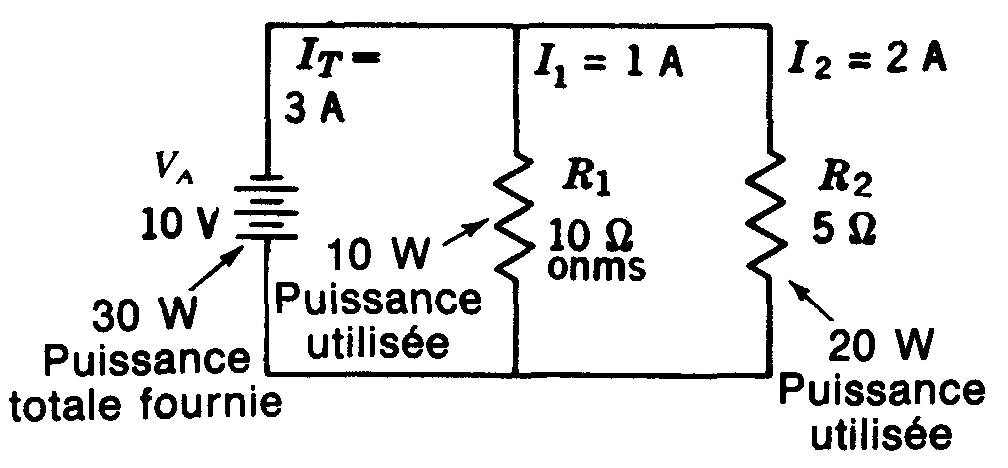
La tension de 10 V est appliquée aux bornes des résistances R1 (10 Ω) et R2 (5 Ω) de la figure 4-12. Le courant de branche I1 est alors V_A / R1 ou 10 / 10, soit 1 A.

De même, I2 vaut 10/5 ou 2 A. Le courant I_T total est 1+2 = 3 A.

Si l'on veut trouver la résistance R_T, elle est égale à V_A / I_T ou 10/3, soit 3,33 Ω.

La puissance dissipée dans chaque branche est V_A x I.

Dans la branche R1, le courant I1 = 1 A et la puissance P1 égale 10 x 1, ou 10 W.

Pour la branche R2, le courant I2 est égal à 2 A. Donc, P2 égale 2 x 10 = 20 W.

Si on additionne P1 et P2 on trouve 10 + 20 = 30 W pour P_T, ce qui est la puissance totale dissipée dans toutes les branches.

Cette valeur de 30 W pour P_T doit être égale à la puissance totale fournie par la source de tension en utilisant le courant total de ligne I_T.

En multipliant V_A par I_T, ou 10 par 3, on obtient 30 W pour P_T, égal à P1 + P2. Les 30 W de puissance fournis par la source sont dissipés dans les résistances de branche.

Remarquons que dans les arrangements série et parallèle, la somme des valeurs individuelles de puissance dissipées dans le circuit est égale à la puissance totale fournie par la source.

Cela s'exprime par la relation:

PT=P1 + P2 + P3 + ... Pn  (4.7)

Les arrangements de circuit série ou parallèle peuvent altérer la distribution de la tension ou du courant, mais la puissance est le régime auquel l'énergie est fournie. La disposition du circuit ne peut pas modifier le fait que toute l'énergie du circuit provient de la source.

Problèmes pratiques 4.6 (réponses à la fin du chapitre)

(a) Deux branches parallèle ont chacune 2 A sous 120 V. Calculer P_T.

(b) Trois branches parallèle de 10, 20 et 30 Ω sont soumises à une tension de 60 V. Calculer P_T.

4.7 ANALYSE DES CIRCUITS PARALLÈLE

II sera utile de se rappeler les points suivants pour résoudre les problèmes relatifs aux circuits parallèle:

1. La connaissance de la tension aux bornes d'une branche permet de déduire que cette tension se trouve aux bornes de toutes les branches. Il n'y a qu'une tension aux bornes des points de branche ayant la même différence potentielle.

2. Si on connaît I_T et l'un des courants de branche I1 on peut trouver I2 en le soustrayant de I_T.

Étant donné que I_T = I1 + I2, il est également vrai que I2 = I_T - I1 ou I1 = I_T - I2.

Le circuit de la figure 4-13 illustre ces points.

Figure 4-13 Analyse d'un circuit parallèle. Quelles sont les valeurs de Va et de R3? Se reporter au texte pour obtenir la solution.

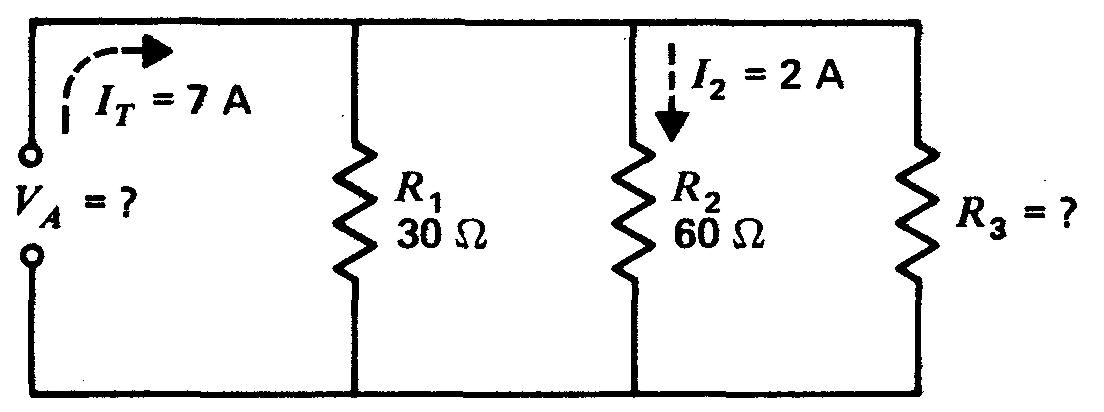
Le problème consiste à trouver la tension appliquée V_A et la valeur de R3. Sur les trois résistances de branche, on ne connaît que R1 et R2.

Toutefois, la valeur du courant I2 est de 2 A, la tension I2 x R2 doit être 2 x 60 ou 120 V.

La tension V_A appliquée n'est pas connue mais elle doit également être de 120 V, car la tension aux bornes de toutes les branches en parallèle est la même.

Par conséquent, on peut calculer I1 comme V_A / R1 ou 120 / 30, soit 4 A.

Étant donné que le courant I_T est de 7 A et que les deux branches consomment 2 + 4 ou 6 A, le courant de la troisième branche traversant la résistance R3 doit être 7 - 6 ou 1 A.

On peut alors calculer R3 comme V_A / I3, ce qui donne 120 / 1 ou 120 Ω.

Problèmes pratiques 4.7 (réponses à la fin du chapitre) Se reporter à la figure 4-13:

(a) Calculer V2 aux bornes de R2;

(b) Calculer I1 circulant dans R1

4.8 EFFETS D'UNE COUPURE SUR UN CIRCUIT PARALLÈLE

Une ouverture dans un circuit quelconque est une résistance infinie qui entraîne l'absence de courant.

Toutefois, dans des circuits parallèle, il existe une différence entre une ouverture de circuit dans la ligne principale et une ouverture de circuit dans une branche en parallèle.

La figure 4-14 est une illustration de ces deux cas.

Figure 4-14 Coupure de circuits parallèle:

(a) coupure de la ligne principale; aucun courant ne circule et les ampoules sont toutes éteintes;

(b) coupure dans une branche. L'ampoule 1 est éteinte, mais les deux autres ampoules fonctionnent normalement.

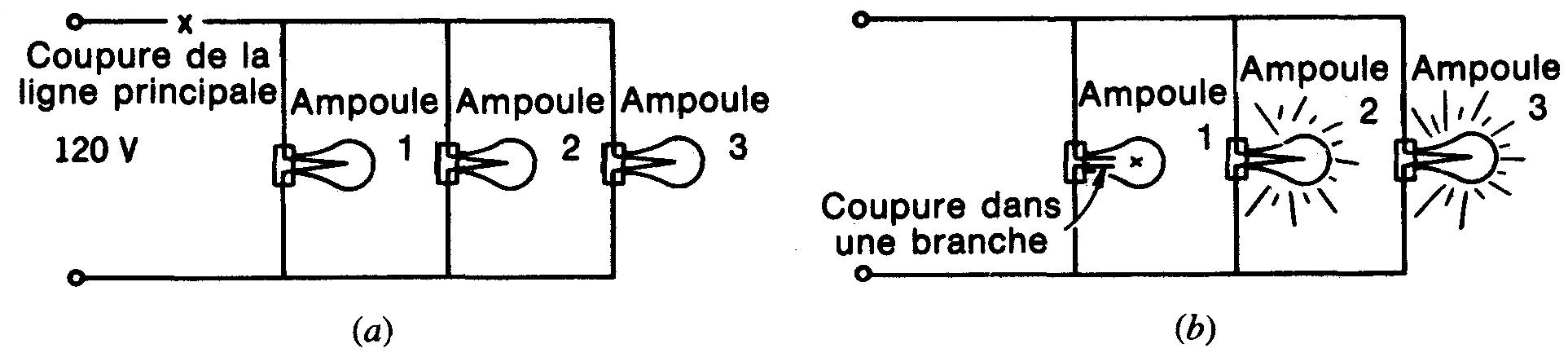
En (a), le circuit ouvert dans la ligne principale empêche toute circulation d'électrons dans la ligne vers l'ensemble des branches. Le courant est égal à zéro dans toutes les branches et, par conséquent, aucune lampe ne peut s'allumer.

Mais en (b), l'ouverture du circuit se trouve dans le circuit de branche de la lampe 1. Le circuit de branche ouvert n'a donc pas de courant et la lampe ne peut pas s'allumer.

Toutefois, le courant est normal dans toutes les autres branches en parallèle car chacune est reliée à la source de tension. Par conséquent, les autres lampes s'allument.

Le circuit de la figure 4-14b s'applique aux téléviseurs dont les filaments des tubes sont montés en parallèle. La coupure d'un filament n'empêchera pas le fonctionnement normal des autres. Un tel filament non chauffé au rouge est, ordinairement, facilement repérable.

Ces circuits démontrent l'avantage que représente le câblage des composants en parallèle. Une ouverture de circuit dans un composant n'affecte qu'une branche, et les autres branches en parallèle conservent leur tension et leur courant normaux.

Problèmes pratiques 4.8 (réponses à la fin du chapitre)

(a) Quelle est la valeur de résistance d'un filament coupé?

(b) Soit la figure 4-14b. Seule la branche de la lampe 3 est ouverte; quelle(s) ampoule(s) est (sont) allumée(s)?

4.9 EFFETS D'UN COURT-CIRCUIT AUX BORNES DES BRANCHES PARALLÈLE

Un court-circuit a pratiquement une résistance égale à zéro. Par conséquent, son effet se réduit à la production d'un courant excessif. Considérons l'exemple de la figure 4-15.

Figure 4-15 Un court-circuit aux bornes de l'une des branches en parallèle court-circuite toutes les branches.

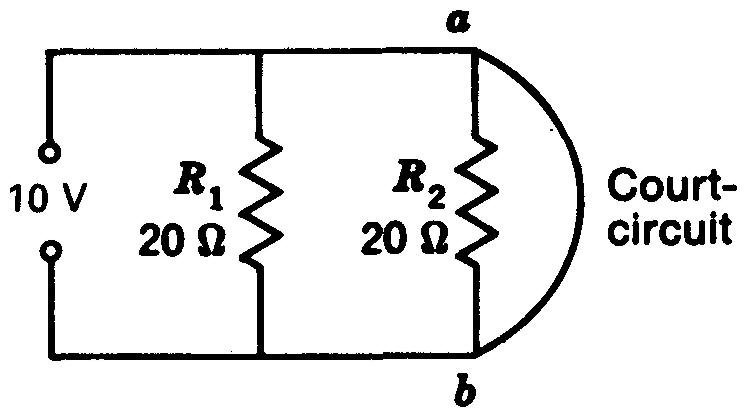
 Supposons que le fil conducteur au point a entre accidentellement en contact avec le fil au point b. Comme ce fil est un excellent conducteur, le court-circuit aboutit pratiquement à une résistance nulle entre les points a et b.

Ces deux points sont connectés directement aux bornes de la source de tension. Sans opposition, la tension appliquée pourrait fournir une valeur de courant infiniment élevée dans ce trajet de courant.

Courant de court-circuit Dans la pratique, le courant est limité par la faible résistance des fils et le fait que la source est habituellement incapable de conserver son courant de sortie tout en fournissant un courant excessif. Mais la valeur du courant peut être cependant dangereusement élevée.

Par exemple, le courant de court-circuit peut être de plusieurs centaines d'ampères au lieu du courant de ligne normal de 1 A illustré ici. Ce courant excessif est présent dans la source de tension, dans la ligne vers le point a, dans le court-circuit et dans la ligne revenant du point b.

En raison de cette grande valeur de courant, ces parties du circuit peuvent chauffer suffisamment pour prendre feu et brûler. Il y a donc lieu de disposer un fusible qui ouvrirait la ligne principale qui autrement serait, dans le cas d'un court-circuit d'une branche quelconque, parcourue par un courant trop élevé.

Aucun courant ne parcourt les composants court-circuités

Soit le court-circuit de la figure 4-15. Aucun courant ne traverse Ri et R2.

Étant donné que le court-circuit présente un trajet en parallèle avec une résistance pratiquement égale à zéro, tout le courant s'écoule par ce trajet, en dérivation des résistances.

Par conséquent, R1 et R2 sont en court-circuit et ne peuvent fonctionner sans leur courant normal. Par exemple, s'il y avait des résistances de filaments sur des ampoules d'éclairage, ces ampoules ne s'allumeraient pas car il ne passe aucun courant par les filaments.

Mais les composants en court-circuit ne subissent pas de dommage. Aucun courant ne les traverse. En supposant que le court-circuit n'a pas endommagé la source de tension et le câblage du circuit, ils ne peuvent fonctionner de nouveau lorsque le circuit est redevenu normal une fois le court-circuit supprimé.

Toutes les branches parallèle sont court-circuitées

S'il n'y avait qu'une résistance sur la figure 4-15 ou un nombre quelconque de résistances en parallèle additionnelles, elles seraient toutes court-circuitées du fait du court-circuit des points a et b.

Par conséquent, un court-circuit sur une branche dans un circuit parallèle met en court-circuit toutes les branches parallèles.
De même, un court-circuit sur la source de tension dans un circuit quelconque met en court-circuit le circuit tout entier.

Problèmes pratiques 4.9 (réponses à la fin du chapitre) Considérer la figure 4-15:

(a) Quelle est la valeur de la résistance du court-circuit entre les points a et b?

(b) Quelle est la valeur du courant Jx dans Ri avec un court-circuit entre les bornes de R2?

Résumé

1. Il n'existe qu'une tension VA sur tous les composants en parallèle.

2. Le courant dans chaque branche I_b est égal à la tension sur la branche VA divisée par la résistance de branche R_b, soit

I_b = V_A / R_b

3. Le courant de ligne total égale la somme de tous les courants dè branche, soit I_T = I1 +12 +13 +...

4. La résistance équivalente R_T des branches en parallèle est inférieure à la plus petite résistance de branche, car toutes les branches prennent plus de courant sur la source qu'une branche quelconque.

5. Pour seulement deux résistances en parallèle d'une valeur quelconque, R_T = R1R2 / (R1+R2).

6. Pour un nombre quelconque de résistances en parallèle égales R_T est la valeur d'une résistance divisée par le nombre de résistances.

7. Pour un nombre quelconque de branches, calculer R_T comme V_A / I_T, ou utiliser la formule des inverses de résistances.

8. Pour un nombre quelconque de conductances en parallèle, leur valeur s'additionne pour G_T, comme on additionne les courants des branches en parallèle.

9. La somme des valeurs de la puissance dissipée dans chacune des résistances en parallèle égale la puissance totale produite par la source, soit P_T = P1+P2 + P3 +...

10. Aucun courant ne circule dans une branche ouverte, mais les autres branches peuvent avoir leur courant normal. Toutefois, une ouverture dans une ligne principale donne un courant nul dans chacune de ces branches.

11. Un court-circuit a une résistance nulle, ce qui entraîne un courant excessif. Lorsqu'une branche est un court-circuit, tous les trajets en parallèle sont également en court-circuit. Le courant tout entier se trouve dans le court-circuit et dérive les branches en court-circuit.

Exercices de contrôle

(Réponses aux exercices de contrôle)

Voici un moyen de contrôler si vous avez bien assimilé le contenu de ce chapitre. Ces exercices sont uniquement destinés à vous évaluer vous-même.

Choisir (a), (b), (c) ou (d).

1. Si deux résistances sont reliées en parallèle:

(a) le courant passant par chacune d'elles doit être le même;

(b) la tension aux bornes de chacune d'elles doit être la même;

(c) leur résistance combinée égale la somme des valeurs individuelles;

(d) chacune doit avoir la même valeur de résistance.

2. Si 100 V sont appliqués sur 10 résistances de 50 Ω en parallèle, le courant pour chaque résistance est égal à:

(a) 2 A; (b) 10 A; (c) 50 A; (d) 100 A.

3. Si trois résistances de 1 kΩ sont reliées en parallèle, leur résistance équivalente est égale à:

(a)0,33 kΩ; (b) 1 kΩ; (c) 2 kΩ; (d) 3 kΩ.

4. Une résistance de 1 Ω en parallèle avec une résistance de 2 Ω fournit une résistance équivalente de:

(a) 3 Ω; (b) 1 Ω; (c) 2 Ω; (d) 0,67 Ω.

5. Avec des résistances de 100, 200, 300, 400 et 500 Ω en parallèle, R_T est:

(a) inférieure à 100 Ω; (b) supérieure à 1 MΩ; (c) de 500 Ω environ; (d) de 1 kΩ environ.

6. Si deux résistances sont reliées en parallèle, et si chacune d'entre elles dissipe 10 W, la puissance totale fournie par la source de tension est égale à:

(a) 5 W; (b) 10 W; (c) 20 W; (d) 100 W.

7. Si huit résistances de 10 MΩ, sont reliées en parallèle aux bornes d'une source de 10 V, le courant de la ligne principale est égal à:

(a) 0.1 µA; (b) 0,125 µA; (c) 8 µA; (d) 10 µA.

8. Un circuit parallèle ayant une tension de 20 V appliquée sur deux branches a un courant de ligne total de 5 A. La résistance d'une branche égale 5 Ω. La résistance de l'autre branche est égale à:

(a) 5 Ω; (b) 20 Ω; (c) 25 Ω; (d) 100 Ω.

9. Trois ampoules de 100 W sont connectées en parallèle sur le secteur à 120 V.

Si le filament de l'une des ampoules est coupé, combien d'ampoules pourront s'allumer?

(a) Aucune; (b) une; (c) deux; (d) toutes.

10. Si un circuit parallèle est ouvert dans la ligne principale, le courant:

(a) augmente dans chaque branche;

(b) est égal à zéro dans toutes les branches;

(c) est égal à zéro uniquement dans la branche qui a la résistance la plus élevée;

(d) augmente dans la branche qui a la résistance la plus basse.

Questions

1. Dessinez un schéma de câblage montrant trois résistances reliées en parallèle aux bornes d'une pile. Indiquez chaque branche et la ligne principale.

2. Citez deux règles s'appliquant aux valeurs de courant et de tension dans un circuit parallèle.

3. Expliquez brièvement pourquoi le courant est le même des deux côtés de la ligne principale qui relie la source de tension aux branches en parallèle.

4. (a) Montrez la manière de relier trois résistances égales pour obtenir une résistance équivalente égale au tiers de la valeur d'une résistance;

(b) montrez la manière dont on peut relier trois résistances égales pour obtenir une résistance équivalente représentant trois fois la valeur d'une résistance.

5. Pourquoi le courant dans des branches en parallèle peut-il être différent si elles ont toutes la même tension?

6. Pourquoi le courant augmente-t-il dans la source de tension tandis que l'on ajoute d'autres branches en parallèle au circuit?

7. Montrez la méthode algébrique pour tirer la formule R_T = R1R2 / (R1+R2) à partir de la formule des inverses pour deux résistances.

8. Tracez le schéma du circuit de cinq filaments de tubes à vide câblés en parallèle aux bornes d'une source alternative de 6,3 V.

9. Dites brièvement pourquoi la puissance totale est égale à la somme des valeurs individuelles de puissance, que l'on utilise un circuit en série ou un circuit parallèle.

10. Expliquez pourquoi un circuit ouvert dans la ligne principale invalide toutes les branches, alors qu'un circuit ouvert dans une branche affecte seulement le courant de cette branche.

11. Citez deux différences entre un circuit ouvert et un court-circuit.

12. Citez, par comparaison, toutes les différences possibles entre les circuits série et les circuits parallèle.

Problèmes

(Réponses aux problèmes de numéro impair)

1. Deux résistances R1 (15 Ω) et R2 (45 Ω) sont reliées en parallèle sur une batterie de 45 V.

(a) Dessiner le schéma,

(b) Quelle est la tension aux bornes de R1 et R2?

(c) Quel est le courant circulant dans R1 et R2?

(d) Quelle est l'intensité du courant de ligne principale?

(e) Calculer R_T.

2. Soit le circuit de la question 1; quelle est la puissance totale fournie par la batterie?

3. Un circuit parallèle a trois résistances de branche dont les valeurs sont respectivement 20, 10 et 5 Ω pour R1, R2 et R3. Le courant passant par la branche de 20 Ω est de 1 A.

(a) Dessiner le schéma

(b) Quelle est la tension appliquée sur toutes les branches?

(c) Trouver le courant passant par la branche de 10 Ω et la branche de 5 Ω.

4. (a) Dessiner le schéma d'un circuit parallèle avec trois résistances de branche, chacune soumise à une tension de 10 V et parcourue par un courant de branche de 2 A.

(b) Quelle est la valeur de I_T?

(c) Quelle est la valeur de R_T?

5. En nous référant à la figure 4-12, on suppose que R2 s'ouvre,

(a) Quelle est la valeur du courant dans la branche R2?

(b) Quelle est la valeur du courant dans la branche R1?

(c) Quelle est la valeur du courant de la ligne?

(d) Trouver la résistance totale du circuit,

(e) Trouver la puissance produite par la batterie.

6. Deux résistances R1 et R2 sont en parallèle aux bornes d'une source de 100 V. Le courant total de ligne est 10 A. Le courant I1 par R1 est de 4 A.

Dessiner un schéma du circuit en indiquant la valeur des courants I1 et I2 et les résistances R1 et R2 dans les deux branches.

Quelle est la résistance équivalente des deux branches sur la source de tension?

7. Trouver R_T pour les groupes suivants de résistance de branches:

(a) 10 Ω et 25 Ω;

(b) cinq résistances de 10 kΩ;

(c) deux résistances de 500 Ω;

(d) 100 Ω, 200 Ω et 300 Ω;

(e) deux résistances de 5 kΩ et deux de 2 kΩ;

(f) quatre résistances de 40 kΩ et deux résistances de 20 kΩ.

8. Quel est le nombre de Rx en parallèle à connecter sur une résistance de 100 kΩ pour ramener R_T à:

(a) 50 kΩ; (b) 25 kΩ; (c) 10 kΩ ?

9. Trouver la conductance totale en siemens, pour les branches suivantes:

G1 = 9000 µ; G2 = 7000 µS; G3 = 22000 µS.

10. En vous reportant à la figure 4-11, calculer R_T en combinant les résistances.

 Montrer que R_T est égal à 1/G_T si G_T est de 0,75 S.

11. Soit la figure 4-16. Calculer R3.

Figure 4-16

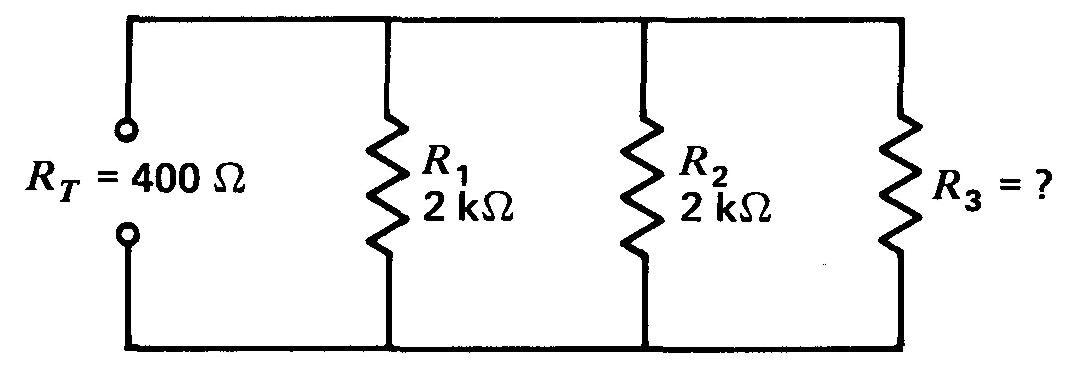
12. Soit la figure 4-17. Calculer:

Figure 4-17

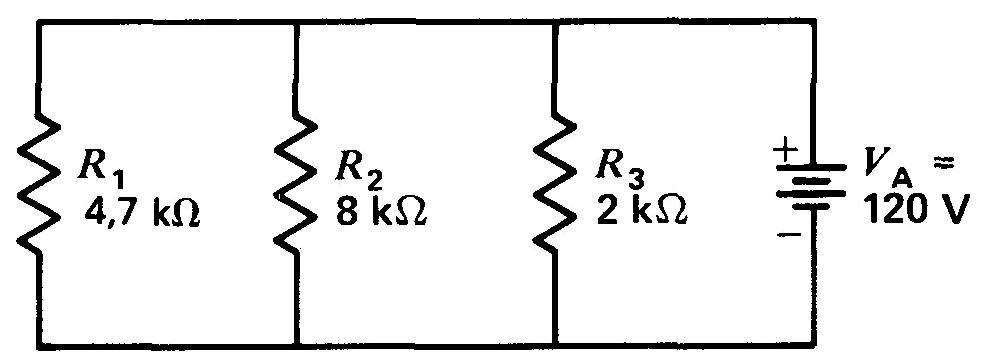
(a) le courant dans chaque branche et indiquer le sens de circulation des électrons;

(b) I_T; (c) R_T; (d) P1, P2, P3 et P_T

Réponses aux problèmes pratiques