Annexe D - Mathématiques

Mon premier cours en électronique

En utilisant les exposants dans les calculs, on peut gagner du temps lorsque l'on travaille sur des nombres très petits ou très grands, en particulier quand on travaille sur des capacités, en microfarads ou en picofarads.

De nombreux problèmes nécessitent aussi la transposition d'équations, l'élévation au carré d'un nombre ou l'extraction d'une racine carrée.

On explique ici comment faire ces opérations.

Enfin, on donne des notions de base en trigonométrie qui est l'étude des angles. On utilise la trigonométrie pour étudier les caractéristiques des courants et tensions alternatifs sinusoïdaux.

EXPOSANTS

On appelle exposant d'un nombre le nombre de fois où il est multiplié par lui-même:

10³ = 10 x 10 x 10=1000

Dans cet exemple, le nombre est 10.

L'exposant est 3, c'est-à-dire que le nombre est multiplié trois fois par lui-même.

L'exposant s'écrit sous forme d'un petit chiffre plus haut que le nombre lui-même. Il est la base.

Le nombre 10 est la base ordinaire dont on utilise les puissances.

On peut aussi dire «10 à la puissance trois».

Par exemple:

10⁰ = 1

10¹ = 10

10² = 10 x 10 = 100

10³ = 10 x 10x 10=1000

10⁴ = 10 x 10 x 10 x 10 = 10 000

10⁵ = 10 x1 0 x 10 x 10 x 10 = 100 000

10⁶ = 10 x 10 x 10 x 10 x 10 x 10 = 1000 000

Un nombre écrit sans exposant a en réalité l'exposant 1.

Par exemple, 10 et 10¹ sont identiques.

Quand un nombre n'a pas de virgule décimale, on suppose que cette virgule est après le dernier chiffre.

Pour le nombre 103, par exemple, la virgule décimale se trouve après le chiffre 3.

Lorsque des fractions décimales sont inférieures à 1, l'exposant est négatif.

Par exemple:

10^-1 = 0,1 = 1/10

10^-2 = 0,01 = 1/100

10^-3 = 0,001 = 1/1000

10^-4 = 0,0001 = 1/10 000

10^-5 = 0,000 01 = 1/100 000

10^-6 = 0,000 001 = 1/1 000 000

On doit se souvenir des puissances positives de 10 jusqu'à un million et négatives de 10 jusqu'à un millionième, car elles aident à simplifier les calculs dans notre système de numération décimale.

TRANSFORMATION EN PUISSANCES DE 10

Quand un nombre n'est pas égal à un nombre entier de dizaines, de centaines, de milliers, etc., on peut le mettre sous forme d'un produit de deux facteurs de façon à utiliser une puissance de dix.

En voici des exemples:

10 = 1 x 10= 1 x 10¹

20 = 2 x 10 = 2 x 10¹

75 = 7,5 x 10 = 7,5 x 10¹

98 = 9,8 x 10 = 9,8 x 10¹

100 = 1 x 100 = 1 x 10²

750 = 7,5 xl 00 = 7,5 x 10²

980 = 9,8 x 100 = 9,8 x1 0²

1000 = 1 x 1000 = 1 x 10³

7500 = 7,5 x 1000 = 7,5 x 10³

9000 = 9 x 1000 = 9 x 10³

9830 = 9,83 x 1000 = 9,83 x 10³

On remarque que l'exposant est égal au nombre de rangs dont on a décalé la virgule décimale vers la gauche.

Par exemple, dans 980 = 9,8 x 10², l'exposant est 2, car la virgule décimale a été décalée de deux rangs quand on est passé de 980 au facteur 9,8 que multiplie 10².

La même idée s'applique aux fractions inférieures à 1, mais cette fois l'exposant négatif est le nombre de rangs dont on a décalé la virgule décimale vers la droite.

En voici quelques exemples:

0,01 =1 x 0,01 = 1 x 10^-2

0,02 = 2  x0,01 =2 x 10^-2

0,05 =5 x 0,01 = 5 x 10^-2

0,09 =9 x 0,01 =9 x 10^-2

0,093 = 9,3 x 0,01 = 9,3 x 10^-2

On remarquera que, dans un nombre comme 9 x 10³, le 9 est le facteur ou coefficient à multiplier par la puissance de la base.

Dans ce cas, 9 est multiplié par 10³ ou 1000 et le produit est égal à 9000.

Quand il n'y a pas de coefficient, on suppose que le coefficient est 1.

Ainsi, 1000 peut s'écrire 1 x 10³ ou simplement 10³.

Les nombres supérieurs à 1 s'écrivent toujours avec une puissance positive de 10.

Les fractions décimales inférieures à 1 ont toujours une puissance négative de 10.

En outre, l'exposant est le nombre de rangs dont on a décalé la virgule décimale quand on a introduit une puissance de dix.

En déplaçant la virgule décimale vers la gauche, on abaisse la valeur numérique, ce qui correspond à une division. Il faut donc élever l'exposant positif pour conserver le même nombre.

Ainsi: 123 et 1,23 x 10² sont égaux.

Dans le cas opposé, le déplacement de la virgule décimale vers la droite augmente la valeur numérique et correspond à une multiplication.

Il faut donc diminuer un exposant positif ou augmenter un exposant négatif pour conserver la même valeur.

Ainsi: 0,002, 0,2 x 10^-2 et 2 x 10^-3 sont égaux.

De même, 9,83 x 10³ est égal à 98,3 x 10², qui sont tous deux égaux à 9830.

On peut trouver, par les méthodes qui suivent, de combien de rangs il faut décaler la virgule décimale.

Quand on introduit des puissances de 10, pour poser les calculs d'un problème, on choisit un coefficient de la puissance de 10 ayant une valeur comprise entre 1 et 10.

Par exemple, on écrit 9830 sous la forme 9,83 x 10³.

Cette forme a l'avantage de conduire à une détermination plus facile de la position de la virgule décimale dans le résultat final, quand tous les nombres sont mis sous cette forme.

Un autre avantage de cette forme, c'est que la puissance de 10 est alors la partie principale du logarithme décimal du nombre.

Cependant, dans le résultat final d'un problème, il est préférable d'avoir un exposant de 10 qui soit multiple de 3 ou de 6 pour utiliser les multiples ou sous-multiples des unités.

Par exemple, un résultat de 42 x 10^-3 A indique qu'il s'agit de 42 m A,

alors que cela est moins évident sous la forme 4,2 x 10^-2.

On remarque que ces deux valeurs sont égales à 0,042 A.

OPÉRATIONS SUR LES PUISSANCES

Les puissances de 10 sont commodes pour multiplier ou diviser des nombres qui sont très grands ou très petits, car l'opération se ramène à une addition ou à une soustraction des exposants.

Règle 1

Pour multiplier des puissances de la base 10, on additionne leurs exposants.

Par exemple:

(1 x 10⁴) x ( 1 x 10²) = 1 x 10⁶

ou

10 000 x 100 =1 000 000

On remarque, cependant, que seuls les exposants de 10 s'additionnent. Les autres facteurs se multiplient toujours.

Ici, 1 x 1 est toujours égal à 1.

Voici un exemple des autres facteurs:

(2 x 10⁴) x ( 3 x 10²) = 6 x 10⁶

ou

20 000 x 300 = 6 000 000

Quand ce sont des exposants négatifs, on les additionne pour obtenir un nombre négatif plus grand:

(1 x 10^-2) x (1 x 10^-1) = 1 x 10^-3

ou

0,01 x 0,1 = 0,001

Dans le cas où il y a à la fois un exposant positif et un exposant négatif, on fait la différence entre les deux et on lui donne le signe du plus grand exposant:

(1 x 10⁵) x (1 x 10^-3) = 1 x 10²

(1 x 10^-5) x (1 x 10³) = 1 x 10^-2

Règle 2

Pour diviser des puissances de 10, on soustrait les exposants.

Par exemple:

(1 x 10⁶) / (1 x 10³) = 1 x 10³

1 000 000- 1 000 =1 000

Seuls les exposants de 10 ont été soustraits.

Les autres facteurs se divisent toujours:

6 000 000 / 3 000 = 2 000

Lorsque le diviseur a un exposant négatif, on change son signe et on l'additionne.

Par exemple:

(1 x 10⁵) / (1 x 10^-3) = 1 x 10⁸

(1 x 10^-5) / (1 x 10³) = 1 x 10^-2

Le cas où le numérateur et le dénominateur d'une division sont égaux est intéressant Le quotient doit alors être égal à 1.

Par exemple:

1 x 10⁴ / 1 x 10⁴= 1 x 10⁰ = 1 x 1 = 1

Cet exemple montre que, pour une base quelconque, la puissance zéro du nombre est égale à 1, car l'exposant zéro correspond à une fraction dont le numérateur et le dénominateur sont égaux.

Par exemple:

2⁰ = 5⁰ = 125⁰ = 100⁰ = 1

Règle 3

Pour additionner ou soustraire des nombres exprimés avec des puissances de 10, les puissances doivent être les mêmes.

On additionne ou on soustrait alors les coefficients en conservant la même puissance de 10.

Par exemple:

(6 x 10³) + (2 x 10³) = 8 x 10³

(6 x 10³) - (2 x 10³) = 4 x 10³

Si les nombres ne sont pas exprimés avec la même puissance de 10, il faut les transformer pour avoir la même puissance de 10, avant de pouvoir les additionner ou les retrancher.

On peut utiliser une puissance quelconque pourvu que ce soit la même pour les deux nombres.

Règle 4

Pour élever une puissance à une puissance plus élevée, on multiplie les exposants.

Par exemple:

(2 x 10²)³ = 2³ x 10⁶ = 8 x 10⁶

On remarque que le coefficient 2 est élevé à la puissance indiquée.

Règle 5

Pour prendre la racine d'une puissance, on divise l'exposant par l'ordre de la racine.

Par exemple:

On remarque que l'on prend la racine indiquée du coefficient car:

On peut aussi exprimer une racine sous forme d'une puissance fractionnaire.

La racine cubique est identique à la puissance 1/3 et la racine carrée est identique à la puissance 1/2.

On peut appliquer la règle 4 aux puissances fractionnaires.

Par exemple, l'exposant 6 divisé par 3 est le même que 6 x 1/3.

FRACTIONS DÉCIMALES

Dans les calculs, il est souvent nécessaire de mettre une fraction sous forme décimale. C'est dans ce but que l'on devra se souvenir des conversions suivantes:

1/2 = 0,5

1/3 = 0,333

1/4 = 0,25

1/5 = 0,2

1/6 = 0,167

1/7 = 0,143

1/8 = 0,125

1/9 = 0,111

Ces fractions sont les inverses des chiffres 2 à 9.

On notera aussi que 1/1 = 1, que 0/1 =0, et que 1/0 est infini.

CARRÉS ET RACINES CARRÉES

La puissance 2 d'un nombre indique que ce nombre est élevé au carré.

Par exemple, 10² équivaut à 100, ou 100 est le carré de 10.

Le carré est donc égal au nombre multiplié par lui-même.

Par exemple, 6² est égal à 6 x 6 ou 36.

Dans l'opération inverse, la racine carrée d'un nombre est le nombre qui, multiplié par lui-même, redonne le premier nombre.

La racine carrée de 36, par exemple, est égale à 6, ce qui peut s'écrire V36 ou (36)^1/2 = 6.

Le signe V signifie racine carrée de.

Les carrés et les racines carrées sont indiqués au tableau D-1.

Tout nombre de la colonne N a son carré dans la colonne N2 et sa racine carrée dans la colonne VN

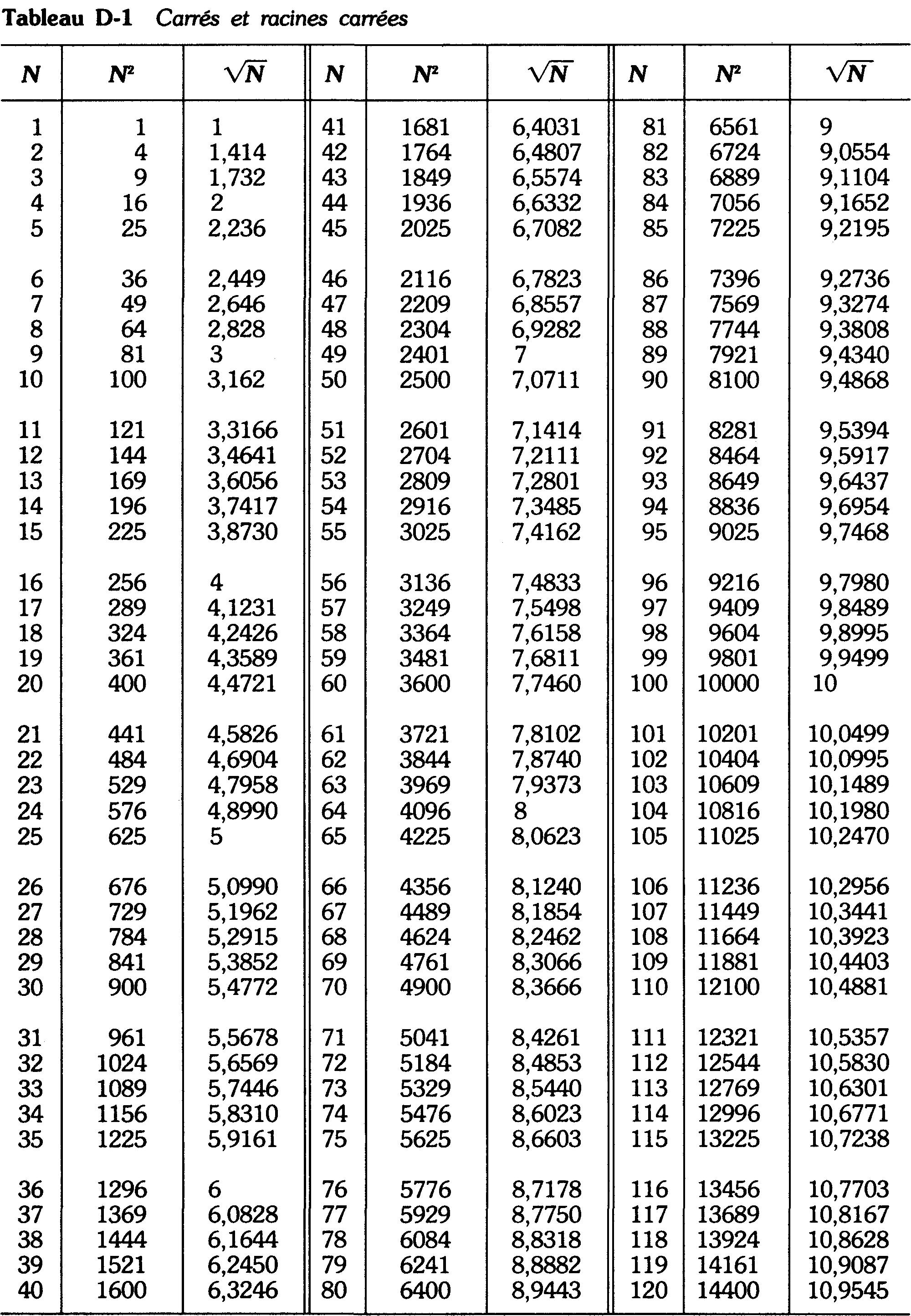
Ce tableau ne concerne que les nombres inférieurs ou égaux à 120.

Quand on a des nombres plus grands, il faut les décomposer; en facteurs plus petits.

Par exemple

V300 = V3 x V100 = 1,732 x 10 = 17,32.

On peut aussi utiliser la calculatrice électronique pour trouver les carrés et les racines carrées d'un nombre quelconque.

TRANSPOSITION DES ÉQUATIONS

Dans beaucoup d'applications, il faut transposer une équation algébrique avant de pouvoir faire le problème.

Les trois formes de la loi d'Ohm ne sont que des transpositions de V=IR, I=V/R, ou R = V/I.

On peut réaliser une transposition en utilisant la méthode suivante.

En considérant que l'on ne modifie pas une égalité en multipliant ou en divisant ses deux membres par un même nombre, on peut éliminer certaines quantités dans un membre pour obtenir l'équation désirée en utilisant un facteur approprié.

Si on suppose, par exemple, que l'on désire faire une transposition de l'équation V = IR pour obtenir une expression de I, l'idée consiste à diviser les deux membres par R pour qu'il s'élimine du terme IR:

V = IR

En divisant par R, on a:

V / R = IR / R

V/R = I ou I = V/R

Que I se trouve dans le premier ou dans le second nombre n'importe pas, car l'égalité est vraie dans les deux sens.

Comme autre exemple, on suppose que l'on transforme la formule X_L = 2πfL pour isoler L, d'un côté.

Pour y parvenir on divise les deux membres par 2πf.

La méthode est la suivante:

X_L = 2πfL

En divisant par 2πf, il devient:

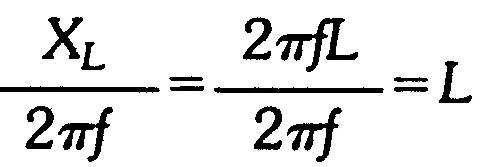
ou

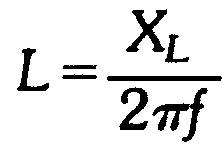
Cette méthode de multiplication des deux membres par un facteur qui s'élimine peut s'appliquer à toutes les équations.

TRIGONOMÉTRIE

La trigonométrie est l'étude des angles qui est très importante pour les déphasages du courant alternatif ou de la tension alternative.

Les angles sont nécessaires pour définir les mouvements circulaires.

Comme on l'indique à la figure D-1, si la ligne OP₁ est articulée à l'origine et qu'elle tourne jusqu'à P₂,

elle balaie l'angle P₁OP₂..

Figure D-1 Formation d'un angle φ.

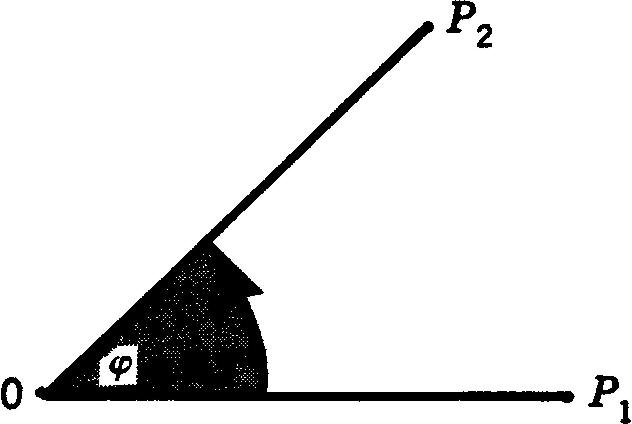
 Le symbole d'un angle est généralement φ.

Par convention, φ est positif quand la rotation se fait dans le sens inverse des aiguilles d'une montre, et négatif quand la rotation se fait dans le sens des aiguilles d'une montre.

Un angle droit, égal à 90°, a ses côtés perpendiculaires.

Les angles inférieurs à 90° sont aigus, les angles supérieurs à 90° sont obtus.

Un tour complet de la circonférence correspond à un angle de 360°.

Une rotation d'un degré est 1/360 du cercle complet.

On peut diviser un angle inférieur à 1° en parties décimales.

Par exemple, 0,5° est la moitié d'un degré; 26,5° est la moyenne arithmétique entre 26 et 27°.

Ce procédé est la notation trigonométrique décimale.

On peut aussi subdiviser 1° en 60 minutes et 1 minute en 60 secondes.

Cette méthode est la notation sexagésimale.

Par exemple, 26°30'0", ou 26 degrés, 30 minutes, et zéro seconde sont des angles égaux à 26,5°.

LE TRIANGLE RECTANGLE

Comme on le montre à la figure D-2, ce triangle a un angle droit.

Figure D-2 Le triangle rectangle.

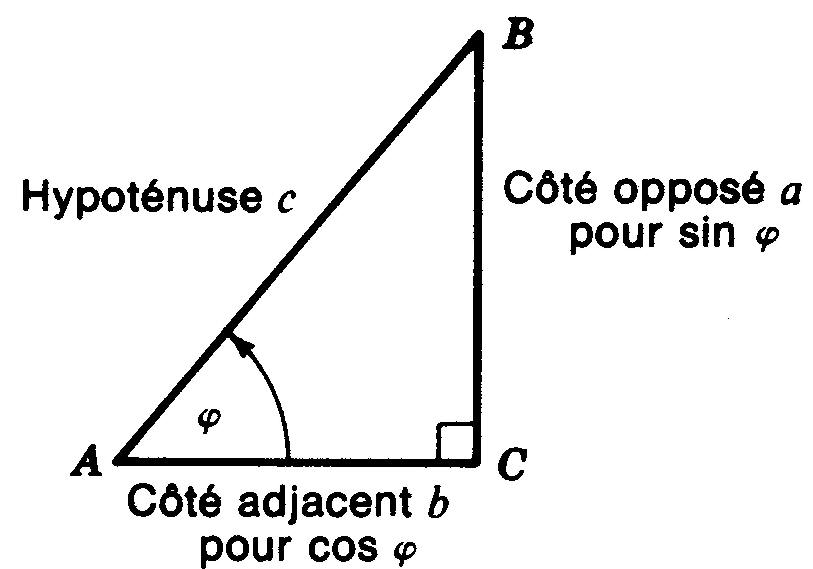
Le côté opposé à l'angle droit est l'hypoténuse.

Le côté vertical est en général désigné par a, qui signifie altitude, et le côté horizontal par b, qui signifie base; c est l'hypoténuse.

D'après le théorème de Pythagore:

L'hypoténuse c doit être supérieure à chacun des côtés de l'angle droit, mais inférieure à leur somme a + b.

FONCTIONS TRIGONOMÉTRIQUES

On les utilise pour définir les caractéristiques d'un angle.

Les six fonctions sont le sinus, le cosinus, la tangente, la cotangente, la sécante et la cosécante.

On ne définit ici que sin φ, cos φ, et tg φ, car ce sont les fonctions plus couramment employées dans les circuits alternatifs.

Les définitions sont basées sur le triangle rectangle de la figure D-2, et sont:

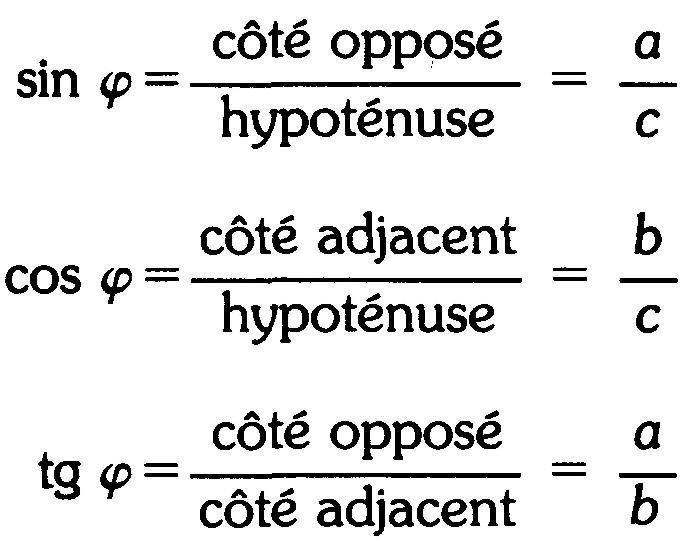
On considère que b est adjacent à φ, car c'est un côté de l'angle.

Un côté opposé ne fait pas partie de l'angle.

L'hypoténuse est toujours opposée à l'angle droit.

Il peut être intéressant de remarquer que les trois autres fonctions sont les inverses des premières,

car cotg φ = 1/tg φ, sec φ = 1/cos φ et cosec φ = 1/sin φ.

Une fonction trigonométrique est un nombre pur sans unité puisque c'est le rapport de deux grandeurs, bien que l'angle se mesure en degrés.

Par exemple, pour φ = 45°, sin φ = 0,707, qui est égal au rapport aie.

La taille du triangle n'intervient pas, car les rapports des côtés sont toujours les mêmes pour un angle donné.

Les fonctions trigonométriques définissent donc l'angle.

On peut obtenir les valeurs numériques à partir d'un tableau comme le tableau D-2 ou en utilisant une calculatrice électronique.

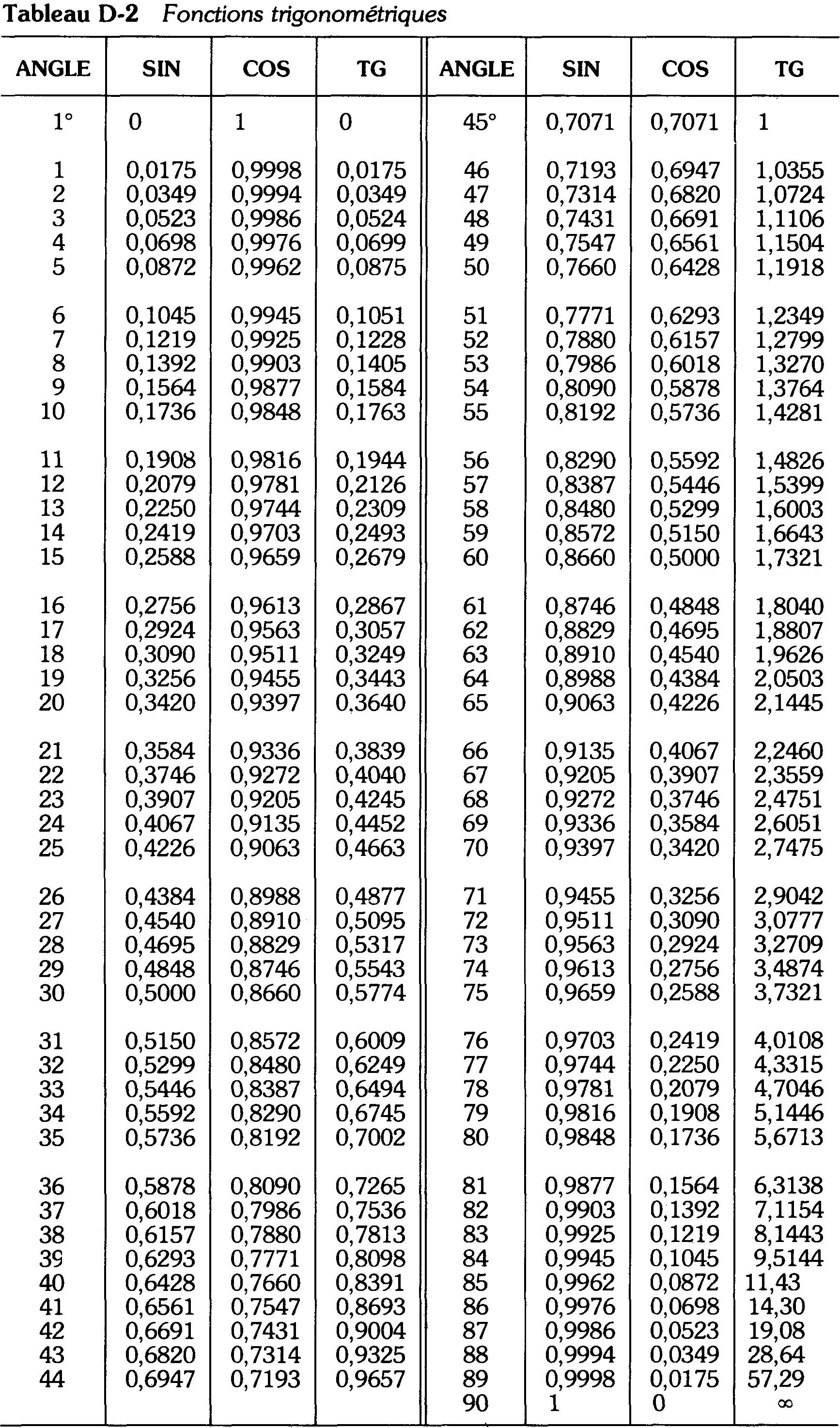
La valeur du sinus est 0 pour 0°, elle augmente jusqu'à un maximum de 1, pour 90°.

Ces valeurs s'expliquent parce que l'hypoténuse c est le plus grand côté et que le rapport a/b ne peut atteindre, au maximum, que 1/1.

Le cosinus, au contraire, a son maximum de 1 pour 0° puis il décroît jusqu'à 0 pour 90°.

La tangente augmente avec l'angle, depuis 0 pour 0°, jusqu'à 1 pour un angle de 45° qui correspond à un triangle rectangle isocèle dont le rapport des côtés est égal à 1.

Pour les angles plus grands que 45°, les tangentes sont supérieures à 1.

Pour utiliser le tableau, il suffit de chercher l'angle dans la première colonne et de trouver la valeur correspondante du sinus, du cosinus ou de la tangente.

Par exemple, sin 30° = 0,5; cos 30° = 0,866; tg 30° = 0,5774.

On peut aussi opérer à l'envers en trouvant l'angle dont on connaît une fonction.

Si, par exemple, sin φ = 0,7071, l'angle est de 45°.

ANGLES SUPÉRIEURS À 90°

Les angles considérés jusqu'à maintenant ne dépassaient pas 90°.

Pour des angles plus grands, allant jusqu'à 360°, on divise tout le cercle en quatre quadrants,
comme on l'indique à la figure D-3.

Figure D-3 Les quatre quadrants d'un cercle.

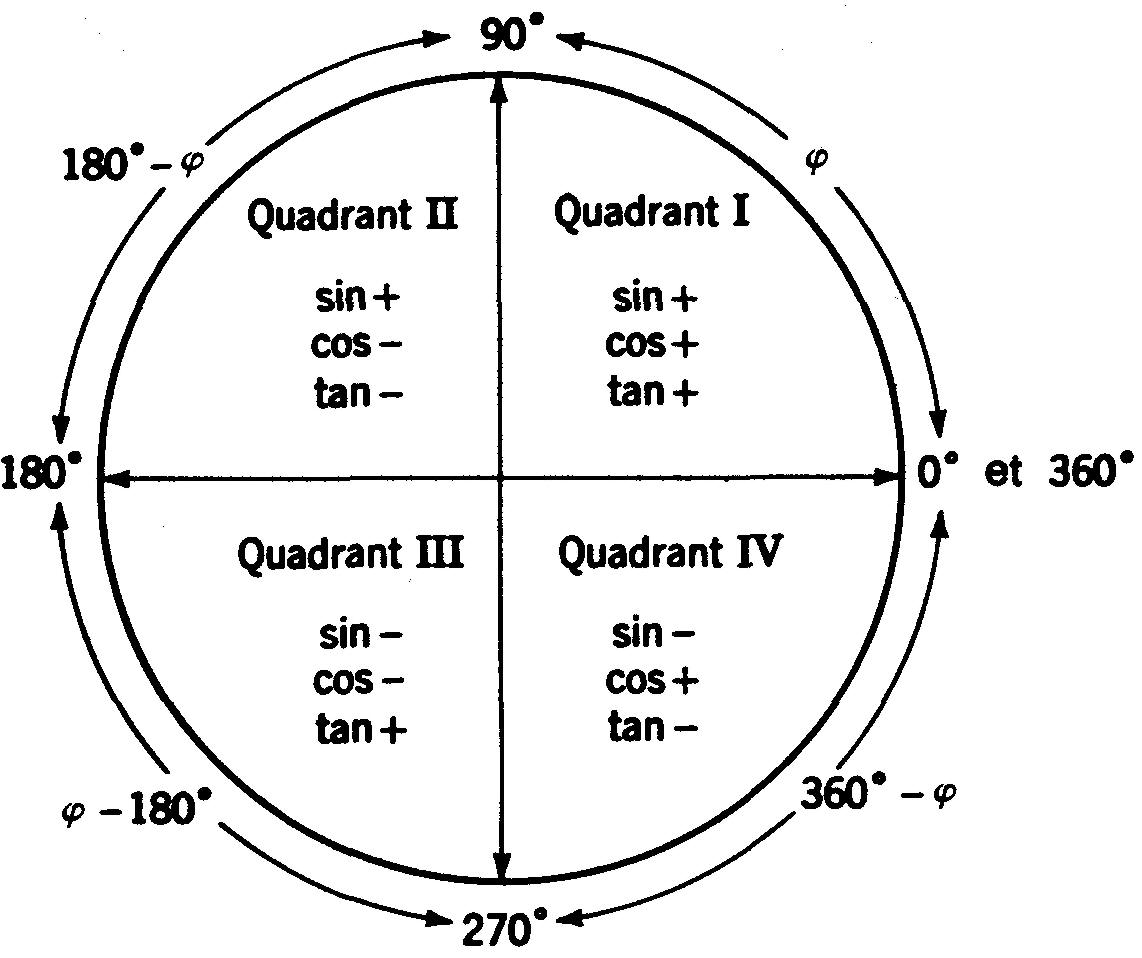
Pour utiliser le tableau des fonctions trigonométriques dans le cas où les angles sont obtus et appartiennent aux quadrants II, III et IV, on cherche les angles aigus du quadrant I qui ont des fonctions de même valeur par les règles suivantes:

pour le quadrant II, utiliser 180° - φ;

pour le quadrant III, utiliser φ -180°;

pour le quadrant IV, utiliser 360° - φ.

On tiendra également compte du signe et de la polarité des fonctions trigonométriques des différents quadrants, comme on l'indique à la figure D-3.

Par exemple:

Dans le quadrant II:

tg 120°= -tg (180°-120°)= -tg 60° = -1,7321

Dans le quadrant III:

tg 210° = tg (210° -180°) = tg 30° = 0,5774

Dans le quadrant IV:

tg 300° = - tg (360° - 300°) = - tg 60° = -1,7321

On remarque que les transformations reviennent à utiliser comme références l'axe horizontal, soit dans le sens 180°, soit dans le sens 360°.

Dans le premier quadrant, toutes les fonctions sont positives.

On remarque que la polarité de la tangente alterne dans les quadrants I, II, III et IV.

Pour tous les quadrants, le sinus a le signe positif ( + ) quand l'ordonnée est positive et le signe négatif ( - ) quand l'ordonnée est négative.

De même, le cosinus a le signe + quand l'abscisse horizontale est à droite ou le signe - quand elle est à gauche.

L'hypoténuse n'a pas de polarité.

Enfin, la tangente a le signe + quand le sinus et le cosinus ont la même polarité, soit + pour le quadrant I, soit - pour le quadrant III.

Pour plus de détails sur la trigonométrie et les mathématiques, on pourra consulter la sélection d'ouvrages indiquée en bibliographie.