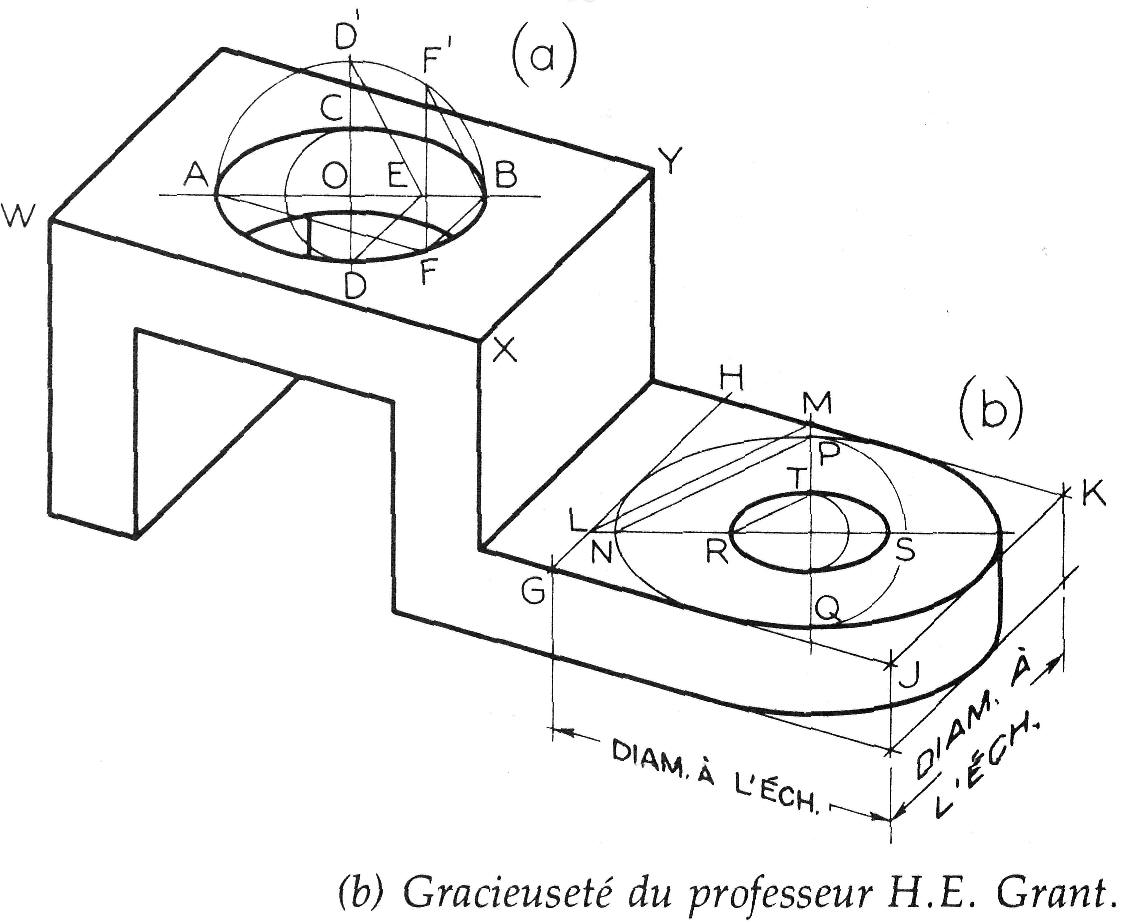
Figure 16.47
Ellipses en perspective trimétrique
Ellipses en perspective trimétrique
Les axes de symétrie d'un cercle deviennent les axes conjugués de l'ellipse correspondante en projection trimétrique. On peut alors tracer l'ellipse par une des méthodes illustrées aux figures 4.51, 4.52.b, 4.53.C, 4.48, 4.49 ou 4.52.a, ou simplement à l'aide d'un gabarit (figure 4.55) section Construction d'une ellipse dans Tracés géométriques.
A cause du nombre illimité de positions possibles pour une projection trimétrique, la variété des ellipses est infinie, ce qui peut devenir un facteur décourageant pour le dessinateur. On peut néanmoins observer quelques règles de base:
1. Sur le dessin, le grand axe de l'ellipse est toujours perpendiculaire à l'axe de symétrie du cylindre.
2. Le petit axe est toujours perpendiculaire au grand axe et, du même fait, il est confondu à l'axe de symétrie du cylindre.
3. La longueur du grand axe est égale au diamètre réel du cylindre.
Par conséquent, on connaît toujours, a priori, les directions des axes orthogonaux de l'ellipse ainsi que la longueur du grand axe.
Par contre, la longueur du petit axe est inconnue. Pour la déterminer, on peut utiliser une des deux méthodes suivantes.
À la figure 16.47.a, on connaît la direction du grand axe et sa longueur AB.

Figure 16.47
Ellipses en perspective trimétrique
Dans ce cas-ci, AB est horizontal puisque l'axe du cylindre est vertical.
De A et de B, on trace des parallèles aux arêtes axonométriques WX et XY respectivement, de façon à obtenir leur point d'intersection F qui est un point de l'ellipse à tracer.
De F, on élève une verticale pour déterminer F' sur le demi-cercle de diamètre AB. De D', le prolongement du petit axe sur le demi-cercle, on trace D'E parallèle à F'B. La ligne ED, qui est parallèle à BF, coupe le petit axe au point D.
Ce point est une extrémité du petit axe de l'ellipse à tracer. Par symétrie, on trouve l'autre extrémité C. A partir des deux axes maintenant connus, AB et CD, on utilise une des méthodes de construction expliquées à la section Construction d'une ellipse dans Tracés géométriques pour tracer l'ellipse.
Lorsque le parallélogramme capable de l'ellipse est connu ou facilement déterminable, on peut utiliser une deuxième méthode (figure 16.47.b.) pour trouver les extrémités de l'ellipse.
La direction des axes étant connue d'avance, on trace LM. La longueur du grand axe étant connu, on connaît donc N, et on trace NP parallèle à LM pour déterminer P, qui est une extrémité du petit axe cherché. D'autre part, si l'on veut trouver le petit axe de la petite ellipse, il suffit de tracer RT parallèle à LM ou à NP.
Pour construire une ellipse située sur un plan oblique dans une perspective
trimétrique, on applique une méthode semblable à celle utilisée pour les
perspectives isométriques (figure 16.33 section
Intersections).
