Inductance

Électrotechnique

Dans cette section, nous étudierons une des propriétés les plus importantes des enroulements. Cette propriété, appelée inductance, permet d'évaluer les tensions induites dans les bobines de même que la quantité d'énergie qu'elles emmagasinent.

L'inductance joue un rôle important dans les circuits à courant continu et à courant alternatif, si bien que tous les domaines de l'électrotechnique sont affectés par cette propriété de base.

Cette section mérite donc une attention toute particulière.

Inductance mutuelle - le henry

Considérons deux bobines A et B plus ou moins rapprochées (Fig. 19-1).

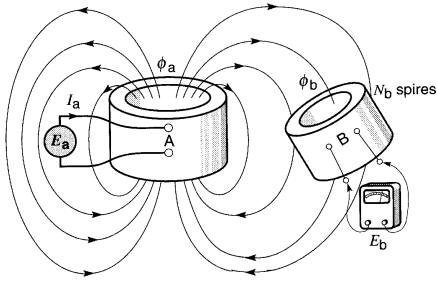
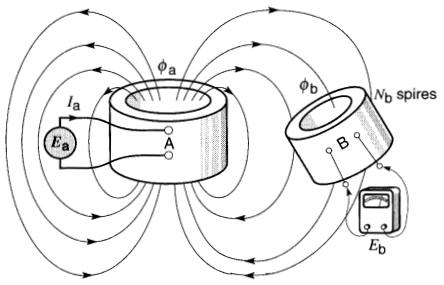
Figure 19-1 La variation de courant dans l'enroulement A induit une tension dans l'enroulement B. C'est le phénomène de inductance mutuelle

La bobine A est parcourue par un courant I, ; elle crée donc un flux θa dont une partie θb «accroche» les spires de la bobine B.

Lorsque le courant Ia varie, le flux θb varie; donc, d'après la loi de Faraday, une tension est induite entre les bornes de la bobine B. La valeur de la tension est donnée par l'équation 18-2, soit :

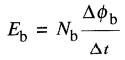    (19-1)

Si le circuit magnétique n'est pas saturé, toute variation de courant ΔIa produit une variation de flux Δθb proportionnelle à ΔIa, ce qui permet d'écrire l'équation:

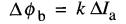    (19-2)

dans laquelle k est un simple facteur de proportionnalité.

En substituant (19-2) dans (19-1) on obtient :

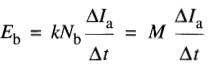
c'est-à-dire

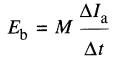    (19-3)

Par définition, le facteur M, nommé inductance mutuelle des deux bobines, donne le rapport entre la tension induite dans une bobine et le taux de variation du courant dans l'autre.

Ce coefficient dépend du nombre de spires des bobines, de leur position relative et des caractéristiques du circuit magnétique qui les relie. L'inductance mutuelle de deux bobines augmente:

(1) si l'on augmente le nombre de spires,

(2) si on les rapproche l'une de l'autre,

ou (3) si on les relie par un noyau magnétique.

L'unité SI d'inductance mutuelle est le henry (symbole H). L'inductance mutuelle de deux bobines est de 1 henry si une variation de courant de 1 ampère par seconde dans l'une induit une tension de 1 volt dans l'autre.

Exemple 19-1

L'inductance mutuelle des enroulements A et B de la Fig. 19-1 est de 3,7 henrys.

Figure 19-1 La variation de courant dans l'enroulement A induit une tension dans l'enroulement B. C'est le phénomène de inductance mutuelle

Quelle est la valeur moyenne de la tension induite dans la bobine B lorsquele courant dans la bobine A, décroît de 7 A à 3 A en 2 secondes ?

Solution

Variation de courant ΔI = (7A - 3A) = 4A

Durée de la variation Δt = 2 s

Inductance mutuelle M = 3,7H

En appliquant la formule 19-3, on trouve:

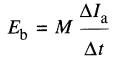
= 3,7 x (4/2) = 7,4V

On remarquera que ce n'est pas le courant dans la bobine A qui engendre une tension dans la bobine B, mais bien la variation de flux (produite par la variation du courant) qui donne naissance à cette tension.

Cependant, en pratique, une formule donnant la tension induite dans une bobine en fonction de la variation du courant dans une autre est plus utile qu'une équation faisant intervenir le flux.

En effet, il est plus facile de mesurer et de suivre les variations d'un courant que les variations d'un flux.

L'inductance mutuelle de deux bobines demeure la même, quelle que soit la bobine qui est alimentée. C'est d'ailleurs une propriété de l'ensemble des deux bobines tout comme leur masse ou leur couleur.

Self-inductance

Considérons la bobine de la Fig. 19-2 portant un courant 1 et produisant un flux θ.

Figure 19-2 La variation du courant I dans la bobine induit une tension entre ses bornes. C'est le phénomène de la self-inductance

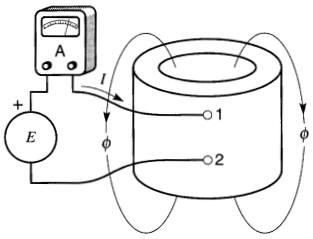
Si le courant varie d'un montant ΔI, cela produira un changement correspondant de flux Δθ.

Cependant, une variation de flux à l'intérieur de la bobine induit une tension entre ses bornes. Nous en venons à la conclusion que le courant variable dans une bobine induit une tension entre ses propres bornes. C'est le phénomène de self-induction.

La tension induite dépend du nombre de spires de la bobine, de sa forme et du taux de variation du courant. Par analogie avec l'induction mutuelle, la valeur de la tension induite est donnée par l'équation:

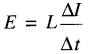    (19-4)

où

E = tension induite, en volts [V]
L = self-inductance de la bobine, en henrys [H]
ΔI = variation du courant, en ampères [A]
Δt = durée de la variation, en secondes [s]

La self-inductance L donne la relation entre la tension induite dans une bobine et le taux de variation du courant qui la parcourt.

Comme pour l'inductance mutuelle, l'unité SI de self-inductance est le henry.

Une bobine possède une self-inductance de 1 henry si une tension de 1 volt est induite lorsque le courant qui la parcourt varie à un taux de 1 ampère par seconde. Notons que le terme self-inductance est habituellement connu sous le nom abrégé d'«inductance».

La Fig. 19-3 montre une inductance de 18 mH pouvant porter un courant de 6400 A.

Figure 19-3 Inductance de lissage de 18 mH, 6400 A. c.c. servant de filtre pour l'alimentation des électro-aimants de guidage du synchrotron à protons du CERN, à Genève. Pesant 35 tonnes et refroidie à l'eau, cette inductance élimine les ondulations du courant pour toute fréquence comprise entre 50 Hz et 3000 Hz

Exemple 19-2

Une bobine ayant une inductance de 2H est parcourue par un courant de 5A lorsqu'elle est raccordée à une pile de 4V (Fig. 19-4).

Figure 19-4

a. Le courant initial dans une bobine est de 5A, la tension à ses bornes est de 4V.

b. Lors de l'ouverture du circuit, le courant diminue rapidement, ce qui induit une tension de 100 V entre les bornes 1 et 2.

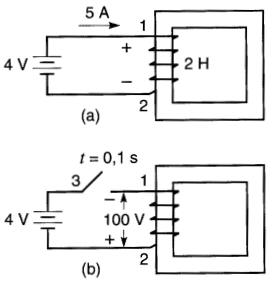
Calculer la valeur moyenne de la tension induite si le courant est interrompu en 0,1 s.

Solution

En appliquant la formule (19-4) on trouve :

E = L (Δi / Δt) = 2 x ((5 - 0) / 0.1) = 100V

On remarque que la tension induite (100 V) est de beaucoup supérieure à la tension de la pile (Fig. 19-4b).

Polarité de la tension induite

La bobine de la Fig. 19-5 est branchée à une source de courant G qui lui fournit un courant I. Supposons que la résistance de l'enroulement soit rigoureusement nulle; il n'y aura donc aucune chute de tension et aucune perte Joule.

Dans l'analyse qui suit nous étudierons ce circuit pour trois conditions différentes :

a) le courant ne varie pas

b) le courant augmente

c) le courant diminue

Si le courant est constant, le flux est constant et aucune tension n'est induite (Fig. 19-5a).

Figure 19-5a Lorsque le courant ne varie pas, la tension entre les bornes est nulle.

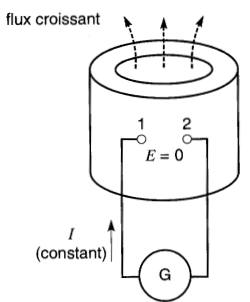
Puisqu'il n'y a aucune chute de tension RI due à la résistance, la tension E aux bornes de l'enroulement est nulle. Lorsque le courant augmente (Fig. 19-5b), le flux augmente et une tension E est induite.

Figure 19-5b Lorsque le courant augmente, une tension est induite et la borne 1 est positive. La bobine agit comme une charge

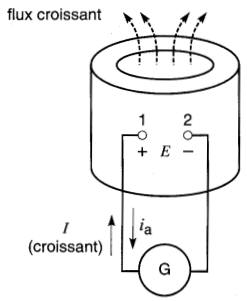
Elle apparaît aux bornes de la bobine. D'après la loi de Lenz, la polarité de cette tension est telle qu'elle tend à s'opposer à la croissance du flux. donc à la croissance du courant I.

Par conséquent, si la tension induite agissait seule, elle produirait un courant i a opposé au courant I. Cela veut dire qu'à l'intérieur de la bobine, ia se dirigerait vers la borne 1. Par conséquent, la borne 1 est (+) par rapport à la borne 2. La tension E12 est donc positive (+).

Lorsque le courant diminue (Fig. 19-5c), le flux diminue et un flux croissant induite et une tension E12 est encore induite. La polarité de cette tension est telle qu'elle tend à s'opposer à la décroissance du courant I.

Figure 19-5c Lorsque le courant diminue, une tension est induite et la borne 1 est négative. La bobine agit comme une source

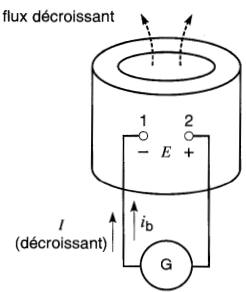
Par conséquent, si la tenon induite agissait seule, elle produirait un courant ib, dans le même sens que I. Afin de produire un tel cousant. il faut que la borne 2 soit (+) par rapport à 1. La tension E12 est donc négative (-).

En comparant les Fig. 19-5b et 19-5c, on constate que la polarité de la tension induite ne dépend pas du sens du courant I, mais de la façon dont il varie.

De plus, la tension induite tend à s'opposer au changement de courant dans la bobine. Il est important de réaliser que le vrai courant circulant dans le circuit est I; les courants ia et ib, sont des courants fictifs utilisés comme artifices pour déterminer la polarité de la tension E12 induite.

La polarité de la tension induite dans une bobine couplée à une autre peut être établie en suivant le raisonnement de l'exemple 18-2 de la section précédent Induction électromagnétique.

Énergie emmagasinée dans le champ magnétique d'une bobine

La polarité en soi n'a pas grand intérêt, mais si on l'associe à la direction du courant I, elle nous conduit à une découverte importante.

Ainsi, la Fig. 19-5b indique que lorsque le courant I augmente, il entre par une borne positive. La bobine se comporte donc comme une charge, absorbant une puissance instantanée de El watts pendant un certain temps.

Qu'arrive-t-il de cette énergie?

Puisque la bobine ne possède aucune résistance, l'énergie n'est pas dissipée sous forme de chaleur. Puisque le montage est immobile. i l n'y a aucune dépense d'énergie mécanique.

On conclut que l'énergie est emmagasinée dans le champ magnétique de la bobine, un peu comme on emmagasine de l'énergie mécanique lorsque l'on comprime un ressort. Dans le cas de la Fig. 19-5c, on constate que lorsque le courant I décroît, il sort par la borne positive.

La bobine se comporte alors comme une source fournissant de l'énergie au reste du circuit. Cette énergie provient du champ magnétique qui doit, par conséquent, décroître. Un enroulement peut donc emmagasiner et restituer de l'énergie comme le fait une batterie de piles. L'énergie est conservée dans le champ magnétique et elle augmente et diminue avec celui-ci.

L'énergie W conservée dans le champ magnétique est donnée par l'équation:

W = (LI²)/2    (19-5)

où

W = énergie dans le champ [J]
L = inductance de la bobine [H]
I = courant dans la bobine [A]

Exemple 19-3

Une bobine possédant une self-inductance de 4 H est traversée par un courant de 40A (Fig. 19-6a).

Figure 19-6a Voir exemple 19-3

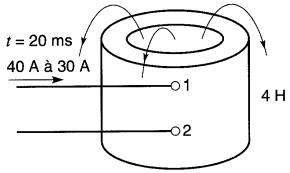
Calculer:

a) la valeur de l'énergie emmagasinée dans le champ magnétique:

b) l'énergie débitée par la bobine si le courant diminue de 40A à 30A:

c) la tension induite aux bornes de la bobine ainsi que la puissance débitée si cette diminution de 40,3% à 30A se fait uniformément en 20 millisecondes.

Solution

a) Pour un courant de 40A, l'énergie conservée dans le champ vaut:

W1 = 1/2 LI² = 1/2 x 4 x 40² = 3200J

b) Lorsque le courant tombe à 30A, l'énergie conservée dans le champ devient:

W2 =1/2 LI² =1/2 x 4 x 30² =1800J

La bobine a donc débité une énergie de:

W = W1 - W2 = 3200 -1800 = 1400J

Cette énergie est retournée au circuit sur lequel la bobine est branchée.

c) La tension induite aux bornes est:

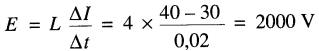
La puissance moyenne débitée par la bobine est :

P = énergie/temps = 1400J / 0,02s = 70 000 W = 70 kW

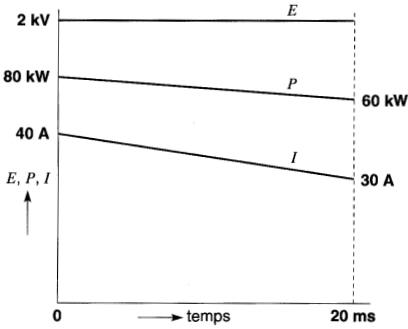
Les valeurs de E, I et P en fonction du temps sont montrées à la Fig. 19-6b.

Figure 19-6b Tension, puissance et courant en fonction du temps, lorsque le courant diminue linéairement de 40A à 30A.
Voir exemple 19-3

Mise sous tension d'un circuit inductif

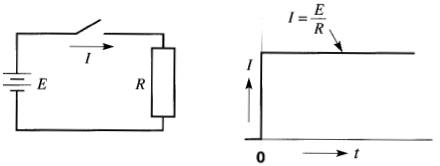
Lorsqu'on applique une tension E sur une résistance R, le courant monte immédiatement à une valeur:

I = E / R

conformément à la loi d'Ohm.

La Fig. 19-7 montre le circuit et le graphique du courant en fonction du temps.

Figure 19-7 Graphique du courant dans une résistance en fonction du Temps lorsque l'interrupteur est fermé à t = 0

Qu'arrive-t-il lorsqu'on applique une tension constante E sur une bobine ayant une inductance L et une résistance nulle?

D'après l'équation 19-4 on a :

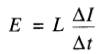
d'où

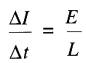    (19-6)

Comme E et L sont des constantes, l'équation (19-6) révèle que le taux de variation du courant est constant et égal à E/L. La Fig. 19-8 montre que le courant augmente uniformément avec le temps, à partir de l'instant de fermeture du circuit.

Figure 19-8 Graphique du courant dans une inductance (bobine ou spire) enfonction du temps, lorsque l'interrupteur est fermé à t = 0

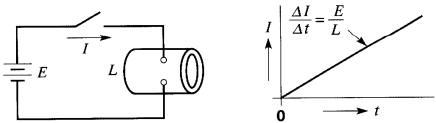
 Contrairement à une résistance, le courant ne plafonne pas et il augmente théoriquement sans limite. Cependant, en pratique, le courant ne peut pas augmenter indéfiniment car il y a une limite à ce que la source peut fournir.

Notons que si l'inductance était 10 fois plus grande, le taux de croissance du courant serait 10 fois plus petit. Par conséquent, le courant augmenterait 10 fois moins vite.

Exemple 19-4

Une bobine avant une résistance négligeable possède une inductance de 4H.

Déterminer la courbe du courant en fonction du temps si la bobine est branchée sur une source de 12V.

Combien de temps est requis pour atteindre un courant de 27A?

Solution Le taux de variation du courant est :

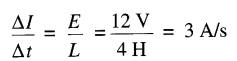
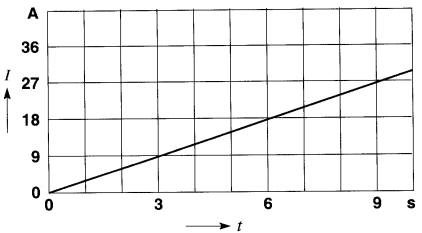
Le courant augmente à raison de 3 A/s (Fig. 19-9). Le temps requis pour atteindre 27A est de 9s.

Figure 19-9 Voir exemple 19-4.

Constante de temps

En pratique, une bobine possède toujours une résistance R et une inductance L. Supposons qu'on la branche sur une source de tension E.

Si la résistance agissait seule, on obtiendrait la courbe 1, soit I = E/R (Fig. 19-10). De même, si l'inductance agissait seule, on obtiendrait la courbe 2, soit ΔI/Δt = EIL.

Figure 19-10 Pour une bobine ayant une résistance R et une inductance L, la courbe 3 décrit la variation du courant en fonction du temps. Le temps lest la constante de temps de la bobine

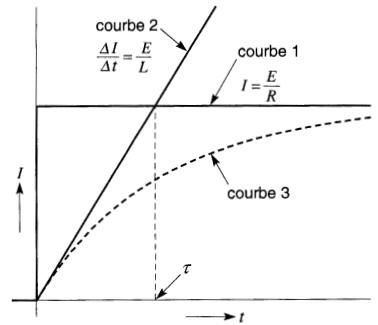
La véritable courbe 3 du courant en fonction du temps suit une trace qui est asymptotique aux courbes 1 et 2.

La courbe 3 possède une forme dite exponentielle, forme que nous discuterons à la section suivante. La courbe exponentielle possède une caractéristique appelée constante de temps τ. τ est une lettre grecque qui se prononce «tau»

La constante de temps fournit une mesure du temps requis pour qu'une grandeur comme, dans notre cas, le courant I, atteigne sa valeur finale.

On peut démontrer que la valeur de τ est égale au temps requis pour atteindre la valeur finale de I si le courant augmentait au taux déterminé par l'inductance seule. La constante de temps correspond donc au point d'intersection des courbes 1 et 2. Il s'ensuit que la valeur de test donnée par l'expression:

 τ = L / R     (19-7)

ou 2 = constante de temps de la bobine ou du circuit [s]

L = inductance de la bobine ou du circuit [H]

R = résistance de la bobine ou du circuit [Ω]

Exemple 19-5

Une bobine ayant une résistance de 1Ω et une inductance de 4H est connectée à une source à c.c. de 12 V (Fig. 19-11).

Figure 19-11 Voir exemple 19-5

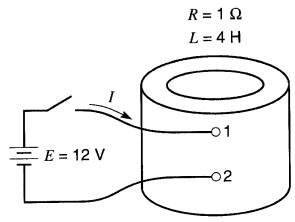
Calculer:

a) La valeur finale du courant

b) La constante de temps de la bobine

c) Les tensions, et ΔI/Δt au moment de la fermeture de l'interrupteur

d) Les tensions et ΔI/Δt lorsque le courant a atteint 8A

Solution

a) La valeur finale du courant est : 

I = E/R = 12V / 1Ω = 12A

Lorsque le courant a atteint sa valeur finale, le flux ne change plus et la tension induite devient nulle.

Le temps requis pour atteindre la valeur finale dépend de l'inductance et de la résistance de la bobine : plus l'inductance est grande et plus la résistance est faible, plus le courant prend de temps à atteindre sa valeur finale.

b) La constante de temps est :

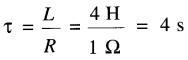
c) Le circuit de la Fig. 19-12 montre séparément la résistance et l'inductance de la bobine.

Figure 19-12 Circuit électrique équivalent au montage de la Fig. 19-11, montrant les composants R et L d'une bobine et la tension aux «bornes» de chaque élément

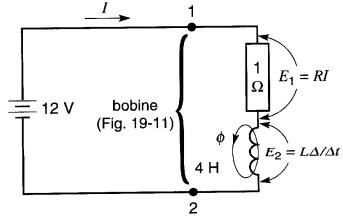
Cela permet d'analyser le courant et les tensions dans le circuit.

La tension de 12 V aux bornes de la bobine est composée de deux tensions : la chute E1 = RI dans la résistance R et la tension induite E2 = L ΔI/Δt. La tension E1 dépend de la valeur du courant I tandis que E2 dépend de son taux de variation.

Au moment de la fermeture, le courant est nul, mais il change rapidement:

E1 = 0 et E2 = 12 V.

Le taux de changement du courant à cet instant est:

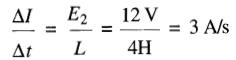
d) Lorsque le courant atteint 8A, on a E1 = 8 V. Il s'ensuit que E2 = 4 V, car la somme (E1 + E2) doit rester égale à la tension de la source (12V). Le taux de changement du courant à cet instant est:

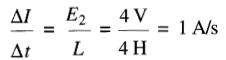
 Forme de la courbe exponentielle

L'lorsqu'une grandeur Q (comme un courant ou une tension) suit une courbe exponentielle, sa variation en fonction du temps suit un trajet bien défini.

L'expression est donnée par la formule :

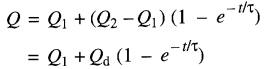    (19-8)

où

Q = valeur de la grandeur au temps t

Q₁ = valeur initiale de la grandeur

Q₂ = valeur finale de la grandeur

Q_d = Q₂-Q₁

t = temps écoulé [s]

τ = constante de temps [s]

e = base logarithmique (valeur = 2,718...)

Cette formule permet de tracer toute courbe exponentielle à l'aide d'une calculatrice de poche.

Il est encore plus facile de tracer cette courbe en faisant appel à une grandeur dérivée de la constante de temps τ et appelée demi-temps T₀.

La relation entre T₀ et la constante de temps τ est donnée par l'expression:

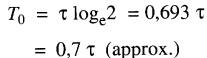    (19-9)

En utilisant le demi-temps T₀, on peut alors dresser un tableau universel donnant les valeurs de Q à des intervalles distincts, multiples de T₀. Ces valeurs sont présentées au tableau 19-1.

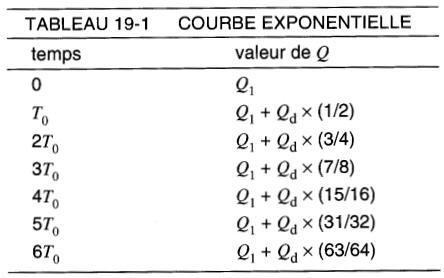
En observant les valeurs successives du tableau 19-1, on notera qu'à chaque intervalle T₀ la quantité Q augmente d'une valeur qui est la moitié de celle obtenue à l'intervalle précédent. C'est pourquoi T₀ s'appelle le demi-temps.

On constate qu'après une période 6T₀ la valeur de Q est (63/64) de Q2 ou 98,4 % de sa valeur finale. À toutes fins utiles, on peut considérer que c'est la valeur finale.

Noter que 6T₀correspond à 4,2τ, soit environ 4 constantes de temps.

Exemple 19-6

Tracer la courbe du courant en fonction du temps pour la bobine de l'exemple 19-5, sachant que le courant initial est nul.

Solution

D'après la solution de l'exemple 19-5, on sait que Q₁=0A, Q₂=12A, τ=4s et Qd=(12-0)=12A.

Il s'ensuit que:

T₀ = 0,7τ  = 0,7 x 4 = 2,8s

Les valeurs du temps t et du courant correspondant sont choisies conformément au tableau 19-1, ce qui donne le tableau 19-2.

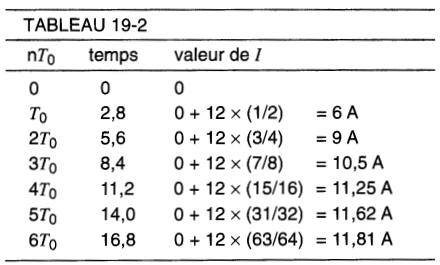
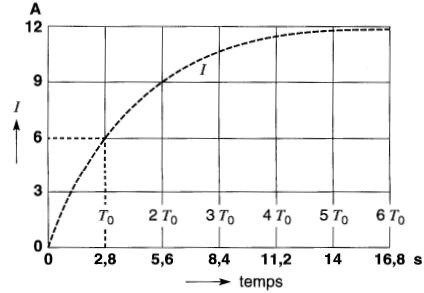
La courbe du courant en fonction du temps est montrée à la Fig . 19-13.

Figure 19-13 Courbe du courant en fonction du temps pour le circuit de la Fig. 19-11

Ouverture d'un circuit inductif

Considérons une bobine d'inductance L, alimentée de- puis un certain temps par une source de tension El (Fig. 19-14).

Figure 19-14 Avec un courant constant, l'énergie emmagasinée dans le champ demeure constante

Le courant I circulant dans la bobine est constant et l'énergie emmagasinée dans le champ vaut alors (t1/2)LI² joules. La borne A est positive par rapport à la borne B.

Si l'on ouvre l'interrupteur, le courant et le flux bais- sent brusquement, induisant ainsi une tension élevée E₂ de polarité inverse entre les bornes de la bobine (Fig. 19-15).

Figure 19-15 En ouvrant le circuit, l'énergie emmagasinée dans le champ est dissipée dans l'arc. Noter que la polarité des bornes A, B est l'inverse de celle de la figure 19-14

En tenant compte des polarités, on constate que la tension aux bornes de l'interrupteur est la somme de la tension induite et de celle de la source. Cette tension est tellement élevée qu'elle réussit à créer un arc à travers l'air séparant la lame des contacts fixes de l'interrupteur. Le courant continue donc à circuler à travers l'arc tout en diminuant graduellement.

Finalement, il devient trop petit pour maintenir l'arc et c'est seulement à ce mo- ment que le circuit entre la source et la bobine est réellement ouvert.

Pendant la décroissance du courant, la bobine se comporte comme une source, et l'énergie qu'elle débite est dissipée dans la résistance de l'arc.

Lors de l'ouverture de l'interrupteur toute l'énergie emmagasinée dans le champ doit donc être dissipée dans l'arc. L'ouverture des gros enroulements à courant continu peut créer un arc assez intense pour faire fondre les contacts de l'interrupteur. On devra donc prendre des précautions particulières lors de l'ouverture d'un circuit qui contient un enroulement.

En effet, la tension induite au moment de l'ouverture du circuit peut atteindre plusieurs milliers de volts . Cette tension pourrait causer une rupture de l'isolation sur l'enroulement, ou même donner un choc électrique fatal . De plus, l'arc abîme les contacts de l'interrupteur .

Le problème de la self-induction est particulièrement grave dans les circuits de commande où des relais électromagnétiques sont alimentés et désalimentés plusieurs milliers de fois par jour. L'arc créé lors de la séparation des contacts doit être réduit par des méthodes spéciales que nous allons maintenant décrire.

Méthodes de suppression des arcs

On peut réduire la tension aux bornes de la bobine et l'intensité de l'arc en plaçant une résistance R₀ en parallèle avec la bobine (Fig . 19-16).

Figure 19-16 Une résistance placée aux bornes de la bobine absorbe une partie de l'énergie du champ magnétique

L'énergie dans le champ est alors dissipée surtout dans la résistance et plus faiblement dans l'arc d'ouverture . Plus la résistance est basse, mieux on réussit à étouffer l'arc.

Mais une faible résistance possède l'inconvénient de dissiper une puissance considérable lors du fonctionnement normal de l'enroulement. On arrive à un compromis acceptable en utilisant une résistance R₀ ayant environ 3 fois la résistance de la bobine.

La solution idéale est d'employer une résistance non linéaire, comme un varistor, dont la résistance diminue brusquement lorsque la tension augmente.

Une autre méthode particulièrement efficace consiste à placer une diode en série avec la résistance R₀ en avant soin de la raccorder comme indiqué sur la Fig . 19-17.

Figure 19-17 L'ajout d'une diode isole la résistance, sauf lors de l'ouverture du circuit

La résistance ne dissipe aucune puissance lors- que l'interrupteur est fermé, mais dès son ouverture, la polarité inverse aux bornes de la bobine permet à la diode de conduire.

Si l'on utilise une diode, on peut réduire la résistance R₀ à zéro, évitant ainsi tout arc lors de l'ouverture de l'interrupteur.

 Cependant, le flux créé par la bobine décroît alors très lentement avec une constante de temps τ =L/R, où L est l'inductance de la bobine et R sa résistance. Cela peut présenter un inconvénient, car s'il s'agit d'une bobine de relais, ce dernier ne réagira pas immédiatement après l'ouverture de l'interrupteur.

On peut aussi réduire l'arc en plaçant un condensateur et une résistance R1 aux bornes de l'interrupteur (Fig. 19-18).

Figure 19-18 Condensateur et résistance pour supprimer les arcs lors de l'ouverture du circuit

Lors de l'ouverture de l'interrupteur, le condensateur emmagasine une partie de l'énergie subitement libérée par l'inductance.

 Cette énergie est ensuite lentement dissipée dans le circuit formé par la bobine, le condensateur, la source et la résistance totale du circuit.

Lorsque l'interrupteur est ouvert, le condensateur demeure chargé à la tension de la source. Le but de la résistance R1 est de limiter le courant de décharge lorsque l'interrupteur est refermé, afin de ne pas abîmer ses contacts.

Exemple 19-7

La bobine de la Fig. 19-17 possède une inductance de 12H et une résistance de 35Ω. Elle est alimentée par une source de 24 V. Afin d'éliminer l'arc lors de l'ouverture de l'interrupteur, on place aux bornes A, B une résistance R₀ de 175Ω en série avec une diode.

Déterminer la forme d'onde de la tension aux bornes de la bobine à la suite de l'ouverture du circuit.

Solution

Avant l'ouverture du circuit, le courant dans la bobine est I = 24 V/35Ω = 0,686A.

Au moment de l'ouverture, ce courant demeure inchangé, à cause de l'inductance de la bobine. Comme l'arc est supprimé, le courant doit circuler dans R₀ et la diode. La chute de tension dans la diode étant négligeable, la tension E_AB entre les bornes A et B change subitement de signe et passe de +24V à E_AB = - 0,686A x 175Ω = -120V, soit E_BA= +120V.

La résistance du circuit est maintenant 175 + 35 = 210Ω, alors que son inductance est toujours 12H.

La constante de temps est donc:

τ = L/R = 12H / 210Ω = 0,0571s = 57,1 ms.

Cela correspond à un demi-temps de T₀ = 0,7 x 57,1 = 40ms

Le courant dans la bobine, de même que la tension a ses bornes, décroissent exponentionnellement jusqu'à zéro.

On peut alors tracer la courbe de décharge de E_BA en utilisant le tableau 19-1.

Dans cet exemple, Q1 = 120 V et Q2= O V, donc Qd = Q2-Q1 = -120V

Les valeurs de la tension aux bornes de la bobine en fonction du temps sont présentées au tableau 19-3. La courbe de décroissance de E_AB est montrée à la Fig. 19-19.

Figure 19-19 Courbe E_BA en fonction du temps. Voir exemple 19-7 et Fig. 19-17

Détermination graphique du courant dans une inductance

Nous avons vu à la section 19.2 qu'il existe à chaque instant une relation entre la tension aux bornes d'une inductance et le taux de variation du courant qui la parcourt.

Cette relation est donnée par l'expression (19-4), soit: 

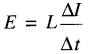
Cette formule permet de calculer facilement la valeur de la tension E lorsqu'on connaît la forme d'onde du courant.

Cependant, il arrive souvent que la tension E aux bornes d'une inductance soit imposée et qu'on veuille calculer la valeur du courant résultant. Dans ces circonstances, à moins d'employer des mathématiques avancées, il est difficile de calculer la valeur du courant en utilisant directement la formule:

Nous utiliserons plutôt une méthode graphique appelée méthode des volts-secondes. Pour utiliser cette méthode, il s'agit de transposer l'expression ci-dessus, en la mettant sous la forme:

(19-4a)

Comment interpréter cette nouvelle expression?

Elle nous indique que si une tension E existe aux bornes d'une inductance L durant un intervalle Δt, le courant qu'elle porte variera de ΔI.

Le changement sera d'autant plus grand que l'inductance L est petite.

Par exemple, supposons que la tension aux bornes d'une bobine soit de 40V durant un intervalle de 72ms, et que l'inductance de la bobine soit de 1,2H .

Durant cet intervalle, le changement de courant ΔI sera:

ΔI = (EΔT) / L = (40 x 0,072) / 1,2 = 2,4A

Le courant augmentera ou diminuera selon que la tension E est positive ou négative. Lorsqu'une tension varie en fonction du temps pendant une certaine période, on doit subdiviser la période en intervalles très courts. Cela permet, en effet, de garantir que la tension E reste pratiquement constante durant chaque intervalle.

Ensuite, on calcule le changement de courant durant chaque intervalle. Connaissant la valeur initiale du courant, on peut alors, en répétant le calcul de ΔI, trouver la valeur du courant tout au long de la période.

On remarquera que le produit EΔt représente la petite surface, en volts-secondes, située en dessous de la tension E durant le court intervalle Δt.

Par conséquent, afin de trouver le courant circulant dans une inductance après une période T appréciable, il faut déterminer les surfaces comprises en dessous de la courbe de tension E pendant cette période.

Les surfaces sont mesurées en volts-secondes ; elles sont positives lorsque la tension est positive et négatives lorsque la tension est négative. La surface nette après un temps T s'obtient en soustrayant les surfaces négatives des surfaces positives.

Supposons, par exemple, que la tension aux bornes dune inductance suive la courbe de la Fig. 19-20.

Figure 19-20 Courbe montrant la tension aux bornes d'une inductance (bobine) en fonction du temps

Durant la période T, la surface A1 en dessous de la courbe est positive tandis que la surface A2 est négative. Il s'ensuit que A, la surface nette à la fin du temps T est égale à (A1 -A2) volts-secondes.

Si le courant initial est zéro, sa valeur I au bout du temps Test donnée par l'expression :

I = A/L    (19-10)

où

I = courant dans l'enroulement après un temps T, en ampères [A]

A = surface nette en dessous de la courbe de tension pendant le temps T, en volts-secondes [V.s]

L = inductance de l'enroulement, en henrys [H]

Considérons un enroulement ayant une inductance L et une résistance négligeable. La tension à ses bornes varie selon la courbe de la Fig. 19-21. Si le courant initial est nul, sa valeur à l'instant t1 sera:

Figure 19-21 Méthode des volts-secondes pour calculer le courant dans un enroulement

I = A1 / L

À mesure que le temps s'écoule, la surface augmente progressivement; par conséquent, le courant continue à croître. Il atteint sa valeur maximale à l'instant t2 car c est à ce moment que la surface comprise sous la courbe de tension cesse d'augmenter (Fig. 19-22).

Figure 19-22 Forme d'onde du courant dans l'enroulement

Après t2, la tension devient négative et, par conséquent, la surface nette commence à diminuer. À l'instant t3, par exemple, la surface nette est égale à (A1 + A2 - A3) et le courant correspondant est:

I= (A1 +A2 -A3) / L

À l'instant t4, la surface négative (A3 + A4) est égale à la surface positive (A1 + A2). Par conséquent, la surface nette est nulle et le courant redevient nul, comme il l'était à t = 0.

Après l'instant t4, le courant devient négatif, c'est-à-dire qu'il change de sens (Fig. 19-21 et 19-22).

Note importante: si le courant initial (t = 0) est I₀ au lieu de zéro, il suffit d'ajouter I₀ à chacune des valeurs calculées selon la méthode des volts-secondes.

Exemple 19-8

La tension E aux bornes d'une bobine de 2 H suit la courbe donnée à la Fig . 19-23.

Figure 19-23 Voir exemple 19-8

Sa résistance est négligeable.

Déterminer la valeur du courant instantané I dans le circuit, sachant que le courant initial est nul.

Solution

Intervalle de 0 à 3 secondes :

pendant cet intervalle, la tension de 4V aux bornes est constante. Donc, la surface en volts-secondes augmente uniformément et linéairement.

Ainsi, après 1 seconde la surface est de 4 V•s, après 2 secondes elle est de 8 V•s, après 3 s, de 12 V•s .

Le courant I est donné par la relation I = A/L, où L = 2H; le courant prend donc les valeurs respectives de 2A, 4A, etc ., pour atteindre 6A après 3 secondes.

Intervalle de 3 à 5 secondes:

la tension baisse subitement à 2V durant 2s.

La surface continue à augmenter mais à un taux moins rapide, car la tension E est plus petite qu'auparavant.

Lorsque t =5 s, la surface totale en dessous de la courbe depuis le début est de 16 V•s ; par conséquent, le courant

I = A/L = 16 V•s / 2H = 8A.

Intervalle de 5 à 7 secondes:

pendant cette période la tension augmente de 2V à 6V.

La surface augmente de 4 carreaux, ce qui équivaut à 8 V•s, donc à une augmentation de courant de 4A.

Le courant à t = 7s est donc 8A + 4A =12A.

Remarquer que la courbe du courant n'est pas une droite pendant cet intervalle, car la tension n'est pas constante.

Intervalle de 7 à 8 secondes:

la tension change subitement de polarité, passant de 6V à - 8V, de sorte que les 8 V•s compris dans cet intervalle se soustraient des volts-secondes accumulés précédemment.

La surface nette depuis le début est donc 24 V•s - 8 V•s = 16 V•s.

Par conséquent, le courant à la fin de cet intervalle (t = 8 s) est: I=16V•s / 2H= 8A.

Intervalle de 8 à 10 secondes:

la tension est nulle aux bornes de l'inductance. La surface nette demeure inchangée; par conséquent, le courant ne change pas, mais reste à 8A.

Intervalle de 10 à 14 secondes: la tension est - 4V et les volts-secondes négatifs continuent à s'accumuler.

À t = 14 s, l'ensemble des surfaces négatives est égale à l'ensemble des surfaces positives, de sorte que le courant redevient nul.

Passé cet instant, le courant change de sens.

Si le courant avait eu une valeur initiale, disons, de +7A, on devrait ajouter cette valeur à chacun des courants calculés ci-dessus.

Pour obtenir la nouvelle courbe de courant, il suffirait de décaler la courbe de la Fig. 19-23 de 7A vers le haut. Ainsi, le courant à t = 7s serait 12 + 7 = 19A.

FORMULES POUR CALCUL D'INDUCTANCES

Le calcul de l'inductance pour certains enroulements et pour certaines formes de conducteurs est particulièrement utile. Les formules données dans les exemples qui suivent sont approximatives, mais suffisamment précises pour les applications pratiques .

Bobine à noyau de fer ayant un entrefer

L'inductance de ce type de bobine (Fig . 19-24) dépend surtout des dimensions de l'entrefer, le noyau de fer ne servant qu'à canaliser le flux.

Figure 19-24

Pour un noyau de fer très perméable, l'inductance est donnée par la formule :

    (19-11)

où

L = inductance, en microhenrys [gH]
N = nombre de spires de la bobine
A = surface de l'entrefer, en mètres carrés [m 2]
= longueur de l'entrefer, en mètres [m]

Exemple 19-9

Dans la Fig. 19-24, si N = 1000 spires, A = 4 cm x 1,5 cm, = 1 mm, on obtient :

Bobine toroïdale à noyau d'air Une bobine toroïdale (Fig . 19-25) possède l'avantage de ne créer aucun flux à l'extérieur de ses spires.

Figure 19-25

Lorsque les spires sont réparties uniformément, la bobine possède une inductance donnée par la formule :

    (19-12)

où

L = inductance, en microhenrys [µH]
N = nombre de spires
a = diamètre extérieur, en mètres [m]
b = diamètre intérieur, en mètres [ml

Exemple 19-10

Dans la Fig. 19-2 si N = 1000, a = 40 cm, b = 30 cm, on obtient :

 Bobine à noyau d'air

Les bobines droites (Fig. 19-26) sont très répandues dans les circuits à basses et à hautes fréquences.

Figure 19-26

L'inductance de ces bobines est donnée par la formule :

    (19-13)

ou

L = inductance, en microhenrys [µH]
N = nombre de spires
d = diamètre moyen, en mètres [ml
l = longueur, en mètres [m]

Note: Si l/d > 0,2, la précision de la formule est plus petite que ± 3 %.

Exemple 19-11

Dans la Fig. 19-26, si N = 1000, d = 40 cm, 1 = 20 cm, on obtient:

Rouleau de fil à noyau d'air

Bien que ce type de bobine (Fig. 19-27) soit peu utilisé (elle est utilisée dans les radios voir Barre d'antenne AM, Air coil inductor), la formule suivante permet de déterminer l'inductance approximative des bobines courtes ayant un grand diamètre.

    (19-14)

Figure 19-27

où

L = inductance, en microhenrys[µH]

N = nombre de spires

D = diamètre moyen, en mètres [m]

d = diamètre du faisceau de spires [m]

Exemple 19-12

Dans la Fig. 19-27, si N= 1000, D = 40 cm, d = 2,5 cn1, on a:

eux conducteurs parallèles Deux conducteurs longs et parallèles (Fig . 19-28) forment une grande spire possédant une inductance appréciable.

Figure 19-28

Cette inductance joue un rôle important dans les lignes de transport de l'énergie électrique.

L'inductance est donnée par la formule :

     (19-15)

où

L = inductance, en microhenrys [µH]
l = longueur des conducteurs, en mètres [m]
D = distance séparant les centres, en mètres [m]
d = diamètre des conducteurs, en mètres [m]

Exemple 19-13

Dans la Fig. 19-28, si l = 10 km, D = 3 m, d = 25 mm, on a:

Deux barres omnibus parallèles

Tout comme deux conducteurs circulaires, deux barres omnibus (Fig. 19-29) forment une spire dont l'inductance est donnée par la formule:

     (19-16)

Figure 19-29

où

L = inductance, en microhenrys [µH]
l = longueur des barres, en mètres [m]
D = distance entre les centres, en mètres [m]
a = largeur d'une barre, en mètres [m]
b = épaisseur d'une barre, en mètres [m]

Note: Cette formule donne une précision plus petite que ± 2 % si: D > (a+b) / 2 et l > 60D

Exemple 19-14