Ellipse approximative à quatre centres

Une ellipse approximative est, en général, suffisamment précise pour représenter un cercle en perspective isométrique. Le tracé couramment utilisé est celui d'une ellipse à quatre centres, il est illustré aux figures 16.24, 16.25 et 16.26. Cette méthode n'est applicable qu'aux ellipses situées sur les plans isométriques.

Figure 16.24
Construction d'une ellipse à quatre centres

Figure 16.25
Dessin isométrique d'un palier

Figure 16.26
Ellipses à quatre centres

A partir d'un cercle donné dans une vue en projection à vues multiples, la méthode consiste à tracer, ou simplement à imaginer, un carré circonscrit à ce cercle. Ensuite, on procède en suivant les étapes illustrées à la figure 16.24.

I. Dessinez la perspective isométrique du carré, elle est un losange dont chaque côté est égal au diamètre du cercle considéré.

II. Tracez, à l'aide d'une équerre à 60°, les médiatrices des quatres côtés du losange. Leurs quatres points d'intersection constituent les quatre centres de cercle. On remarque que deux centres coïncident nécessairement avec les deux sommets opposés du losange.

III. Tracez deux grands arcs de cercle de rayon R.

IV. Tracez deux petits arcs de cercle de rayon r, ce qui complète l'ellipse approximative. On remarque que les centres de ces petits arcs de cercle doivent se trouver sur la diagonale horizontale du losange et que les quatre arcs de cercle doivent être tangents aux côtés du losange, à leur milieu.

Une application de cette méthode de construction est illustrée à la figure 16.25. On note que les quatre centres de la grande ellipse ne sont pas les mêmes que ceux de la petite,
même si les deux ellipses représentent deux cercles concentriques.

Chaque ellipse a son propre losange et ses propres centres. Pour tracer l'ellipse à la base du cylindre, il suffit de translater verticalement les centres de l'ellipse supérieure d'une distance égale à la hauteur c du cylindre.

La figure 16.26 illustre trois ellipses à quatre centres situées sur les trois faces visibles d'un cube. On constate que le dessin entier peut être exécuté à l'aide d'un té, d'une équerre à 60° et d'un compas.

La différence entre une ellipse à quatre centres et une ellipse exacte est illustrée à la figure 16.27.a.

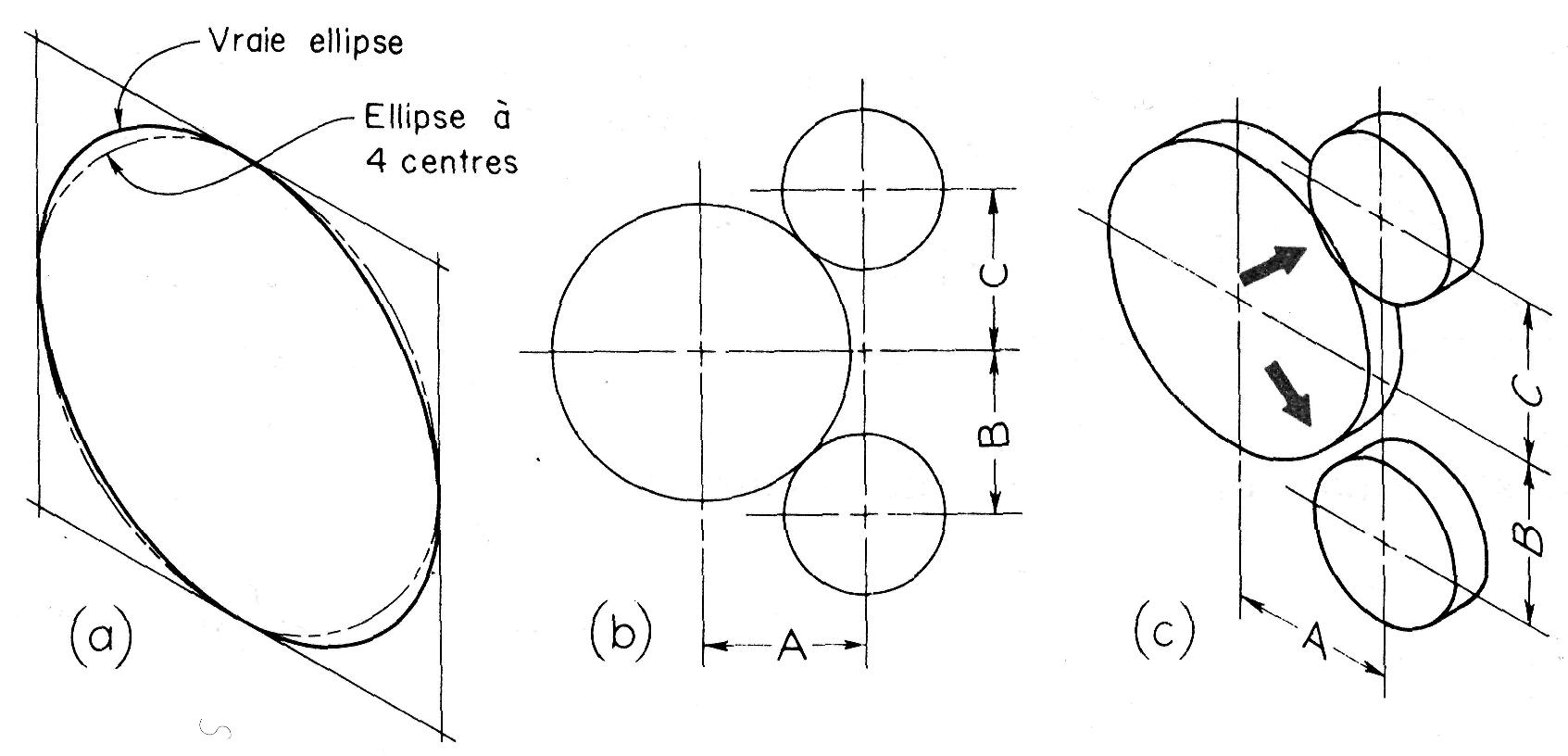
Figure 16.27
Défauts d'une ellipse à quatre centres

L'ellipse à quatre centres est moins « plate » et plus courte que la vraie ellipse. Pour cette raison, lorsque l'on doit représenter des cercles tangents, tels que ceux en (b), en perspective isométrique, les ellipses à quatre centres deviennent peu satisfaisantes (c).

Pour obtenir une meilleure approximation de l'ellipse exacte, on peut utiliser la méthode
suggérée par le professeur Orth (figure 16.28). La construction ne requiert qu'une seule étape supplémentaire, mais la précision obtenue est suffisante pour pratiquement tous les cas.

Figure 16.28
Ellipse à quatre centres d'Orth

Lorsque l'on veut tracer une ellipse à quatre centres à partir des axes plutôt que du losange circonscrit, on utilise la méthode illustrée à la figure 16.29. L'ellipse obtenue à la dernière étape (III) est identique à celle tracée selon la première méthode (figures 16.24 et 16.26).

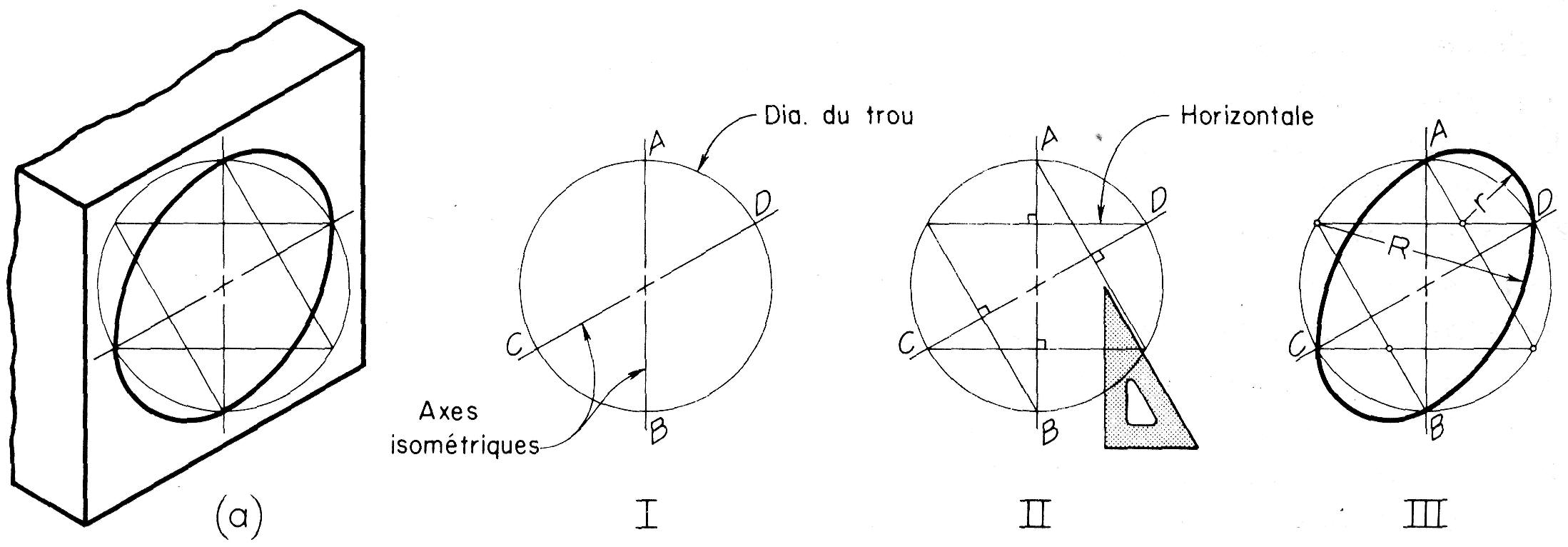
Figure 16.29
Ellipse à quatre centres construite à partir des axes isométriques